Файл: Методические рекомендации по выполнению контрольной работы по дисциплине Математика.docx
Добавлен: 03.12.2023
Просмотров: 138
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
;
– вероятность того, что в п испытаниях событие A наступит не более m раз
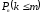 =
=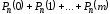 .
.
– вероятность того, что в п испытаниях событие A наступит не менее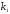 и не более
и не более 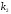 раз
раз
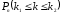 =
=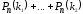 .
.
Все эти вероятности могут быть вычислены по формуле Бернулли, однако, на практике ввиду вычислительных сложностей это возможно лишь при небольших n и поэтому используются приближенные формулы.
2.1. Локальная теорема Лапласа
Если число испытаний n велико, а вероятность p не очень мала, то
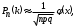
где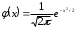 ,
, 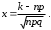
Значения функции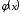 приведены в приложении (таблица 1), при
приведены в приложении (таблица 1), при 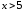 полагают
полагают 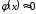 , для отрицательных значений x пользуются тем, что функция
, для отрицательных значений x пользуются тем, что функция 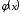 четная, и, следовательно,
четная, и, следовательно, 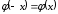 .
.
2.2. Интегральная теорема Лапласа
Вероятность того, что событие А появится в n испытаниях не менее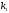 и не более
и не более 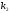 раз находится по формуле
раз находится по формуле
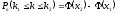 ,
,
где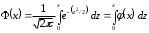 ,
, 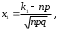
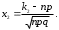
Значения функции Лапласа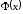
приведены в приложении (таблица 2), при полагают
полагают 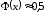 , для отрицательных значений x пользуются тем, что функция
, для отрицательных значений x пользуются тем, что функция  нечетная, и, следовательно,
нечетная, и, следовательно, 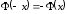 .
.
Если число испытаний n велико, а вероятность p появления события в каждом испытании очень мала, то
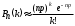 .
.
Обозначив , =np– среднее число успехов в серии испытаний, получим
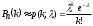 .
.
Значение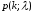 по заданным k и можно определить по приложению (таблица 3).
по заданным k и можно определить по приложению (таблица 3).
4. Наивероятнейшее число успехов
Число k0 называется наивероятнейшим, если вероятность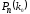 того, что событие A наступит в n испытаниях ровно k0 раз, является наибольшей из всех вероятностей
того, что событие A наступит в n испытаниях ровно k0 раз, является наибольшей из всех вероятностей 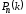 , k= 0, 1, … , n .
, k= 0, 1, … , n .
Наивероятнейшее число k0 определяется из двойного неравенства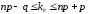 ,
,
причем:
а) если число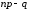 – нецелое, то существует единственное k0;
– нецелое, то существует единственное k0;
б) если число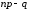 – целое, то наивероятнейших числа два, а именно:
– целое, то наивероятнейших числа два, а именно: 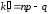 и
и 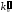 =
=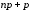 =
= 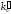 +1;
+1;
в) если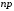 – целое, то
– целое, то 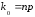 .
.
Пример 7. (Варианты 1, 7)
В семье пять детей. Найти вероятность того, что среди этих детей: а) ровно два мальчика; б) не более двух мальчиков
; в) более двух мальчиков; г) не менее двух и не более трех мальчиков. Вероятность рождения мальчика принять равной 0,51.
Решение:
Число испытаний n=5 невелико, поэтому вероятности можно вычислить непосредственно по формуле Бернулли.
а) Вероятность того, что среди пяти детей ровно два мальчика, равна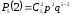 , где
, где 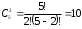 , p=0,51, q=1-p=0,49.
, p=0,51, q=1-p=0,49.
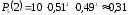 .
.
б) Вероятность того, что среди пяти детей не более двух мальчиков, равна
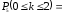
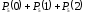 .
.
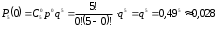 .
.
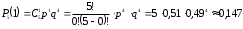
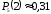 (см. а)).
(см. а)).
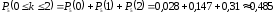
в) Событие {среди пяти детей более двух мальчиков} противоположно событию {среди пяти детей не более двух мальчиков}, поэтому его вероятность равна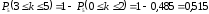 .
.
г) Вероятность того, что среди пяти детей не менее двух и не более трёх мальчиков, равна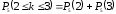 ,
, 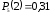 (см. а)).
(см. а)).
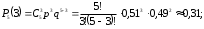
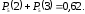
Пример 8. (Варианты 2, 9)
Сколько надо произвести независимых испытаний с вероятностью появления события в каждом испытании, равной 0,4, чтобы наивероятнейшее число появлений события в этих испытаниях было равно 25?
Решение:
По условию k0=25; р=0,4; q=0,6. Воспользуемся двойным неравенством np-q k0
k0 np+p. Подставляя данные задачи, получим систему неравенств для определения неизвестного числа n: 0,4n-0,6
np+p. Подставляя данные задачи, получим систему неравенств для определения неизвестного числа n: 0,4n-0,6  25, 0,4n+0,4
25, 0,4n+0,4 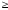 25. Из первого неравенства системы найдем
25. Из первого неравенства системы найдем
n 25,6/0,4=64. Из второго неравенства системы имеем n
25,6/0,4=64. Из второго неравенства системы имеем n 24,6/0,4=61,5. Итак, искомое число испытаний должно быть
24,6/0,4=61,5. Итак, искомое число испытаний должно быть 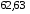 или 64.
или 64.
Пример 9. (Варианты 4, 6, 8, 10)
Вероятность появления события А в каждом из 2400 независимых испытаний постоянна и равна 0,6. Найти вероятность того, что событие А наступит: а) равно 1400 раз; б) от 1400 до 1800 раз; в) не менее 1400 раз.
Решение:
Число испытаний n=2400 велико; вероятность p=0,6 появления события A немала; q=1-p=0,4; npq=24000,60,4=14400,4 = 576 20, поэтому воспользуемся локальной и интегральной формулами Лапласа.
20, поэтому воспользуемся локальной и интегральной формулами Лапласа.
а) Имеем: n=2400, p=0,6, q=0,4, k=1400, np=1440, npq=576,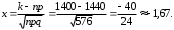 Функция
Функция  четная, поэтому
четная, поэтому 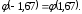 По таблице 1 приложения
По таблице 1 приложения 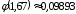 . По локальной приближенной формуле Лапласа
. По локальной приближенной формуле Лапласа 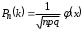 получим
получим 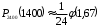

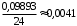 .
.
б) Имеем: n=2400, p=0,6, q=0,4, k1=1400, k2 =1800, np=1440,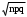 =24,
=24, 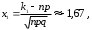
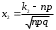
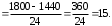 Функция
Функция  нечетная, поэтому
нечетная, поэтому 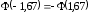 . По таблице 2 приложения находим
. По таблице 2 приложения находим 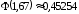 ,
, 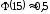 (т. к. при х5 полагают
(т. к. при х5 полагают  ).
).
По интегральной приближенной формуле Лапласа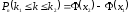
имеем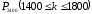

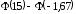
=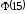
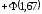
 0,5+0,45254= 0,95254.
0,5+0,45254= 0,95254.
в) Требование, чтобы событие появлялось не менее 1400 раз, означает, что максимально допустимое число появлений события A равно числу испытаний, т.е. k2=2400. В остальном решение задачи аналогично пункту б).
Пример 10. (Варианты 3, 5)
Тираж книги 100 000 экземпляров. Вероятность того, что она сброшюрована неправильно, равна 0,00001. Найти вероятность того, что тираж содержит ровно пять бракованных книг.
Решение:
События, состоящие в том, что книги бракованные, независимы. По условию число испытаний n=100 000 весьма велико, а вероятность р=0,00001 очень мала,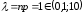 . Следовательно, можно использовать приближенную формулу Пуассона
. Следовательно, можно использовать приближенную формулу Пуассона 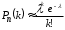 . По таблице 3 приложения для известных =1 и k=5 находим
. По таблице 3 приложения для известных =1 и k=5 находим 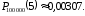
Приложение
Таблица 1. Значения локальной функции Лапласа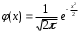 .
.
– вероятность того, что в п испытаниях событие A наступит не более m раз
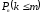 =
=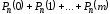 .
.– вероятность того, что в п испытаниях событие A наступит не менее
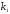 и не более
и не более 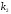 раз
раз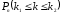 =
=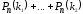 .
.Все эти вероятности могут быть вычислены по формуле Бернулли, однако, на практике ввиду вычислительных сложностей это возможно лишь при небольших n и поэтому используются приближенные формулы.
-
Приближенные формулы Муавра- Лапласа
2.1. Локальная теорема Лапласа
Если число испытаний n велико, а вероятность p не очень мала, то
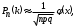
где
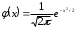 ,
, 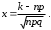
Значения функции
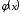 приведены в приложении (таблица 1), при
приведены в приложении (таблица 1), при 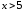 полагают
полагают 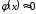 , для отрицательных значений x пользуются тем, что функция
, для отрицательных значений x пользуются тем, что функция 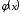 четная, и, следовательно,
четная, и, следовательно, 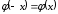 .
.2.2. Интегральная теорема Лапласа
Вероятность того, что событие А появится в n испытаниях не менее
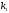 и не более
и не более 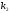 раз находится по формуле
раз находится по формуле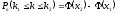 ,
,где
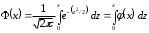 ,
, 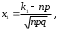
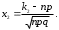
Значения функции Лапласа
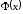
приведены в приложении (таблица 2), при
 полагают
полагают 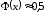 , для отрицательных значений x пользуются тем, что функция
, для отрицательных значений x пользуются тем, что функция  нечетная, и, следовательно,
нечетная, и, следовательно, 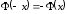 .
. -
Приближенная формула Пуассона
Если число испытаний n велико, а вероятность p появления события в каждом испытании очень мала, то
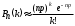 .
.Обозначив , =np– среднее число успехов в серии испытаний, получим
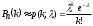 .
.Значение
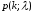 по заданным k и можно определить по приложению (таблица 3).
по заданным k и можно определить по приложению (таблица 3).4. Наивероятнейшее число успехов
Число k0 называется наивероятнейшим, если вероятность
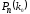 того, что событие A наступит в n испытаниях ровно k0 раз, является наибольшей из всех вероятностей
того, что событие A наступит в n испытаниях ровно k0 раз, является наибольшей из всех вероятностей 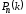 , k= 0, 1, … , n .
, k= 0, 1, … , n . Наивероятнейшее число k0 определяется из двойного неравенства
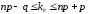 ,
,причем:
а) если число
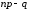 – нецелое, то существует единственное k0;
– нецелое, то существует единственное k0;б) если число
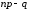 – целое, то наивероятнейших числа два, а именно:
– целое, то наивероятнейших числа два, а именно: 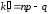 и
и 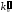 =
=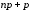 =
= 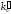 +1;
+1;в) если
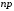 – целое, то
– целое, то 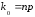 .
.Пример 7. (Варианты 1, 7)
В семье пять детей. Найти вероятность того, что среди этих детей: а) ровно два мальчика; б) не более двух мальчиков
; в) более двух мальчиков; г) не менее двух и не более трех мальчиков. Вероятность рождения мальчика принять равной 0,51.
Решение:
Число испытаний n=5 невелико, поэтому вероятности можно вычислить непосредственно по формуле Бернулли.
а) Вероятность того, что среди пяти детей ровно два мальчика, равна
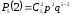 , где
, где 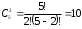 , p=0,51, q=1-p=0,49.
, p=0,51, q=1-p=0,49.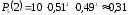 .
.б) Вероятность того, что среди пяти детей не более двух мальчиков, равна
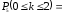
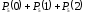 .
.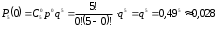 .
.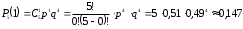
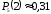 (см. а)).
(см. а)).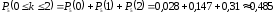
в) Событие {среди пяти детей более двух мальчиков} противоположно событию {среди пяти детей не более двух мальчиков}, поэтому его вероятность равна
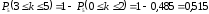 .
.г) Вероятность того, что среди пяти детей не менее двух и не более трёх мальчиков, равна
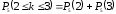 ,
, 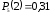 (см. а)).
(см. а)).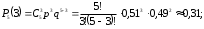
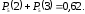
Пример 8. (Варианты 2, 9)
Сколько надо произвести независимых испытаний с вероятностью появления события в каждом испытании, равной 0,4, чтобы наивероятнейшее число появлений события в этих испытаниях было равно 25?
Решение:
По условию k0=25; р=0,4; q=0,6. Воспользуемся двойным неравенством np-q
 k0
k0 np+p. Подставляя данные задачи, получим систему неравенств для определения неизвестного числа n: 0,4n-0,6
np+p. Подставляя данные задачи, получим систему неравенств для определения неизвестного числа n: 0,4n-0,6  25, 0,4n+0,4
25, 0,4n+0,4 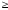 25. Из первого неравенства системы найдем
25. Из первого неравенства системы найдем
n
 25,6/0,4=64. Из второго неравенства системы имеем n
25,6/0,4=64. Из второго неравенства системы имеем n 24,6/0,4=61,5. Итак, искомое число испытаний должно быть
24,6/0,4=61,5. Итак, искомое число испытаний должно быть  или 64.
или 64.Пример 9. (Варианты 4, 6, 8, 10)
Вероятность появления события А в каждом из 2400 независимых испытаний постоянна и равна 0,6. Найти вероятность того, что событие А наступит: а) равно 1400 раз; б) от 1400 до 1800 раз; в) не менее 1400 раз.
Решение:
Число испытаний n=2400 велико; вероятность p=0,6 появления события A немала; q=1-p=0,4; npq=24000,60,4=14400,4 = 576
 20, поэтому воспользуемся локальной и интегральной формулами Лапласа.
20, поэтому воспользуемся локальной и интегральной формулами Лапласа.а) Имеем: n=2400, p=0,6, q=0,4, k=1400, np=1440, npq=576,
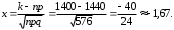 Функция
Функция  четная, поэтому
четная, поэтому 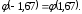 По таблице 1 приложения
По таблице 1 приложения 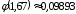 . По локальной приближенной формуле Лапласа
. По локальной приближенной формуле Лапласа 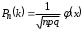 получим
получим 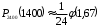

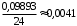 .
.б) Имеем: n=2400, p=0,6, q=0,4, k1=1400, k2 =1800, np=1440,
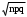 =24,
=24, 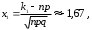
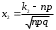
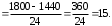 Функция
Функция  нечетная, поэтому
нечетная, поэтому 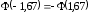 . По таблице 2 приложения находим
. По таблице 2 приложения находим 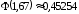 ,
, 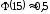 (т. к. при х5 полагают
(т. к. при х5 полагают  ).
).По интегральной приближенной формуле Лапласа
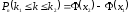
имеем
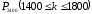

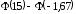
=
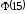
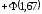
 0,5+0,45254= 0,95254.
0,5+0,45254= 0,95254.в) Требование, чтобы событие появлялось не менее 1400 раз, означает, что максимально допустимое число появлений события A равно числу испытаний, т.е. k2=2400. В остальном решение задачи аналогично пункту б).
Пример 10. (Варианты 3, 5)
Тираж книги 100 000 экземпляров. Вероятность того, что она сброшюрована неправильно, равна 0,00001. Найти вероятность того, что тираж содержит ровно пять бракованных книг.
Решение:
События, состоящие в том, что книги бракованные, независимы. По условию число испытаний n=100 000 весьма велико, а вероятность р=0,00001 очень мала,
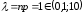 . Следовательно, можно использовать приближенную формулу Пуассона
. Следовательно, можно использовать приближенную формулу Пуассона 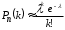 . По таблице 3 приложения для известных =1 и k=5 находим
. По таблице 3 приложения для известных =1 и k=5 находим 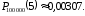
Приложение
Таблица 1. Значения локальной функции Лапласа
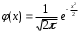 .
.| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0,0 | 0,3989 | 3989 | 3989 | 3988 | 39986 | 3984 | 3982 | 3980 | 3977 | 3973 |
| 0,1 | 0,3970 | 3965 | 3961 | 3956 | 3951 | 3945 | 3939 | 3932 | 3925 | 3918 |
| 0,2 | 0,3910 | 3902 | 3894 | 3885 | 3876 | 3867 | 3857 | 3847 | 3836 | 3825 |
| 0,3 | 0,3814 | 3802 | 3790 | 3778 | 3765 | 3752 | 3739 | 3726 | 3712 | 3697 |
| 0,4 | 0,3683 | 3668 | 3653 | 3637 | 3621 | 3605 | 3589 | 3572 | 3555 | 3538 |
| 0,5 | 0,3521 | 3503 | 3485 | 3467 | 3448 | 3429 | 3410 | 3391 | 3372 | 3352 |
| 0,6 | 0,3332 | 3312 | 3292 | 3271 | 3251 | 3230 | 3209 | 3187 | 3166 | 3144 |
| 0,7 | 0,3123 | 3101 | 3079 | 3056 | 3034 | 3011 | 2989 | 2966 | 2943 | 2920 |
| 0,8 | 0,2897 | 2874 | 2850 | 2827 | 2803 | 2780 | 2756 | 2732 | 2709 | 2685 |
| 0,9 | 0,2661 | 2637 | 2613 | 2589 | 2565 | 2541 | 2516 | 2492 | 2468 | 2444 |
| | | | | | | | | | | |
| 1,0 | 0,2420 | 2396 | 2371 | 2347 | 2323 | 2299 | 2275 | 2251 | 2227 | 2203 |
| 1,1 | 0,2179 | 2155 | 2131 | 2107 | 2083 | 2059 | 2036 | 2012 | 1989 | 1965 |
| 1,2 | 0,1942 | 1919 | 1895 | 1872 | 1849 | 1826 | 1804 | 1781 | 1758 | 1736 |
| 1,3 | 0,1714 | 1691 | 1669 | 1647 | 1626 | 1604 | 1582 | 1561 | 1539 | 1518 |
| 1,4 | 0,1497 | 1476 | 1456 | 1435 | 1415 | 1394 | 1374 | 1354 | 1334 | 1315 |
| 1,5 | 0,1295 | 1276 | 1257 | 1238 | 1219 | 1200 | 1182 | 1163 | 1145 | 1127 |
| 1,6 | 0,1109 | 1092 | 1074 | 1057 | 1040 | 1023 | 1006 | 0989 | 0973 | 0957 |
| 1,7 | 0,0940 | 0925 | 0909 | 0893 | 0878 | 0863 | 0848 | 0833 | 0818 | 0804 |
| 1,8 | 0,0790 | 0775 | 0761 | 0748 | 0734 | 0721 | 0707 | 0694 | 0681 | 0669 |
| 1,9 | 0,0656 | 0644 | 0632 | 0620 | 0608 | 0596 | 0584 | 0573 | 0562 | 0551 |
| | | | | | | | | | | |
| 2,0 | 0,0540 | 0529 | 0519 | 0508 | 0498 | 0488 | 0478 | 0468 | 0459 | 0449 |
| 2,1 | 0,0440 | 0431 | 0422 | 0413 | 0404 | 0396 | 0387 | 0379 | 0371 | 0363 |
| 2,2 | 0,0355 | 0347 | 0339 | 0332 | 0325 | 0317 | 0310 | 0303 | 0297 | 0290 |
| 2,3 | 0,0283 | 0277 | 0270 | 0264 | 0258 | 0252 | 0246 | 0241 | 0235 | 0229 |
| 2,4 | 0,0224 | 0219 | 0213 | 0208 | 0203 | 0198 | 0194 | 0189 | 0184 | 0180 |
| 2,5 | 0,0175 | 0171 | 0167 | 0163 | 0158 | 0154 | 0151 | 0147 | 0143 | 0139 |
| 2,6 | 0,0136 | 0132 | 0129 | 0126 | 0122 | 0119 | 0116 | 0113 | 0110 | 0107 |
| 2,7 | 0,0104 | 0101 | 0099 | 0096 | 0093 | 0091 | 0088 | 0086 | 0084 | 0081 |
| 2,8 | 0,0079 | 0077 | 0075 | 0073 | 0071 | 0069 | 0067 | 0065 | 0063 | 0061 |
| 2,9 | 0,0060 | 0058 | 0056 | 0055 | 0053 | 0051 | 0050 | 0048 | 0047 | 0046 |
| | | | | | | | | | | |
| 3,0 | 0,0044 | 0043 | 0042 | 0040 | 0039 | 0038 | 0037 | 0036 | 0035 | 0034 |
| 3,1 | 0,0033 | 0032 | 0031 | 0030 | 0029 | 0028 | 0027 | 0026 | 0025 | 0025 |
| 3,2 | 0,0024 | 0023 | 0022 | 0022 | 0021 | 0020 | 0020 | 0019 | 0018 | 0018 |
| 3,3 | 0,0017 | 0017 | 0016 | 0016 | 0015 | 0015 | 0014 | 0014 | 0013 | 0013 |
| 3,4 | 0,0012 | 0012 | 0012 | 0011 | 0011 | 0010 | 0010 | 0010 | 0009 | 0009 |
| 3,5 | 0,0009 | 0008 | 0008 | 0008 | 0008 | 0007 | 0007 | 0007 | 0007 | 0006 |
| 3,6 | 0,0006 | 0006 | 0006 | 0005 | 0005 | 0005 | 0005 | 0005 | 0005 | 0004 |
| 3,7 | 0,0004 | 0004 | 0004 | 0004 | 0004 | 0004 | 0003 | 0003 | 0003 | 0003 |
| 3,8 | 0,0003 | 0003 | 0003 | 0003 | 0003 | 0002 | 0002 | 0002 | 0002 | 0002 |
| 3,9 | 0,0002 | 0002 | 0002 | 0002 | 0002 | 0002 | 0002 | 0002 | 0001 | 0001 |
| 4,0 | 0,0001338 | | 0000589 | | 0000249 | | 0000101 | | 0000040 | |
| 5,0 | 0,0000015 | | | | | | | | | |