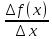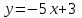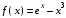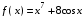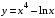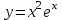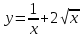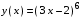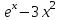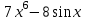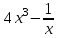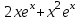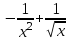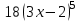Файл: Камбулатова Люция Дамировна Место работы мбоу сош 11, г. Алексин, Тульская область общая информация по уроку класс укажите класс, к которому относится урок.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 29
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практическая работа: разработка технологической карты урока
Инструкция по выполнению практической работы: выберите класс, тему урока в соответствии с ПРП и заполните представленную ниже таблицу. Для каждого учебного задания, включенного в урок, укажите планируемые результаты, на достижение которых это задание направлено.
1. ИНФОРМАЦИЯ О РАЗРАБОТЧИКЕ ПЛАНА
| ФИО разработчика | Камбулатова Люция Дамировна |
| Место работы | МБОУ СОШ № 11, г . Алексин, Тульская область |
2. ОБЩАЯ ИНФОРМАЦИЯ ПО УРОКУ
| Класс (укажите класс, к которому относится урок): | 11 |
| Место урока (по тематическому планированию ПРП) | Производная и её геометрический смысл. (II четверть) |
| Тема урока | Определение производной функции, её геометрический смысл |
| Уровень изучения (укажите один или оба уровня изучения (базовый, углубленный), на которые рассчитан урок): | Базовый |
| Тип урока (укажите тип урока): | ☐ урок освоения новых знаний и умений ☐ урок-закрепление ☐ урок-повторение ☐ урок систематизации знаний и умений ☐ урок развивающего контроля ☐ комбинированный урок ☐ другой (впишите) |
| Планируемые результаты (по ПРП): | |
| Личностные: формировать устойчивый познавательный интерес, необходимость приобретения новых знаний, умение ясно, точно, грамотно излагать свои мысли | |
| Метапредметные
| |
| Предметные:
| |
| Ключевые слова (введите через запятую список ключевых слов, характеризующих урок): производная функции в точке, геометрический смысл | |
| Краткое описание (введите аннотацию к уроку, укажите используемые материалы/оборудование/электронные образовательные ресурсы) Применение производной в физике, химии, экономике. Алгебра и начала математического анализа. 11 класс: учебник для общеобразовательных. учреждений: базовый и профильный уровни / Ю. М. Колягин, М. В. Ткачева, Н. Е. Федорова, М.И. Шабунин/ М.: Просвещение 2011» http://pedsovet.su/load/135 http://www.uchportal.ru/load/28 http://mathege.ru:8080/or/ege/ Доска, компьютер, проектор, экран, две самостоятельные работы; карточки с заданиями для учащихся, работающих в группах, тексты дифференцированной самостоятельной работы, карточки с таблицей для рефлексии. | |
3. БЛОЧНО-МОДУЛЬНОЕ ОПИСАНИЕ УРОКА
| БЛОК 1. Вхождение в тему урока и создание условий для осознанного восприятия нового материала | ||||
| Этап 1.1. Мотивирование на учебную деятельность | ||||
| Укажите формы организации учебной деятельности на данном этапе урока. Опишите конкретную учебную установку, вопрос, задание, интересный факт, которые мотивируют мыслительную деятельность школьника (это интересно/знаешь ли ты, что) | ||||
| Приветствие, проверка готовности к уроку, организация внимания (2 минуты) Создать благоприятный психологический настрой на работу. Сегодня на уроке мы вспомним понятие тангенса прямоугольного треугольника, рассмотрим скорость изменения функции. Рассмотрим новую тему: «Определение производной и её геометрический смысл» | ||||
| Этап 1.2. Актуализация опорных знаний | ||||
| Укажите формы организации учебной деятельности и учебные задания для актуализации опорных знаний, необходимых для изучения нового | ||||
| Повторение материала прошлого урока. Организует фронтальную беседу о теме, целях и плане урока. Показывает слайды с темой и целями урока. Фронтальная беседа с классом. На предыдущих уроках мы ввели понятия «приращение аргумента» и «приращение функции», научились находить отношение приращения функции к приращению аргумента, а также предел этого отношения при условии, что Δx 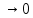 . . Эти понятия позволят нам рассмотреть задачи, которые приведут нас к очень важному в математике понятию – понятию «производной».
Чему равны tgA, tgB?
Учитель направляет и поправляет. | ||||
| Этап 1.3. Целеполагание | ||||
| Назовите цель (стратегия успеха): ты узнаешь, ты научишься | ||||
| Обеспечение мотивации учения, формулировка целей урока. Вспомним, что мы делали на предыдущем уроке? Мы ввели понятия «приращение аргумента» и «приращение функции», находили отношение приращения функции к приращению аргумента, а также предел этого отношения при условии, что Δx 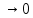 . . Вернемся к выполненной работе и теме урока. Что будем делать на уроке? Проговаривает тему урока, цели урока. Всё это позволит нам рассмотреть задачи, которые приведут к очень важному в математике понятию – понятию «производной». | ||||
| БЛОК 2. Освоение нового материала | ||||
| Этап 2.1. Осуществление учебных действий по освоению нового материала | ||||
| Укажите формы организации учебной деятельности, включая самостоятельную учебную деятельность учащихся (изучаем новое/открываем новое). Приведите учебные задания для самостоятельной работы с учебником, электронными образовательными материалам (рекомендуется обратить внимание учеников на необходимость двукратного прочтения, просмотра, прослушивания материала. 1) на общее понимание и мотивацию 2) на детали). Приведите задания по составлению плана, тезисов, резюме, аннотации, презентаций; по наблюдению за процессами, их объяснением, проведению эксперимента и интерпретации результатов, по построению гипотезы на основе анализа имеющихся данных и т. д. | ||||
| Обеспечение восприятия, осмысления и первичного запоминания изучаемой темы: «Определение производной функции, её геометрический смысл» Предупреждает, что учащиеся должны в тетради делать краткие записи за учителем и со слайдов, на которых пометка «Конспект» . Рассмотрим две задачи, приводящие к понятию производной: о скорости изменения функции и о скорости движения Задача 1. На слайде представлен график некоторой функции и касательная в точке. Оценим на сколько круто идет график вверх? Угол наклона-это угол между касательной и положительным направлением оси ОХ
Производная и есть тангенс угла наклона касательной в данной точке. А что такое производная? Какого её определение в математике? Задача 2. Рассмотрим прямолинейное движение некоторого тела.
Закон движения задан формулой S = S(t), т.е. каждому моменту времени t соответствует определённое значение пройденного пути S. Найти скорость движения тела в момент времени t. Решение:  Пусть в момент времени t тело находится в точке М. Дадим аргументу t приращение Δt, за это время тело переместится в некоторую точку Р, т. е. пройдёт путь ΔS. Итак, за время Δt тело прошло путь ΔS. Что можно найти, зная эти два значения? 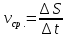 , т. е. среднюю скорость движения тела за промежуток времени , т. е. среднюю скорость движения тела за промежуток времени 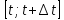 . .Определение:Средней скоростью движения тела называется отношение пройденного пути ко времени, в течение которого этот путь пройден.
Можно рассуждать так: мгновенную скорость получим если Δt  , т. е. Δt выбирается всё меньше и меньше, т. е. , т. е. Δt выбирается всё меньше и меньше, т. е. 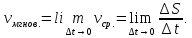 Можно указать ещё много задач из физики, геометрии, для решения которых необходимо отыскать скорость изменения соответствующей функции. Например, отыскание угловой скорости вращающегося тела, отыскание теплоёмкости тела при нагревании, линейный коэффициент расширения тел при нагревании, скорость химической реакции в данный момент времени и т. п. Все эти задачи требуют для своего решения нахождения скорости изменения соответствующей функции. Ввиду обилия задач, приводящих к вычислению скорости изменения функции или, иначе, к вычислению предела отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, оказалось необходимым выделить такой предел для произвольной функции и изучить его основные свойства. Этот предел называется производной функции. А что такое производная?
Обозначение производной: 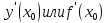 . Тогда . Тогда 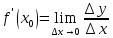 или или 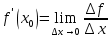 Проанализируем определение производной и составим алгоритм её нахождения.
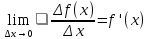 С помощью этого алгоритма можно найти производную любой функции, т. е. получить таблицу производных, а также доказать правила вычисления производных, которыми в дальнейшем мы и будем пользоваться. Например, найти производную функции f(x) = x2 +1 в точке x0 = -2.
Ведет беседу, направляя и подсказывая. Записывает необходимое на доске. Выдаёт сформулированный алгоритм нахождения производной функции | ||||
| Этап 2.2. Проверка первичного усвоения | ||||
| Укажите виды учебной деятельности, используйте соответствующие методические приемы. (Сформулируйте/Изложите факты/Проверьте себя/Дайте определение понятию/Установите, что (где, когда)/Сформулируйте главное (тезис, мысль, правило, закон) | ||||
| Формирование навыка нахождения производной некоторых функций, используя алгоритм нахождения производной; составление таблицы производных; выявление недостатков в знаниях и способах действий, установление причин выявленных недостатков. Первый пример учитель рассматривает совместно с учащимися с оформлением решения на доске и образцом записи в тетради. Все следующие примеры решаются учащимися в парах (учитель – консультант), с последующей проверкой на мультимедийной презентации Организует работу в парах, консультирует.
Найти производную функции y = C. Решение: f 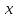 ) = C ) = C1.Возьмём два значения аргумента 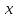 и и 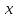 + Δ + Δ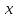 . .2. 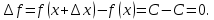 3. 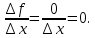 4. 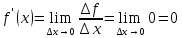 . .Значит, 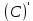 = 0 или производная постоянной равна нулю. = 0 или производная постоянной равна нулю.Работа в парах:
Найти производную функции y = x Решение: f( 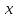 ) = ) =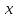 . .1.Возьмём два значения аргумент 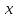 и и 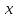 + Δ + Δ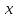 . .2. 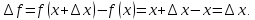 3. 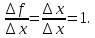 4. 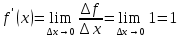 . .Значит, 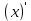 = 1. = 1.
Найти производную функции y = x2 Решение: f( 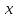 ) = ) = 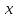 2. 2.1.Возьмём два значения аргумента 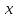 и и 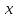 + Δ + Δ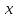 . .2. 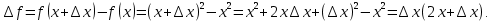 3. 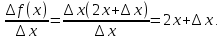 4. 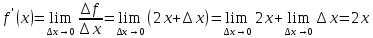 . .Значит, 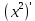 = 2x. = 2x.
Найти производную функции y = 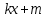 Решение: f(x) = 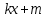 . .1.Возьмём два значения аргумента 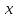 и и 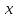 + Δ + Δ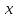 . .2. 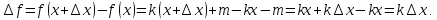 3. 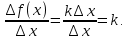 4. 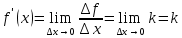 . .Значит, 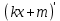 = k. = k.
Найти производную функции y = 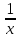 Решение: f(x) = 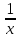 . .1.Возьмём два значения аргумента 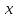 и и 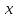 + Δ + Δ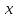 . .2. 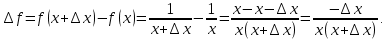 3. 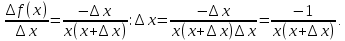 4. 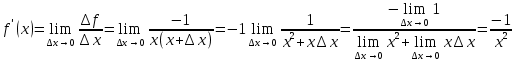 . .Значит, 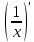 = = 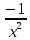 . .Итак, с помощью определения производной, можно найти производную любой функции. Запишем найденные производные в таблицу и в дальнейшем будем ей пользоваться. Таблица производных 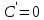 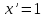 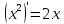 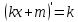 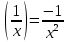 Выдаёт таблицы каждому | ||||
| БЛОК 3. Применение изученного материала | ||||
| Этап 3.1. Применение знаний, в том числе в новых ситуациях | ||||
| Укажите формы организации соответствующего этапа урока. Предложите виды деятельности (решение задач, выполнение заданий, выполнение лабораторных работ, выполнение работ практикума, проведение исследовательского эксперимента, моделирование и конструирование и пр.), используйте соответствующие методические приемы (используй правило/закон/формулу/теорию/идею/принцип и т.д.; докажите истинность/ложность утверждения и т.д.; аргументируйте собственное мнение; выполните задание; решите задачу; выполните/сделайте практическую/лабораторную работу и т.д.). | ||||
| Блиц-опрос «Верно-неверно» Если ученик согласен с ответом – он ставит у себя в тетради «+», если – нет «-«. Цель данного задания – понимание смысла теоретических знаний.
Ответы: + - + + - + + Откройте учебник на с. 96. Запишите номера, которые мы будем выполнять, по желанию у доски или самостоятельно в тетради на оценку. №224(1-3), №225(1-2), №227(5-7). | ||||
| Этап 3.2. Выполнение межпредметных заданий и заданий из реальной жизни | ||||
| Подберите соответствующие учебные задания | ||||
| Задача. Материальная точка движется прямолинейно по закону х(t)=-1/4 ????^2+8t+14, где х –расстояние от точки отсчета в м, t- время в секундах, измеренное с начала движения. Найдите ее скорость (м/с) в момент времени t=8с | ||||
| Этап 3.3. Выполнение заданий в формате ГИА (ОГЭ, ЕГЭ) | ||||
| Подберите соответствующие учебные задания | ||||
| ИЗ ОТКРЫТОГО БАНКА ЗАДАНИЙ 1в
 В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней. ТОЧКИ ЗНАЧЕНИЯ ПРОИЗВОДНОЙ A 1) 0,5 B 2) − 0,7 C 3) 4 D 4) −3 В таблице под каждой буквой укажите соответствующий номер.
 В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней. ТОЧКИ ЗНАЧЕНИЯ ПРОИЗВОДНОЙ A 1) − 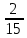 B 2) 2 C 3) 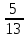 D 4) − 1 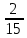 В таблице под каждой буквой укажите соответствующий номер.
в точке x0. 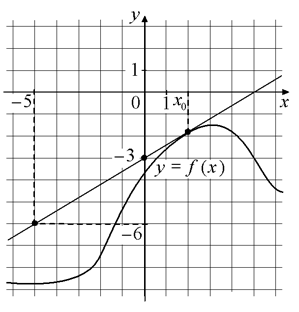
в точке x0. 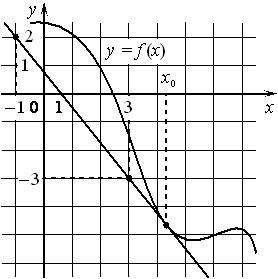 | ||||
| Этап 3.4. Развитие функциональной грамотности | ||||
| Подберите соответствующие учебные задания | ||||
| Задачи по формированию функциональной грамотности, в частности, математической грамотности обучающихся, возможно реализовать при условии оптимального сочетания учебного содержания базового уровня образования и дополнительных курсов, направленных на совершенствование прикладных математических умений, использующихся в различных жизненных ситуациях. Задание 1. На рисунках изображены графики функций и касательные, проведенные к ним в точках с абсциссами х0. Установите соответствие между графиками функций и значениями производной этих в точках х0. Значения производных:
В ответе запишите четырехзначное число. 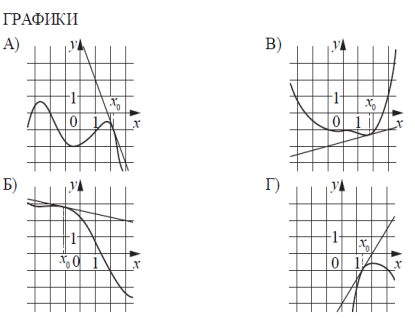 | ||||
| Этап 3.5. Систематизация знаний и умений | ||||
| Подберите учебные задания на выявление связи изученной на уроке темы с освоенным ранее материалом/другими предметами | ||||
| закрепление изученных способов решения и применение знаний в новых ситуациях. Итак, ребята, сейчас вы должны применить сведения, которые повторили на уроке, на практике.
| ||||
| БЛОК 4. Проверка приобретенных знаний, умений и навыков | ||||
| Этап 4.1. Диагностика/самодиагностика | ||||
| Укажите формы организации и поддержки самостоятельной учебной деятельности ученика, критерии оценивания | ||||
| индивидуальная рефлексия достижения цели и создание (по возможности) ситуации успеха; закрепление знания способов решения Итак, наш урок близится к концу. В своих рабочих тетрадях выполните задания на карточках: Вариант 1 Найти производную функции f(x) = х + 3 в точке  = 4 = 4Вариант 2 Найти производную функции f(x) = 2х + 1 в точке  = 1 = 1Вариант 3 Найти производную функции f(x) = 4х + 2 в точке 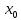 = -1 = -1Вариант 4 Найти производную функции f(x) = х2 - 1 в точке 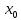 = 1 = 1Вариант 5 Найти производную функции f(x) = х2 + 3 в точке 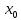 = -1 = -1 | ||||
| БЛОК 5. Подведение итогов, домашнее задание | ||||
| Этап 5.1. Рефлексия | ||||
| Введите рекомендации для учителя по организации в классе рефлексии по достигнутым либо недостигнутым образовательным результатам | ||||
| Организовать рефлексию учащихся по их собственной деятельности и взаимодействия с учителем и другими учениками в классе Проанализируйте результаты своей деятельности в соответствии с поставленной целью урока. Закончи фразу:
| ||||
| Этап 5.2. Домашнее задание | ||||
| Введите рекомендации по домашнему заданию. | ||||
| Обеспечить осознания учащимися своей учебной деятельности на уроке. Дать качественную оценку работы класса и отдельных учащихся Поставьте себе оценку за урок на полях тетради, итоговую оценку вы получите после проверки выполнения заданий на карточках Подводит итог урока. Домашнее задание: Базовый уровень: № 243(2) Высокий уровень: № 244(3), № 245 Повышенный уровень: № 249, № 250(1) По желанию можно выполнить дома задания из самостоятельной работы творческого уровня (на карточках). |