ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 19
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1.Жиындардың берілу тәсілдері.
Жиын ұғымы математиканың негізгі, алғашқы ұғымдарының бірі, сондықтан ол басқа ұғымдар арқылы анықталмайды. Жиындар теориясының негізін қалаған неміс математигі Георг Кантор (1845-1918) жиын түсінігін келесі түрде анықтаған: «Бірнеше заттардың, объектілердің қандай да бір белгісіне қарай біртұтас болып бірігуі жиынды анықтайды». Сан ұғымынан бұрын шыққан жиын ұғымын қандай да бір нәрселердің жинағы ретінде түсінеміз, ол жинаққа кіретін нәрселерді жеке-жеке қабылдауға және оларды бір-бірінен де, бұл жинаққа жатпайтын басқа нәрселерден де ажыратуға болады деп білеміз. Яғни, жиын туралы сөз еткенде, қандай да бір белгілері бойынша бір тұтас етіп біріктірілген нәрселерді қарастырамыз.
Мүшелерін тізіп жазу және сипаттау арқылы.Мүшелерін тізіп жазу арқылы. Бұл тәсілмен тек қана ақырлы жиындарберіледі. Мысалы, процессор a, монитор b, клавиатура c және принтерден d тұратын компьютер А жиынын былай өрнектеуге болады: A = {a, b, c, d}, ақырлы жиын
.Ақырсыз жиындарды тізіммен беру мүмкін емес. Мысалы, барлық натурал сандардың немесе барлық бүтін сандардың жиынын тізім арқылы беру, яғни ол жиындардың барлық элементтерінің тізімін жасау мүмкін емес.
-
Ең болмағанда А жиынына немесе В жиынына тиісті элементтер жиынын А және В жиындарының бірігуі (қосындысы)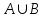
деп атаймыз. -
А жиынына да В жиынына да тиісті элементтер жиынын А және В элементтер жиынының қиылысуы (көбейтіндісі) деп аталады.
7.Группалар,сақиналар,өріс