Добавлен: 03.12.2023
Просмотров: 23
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
 |
| МИНОБРНАУКИ РОССИИ |
| Федеральное государственное бюджетное образовательное учреждение высшего образования «МИРЭА - Российский технологический университет» РТУ МИРЭА |

Филиал РТУ МИРЭА в г. Фрязино Кафедра общенаучных дисциплин
ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №8
по дисциплине
«Физика»
ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ ПАДЕНИЯ С ПОМОЩЬЮ ФИЗИЧЕСКОГО МАЯТНИКА
Выполнил студент группы ФВБО-01-22 Кукин Н.А.
(учебная группа)
 Принял
Принялдоценткафедры ОНДБелихов А.Б.
Лабораторные работы выполнены «13» сентября 2022 г.
«Зачтено»
«3» октября 2022 г.
Фрязино 2022
-
Теоретическое введение.
Физическим маятником называется тело, могущее совершать колебания около оси, смещенной относительно цента тяжести этого тела.
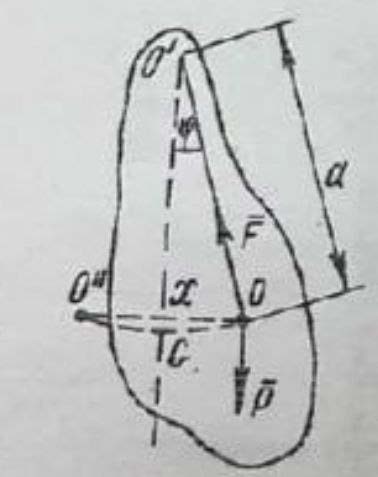 На рисунке изображён схематический физический маятник, колеблющийся в поле тяжести около горизонтальной оси О’ перпендикулярной плоскости чертежа.
На рисунке изображён схематический физический маятник, колеблющийся в поле тяжести около горизонтальной оси О’ перпендикулярной плоскости чертежа.Если углы отклонения не превышает 5-6о, то маятник совершает гармонические колебания. Докажем это. Обратим внимание на то, что центр тяжести О маятника перемещается по дуге О”СО окружности радиуса ОО’, другие его точки – по дугам окружностей соответствующих радиусов. Имеет место вращательное движение относительно
оси О’.
Внешнее воздействие на маятник определяется моментами сил F и P, причём векторы сил приложены к центру тяжести тела.
Результирующий момент этих сил равен: M = −Px. (1)
Плечо для сил F равно нулю, поскольку линия действия силы пересекает ось О’.
Плечо для силы Р обозначено х. Знак минус поставлен потому, что момент силы действует в направлении уменьшения х.
Вращающий момент М создаёт угловое ускорение ε. Запишем второй закон динамики для вращательного движения
M = Jε (2)
Здесь J – момент инерции физического маятника относительно оси вращения О’. Угловым ускорение определяется:
Объединим (3), (2) и (1). Получим:
ε = d2φ
 dl2
dl2(3)
????2???? ????

 ????????2 = − ???? ???? (4)
????????2 = − ???? ???? (4)При углах отклонения до 60 справедливы соотношения:
 sin ???? ≈ ????; ???? ≈ ????
sin ???? ≈ ????; ???? ≈ ????????
(5)
где а – расстояние от центра тяжести до оси вращения.
Дифференцируем (5) и подставляем в (4). Имеем:

 ????2???? = − ???????? ???? (6)
????2???? = − ???????? ???? (6)????????2 ????
Решением дифференцированного уравнения (6) является:
???? = ????0
sin


�
???????? ???? (7)
????
в чём можно убедится, если дифференцировать (7) дважды и поставить в (6).
Следовательно, при малых отклонениях физического маятника он совершает гармоническое (синусоидальное) колебания.
Определим период колебания физического маятника. Для этого напомним формулу смещения для синусоидальных колебаний:
x = x0
Сравнивая уравнения (8) с (7) получим:
sin 2π
 Tφ
Tφ(8)

Или
????
???????? = 2 �
1
 ????????
????????(9)

�
???????? = 2???? 1
????????????????
(10)
Уравнение (10) представляет собой формулу для периода колебания физического маятника. В нём m – масса физического маятника.
Математический маятник является частным случаем физического маятника, который представляет собой материальную точку, укрепленную на невесомой, нерастяжимой нити.
Момент инерции точки массы m относительно оси О’:
???? = ????????2 (11)


Вычислим период колебания математического маятника Тм. Для этого в (10) подставим (11). Имеем:
Т = 2????�????????2 ; ???? = 2????�???? .

м ???????????????? ????
????????
Сравнивая (12) с (10) даёт, если Тм = Тф:
????????????
= ????
 ????????
????????.(13)
Формула (13) определяет так так называемую приведенную длину физического маятника (lnp). Приведённой длинной физического маятника называется длина такого математического маятника, который имеет период колебания, равный с физическим.
-
Описание аппаратуры и метода измерений.
Физическим маятником млужит однородный металлический стержень. Он, опираясь с помощью муфты на призмы, может совершать колебания в плоскости, параллельной стене, относительно горизонтальной оси О’. Ось вращения совпадает с ребрами опорных призм.
Момент инерции J стержня (без учета муфты) относительно оси определим, исходя из теоремы Штейна:
J = J0 + ma2 (14)
где J0 – момент инерции стрежня относительно его центра тяжести: а – расстояние между осью вращения и центром тяжести, причем
где ????2 – длинна стержня.
????0
= 1 ????????2 (15)
 12
12Подставим (15) в (14), а (14) в (10). Получим, решая (10) относительно g:

3????????2
???? = ????2(????2+12????2)
ф
(16)
Измеряя период колебания физического маятника Тф, длину стержня L и удаление выреза муфты от центра стрежня a, можно вычислить по формуле (16) ускорение свободного падения g.
-
Обработка результатов измерения.
| | Опыт 1 | ||||
| a | n | t | T | ||
| № измерения | 1 | 38,75 | 18 | 28,68 | 1,59 |
| 2 | 18 | 28,43 | 1,53 | ||
| 3 | 18 | 28,90 | 1,60 | ||
| 4 | 18 | 28,73 | 1,59 | ||
| 5 | 18 | 28,94 | 1,60 | ||
| | Опыт 2 | ||||
| a | n | t | T | ||
| № измерения | 1 | 31,75 | 18 | 28,35 | 1,57 |
| 2 | 18 | 28,26 | 1,57 | ||
| 3 | 18 | 28,27 | 1,57 | ||
| 4 | 18 | 28,30 | 1,57 | ||
| 5 | 18 | 28,33 | 1,57 | ||
| | Опыт 3 | ||||
| a | n | t | T | ||
| № измерения | 1 | 24,75 | 18 | 27,90 | 1,95 |
| 2 | 18 | 27,85 | 1,54 | ||
| 3 | 18 | 28,10 | 1,56 | ||
| 4 | 18 | 28,11 | 1,56 | ||
| 5 | 18 | 27,99 | 1,55 | ||
| | g | ||
| Опыт 1 | Опыт 2 | Опыт 3 | |
| 1 | 9,8859 | 9,8879 | 10,3906 |
| 3 | 10,0115 | 9,8879 | 10,5262 |
| 3 | 9,7628 | 9,8879 | 10,2581 |
| 4 | 9,8859 | 9,8879 | 10,2581 |
| 5 | 9,7628 | 9,8879 | 10,3906 |
???? =
∆????
 =
=????
2∆????
 +
+????
2(????∆???? + 12????∆????)
 ????2 + 12????2 +
????2 + 12????2 +∆????
 +
+????
2∆????

????
 ∆???? = ∆????; ∆???? = ????????
∆???? = ∆????; ∆???? = ????????????
g = 9,76 ± 0,07
Задача из сборника Иродова 1.85
Небольшой шарик массы m, подвешенный на нити, отвели в сторону так, что нить образовала прямой угол с вертикалью, и затем отпустили. Найти:
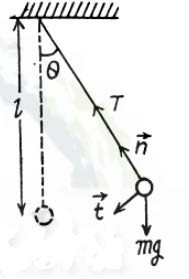 а) полное ускорение шарика и натяжение нити в зависимости от — угла отклонения нити от вертикали
а) полное ускорение шарика и натяжение нити в зависимости от — угла отклонения нити от вертикалиб) натяжение нити в момент, когда вертикальная составляющая скорости шарика максимальна
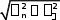 полн
полн gsin
 V2
V2
 an ???? ????
an ???? ????