Тәуелсiз қайталамалы тәжiрибелер

1. 
   Бернулли -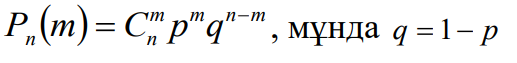
   
2. 
   Пуассон -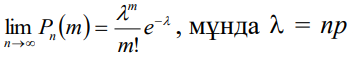
   
3. 
   Муавр-Лапластың локальдық теоремасы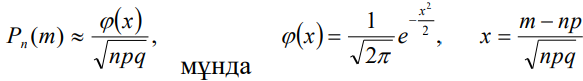
   
4. 
   Муавр-Лапластың интегралдық теоремасы
   

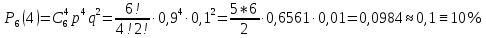
мұнда Мысал1. Автоматты станокпен стандарт тетіктер жасау ықтималдығы 0,9-ға тең. Кездейсоқ алынған 6 тетіктің 4-еуі стандарт болу ықтималдығын табу керек.Есептің шарты бойынша тәжірибе бірдей жағдайда қайталанады. Сондықтан ???? = 0,9; ???? = 0,1; ???? = 6, ???? = 4Мысал 2. Мысалы ???? = 50, m = 30, ???? = 0,2 болсын. Онда 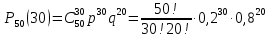(-) шешімдін мағнасы жоқБұл өрнекті есептеу өте күрделі. Бұларды жуықтап есептейміз. Сонда қателік жібереміз. Бұл қателік өсе беруі мүмкін, қорытындысында басқа нәтиже алуымыз мүмкін.Сынақ саны ???? мейлінше үлкен болып, ???? -ның мәні 0 мен 1 аса жуық болмасын.Мысал 3. ???? оқиғаның 400 сынақта дәл 80 рет пайда болу ықтималдығын табу керек, егер әрбір сынақта ???? –ның пайда болу ықтималдығы 0,2-ге тең болса. Шешуі: Шарт бойынша ???? = 400, ???? = 80, ???? = 0,2; ???? 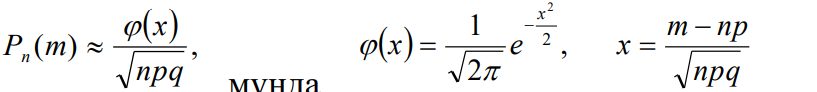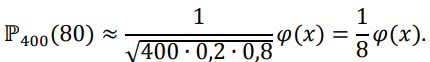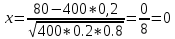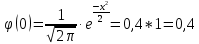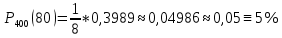= 0,8.Мысал 4. Жаңа мөлтек ауданда үйлердің кіретін есігіне коды бар 10000 құлып қойылған. Бір ай ішінде құлыптың істен шығу ықтималдығы: а) 0,0002; б) 0,001. Бір айда екі , үш және бес құлып істеп шығу ықтималдығын тап.Пуассон формуласын қолданамыз

---

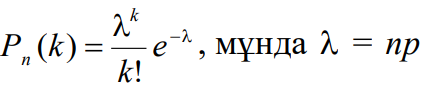
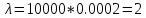
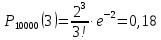
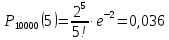
Мысал 5. Ұшып бара жатқан самолетті бір рет атқанда оқтың тию ықтималдығы ???? = 0,01-ге тең. Самолетті 100 рет атқанда екі оқтың тию ықтималдығын табу керек. Шешуі: Шарт бойынша ???? = 100, ???? = 0,01, ???? = 2, 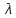= ???????? = 100 ∙ 0,01 = 1. Пуассон теоремасы бойынша

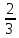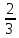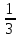
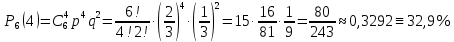
Пример 2. Стрелок делает 6 выстрелов по мишени. Вероятность попадания при одном выстреле . Найти вероятность того, что он попал 4 разаn=6, m=4, p= , q=Пример 3. В результате обследования были выделены семьи, имеющие по 4 ребенка. Считая вероятности появления мальчика и девочки в семье равными, определить вероятности появления в ней: а) одного мальчика; б) двух мальчиков.Решение:а) n=4; m=1; p=0,5; q=0,5 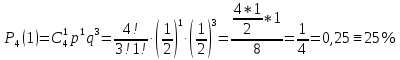- вероятность того, что среди 4 детей будет один мальчикб) n=4; m=2; p=0,5; q=0,5 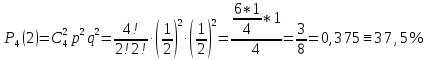- вероятность того, что среди 4 детей будет два мальчика.Пример 4.Статистика аудиторских проверок компании утверждает, что вероятность обнаружения ошибки в каждом проверяемом документе равна 0,1. Какова вероятность, что из десяти проверяемых документов девять из них не будет содержать ошибки? Пример 5.По данным технического контроля 2% изготовленных станков нуждаются в дополнительной регулировке. Найти вероятность того, что из 6 изготовленных станков 4 нуждаются в дополнительной регулировке.Пример 6.Производится 5 выстрелов в мишень. Вероятность попадания при каждом выстреле равна 3/4 . Найти вероятность того, что в мишени будет не менее трѐх, но и не более четырѐх пробоин. Найти наивероятнейшее число попаданий и соответствующую ему вероятность.

---

Смотрите также файлы

• Задача Заполнить расходные и приходные кассовые ордера, лист кассовой книги по следующим фактам хозяйственной жизни.docx

• Начало Эпохи эвм.odt

• Задача Проверка кассовых операций.doc

• Подбор оборудования и установление режима работы фонтанной скважины, эксплуатирующей нефтяную оторочку.docx

• Задача Списаны средства бюджета, использованные учреждением за год, в том числе на оплату труда 150000 руб.docx