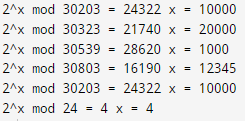ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 14
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ государственное БЮДЖЕТНОЕ
образовательное учреждение
высшего образования
«НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
_________________________________________________________________
Кафедра защиты информации

ОТЧЁТ
по лабораторной работе № 4
«Последовательные одномерные контейнеры»
по дисциплине: «Программирование»
Выполнил(а):Проверил:
Студент гр. «АБ-124»,
«АВТФ» кафедры ЗИ доцент
Белкин Г.А. Архипова А. Б.
«14» _02__ 2023 г«___» ______
_________________
_________________ ____________
(подпись) (подпись)
Новосибирск 2022
Цели и задачи работы: изучение алгоритмов формирования и обработки одномерных массивов и последовательных контейнеров, программирование и отладка программ формирования и обработки массивов.
Задание к работе: Написать программу решения задачи в соответствии с индивидуальным вариантом.
Задание 1: Отделите корни заданного уравнения, согласно варианту из табл.1, и уточните их одним из методов с точностью до ε=10-4 . Решить уравнения методом половинного деления, методом Ньютона и методом простых итераций. Либо другими методами, перечисленными в теоретической части к заданию
вариант 4: ???? ????????( ???? + 1) = 1
Метод Ньютона:
1. Задать начальные приближения х(0) так, чтобы выполнялось неравенство f(x(0))*f’’(x(0))>0, а также малое положительное число ε. Положить k=0.
2. Вычислить х(к+1) по формуле: xk+1=xk−f(xk)/f’(xk)
3. Если | xк+1 - xк| < ε процесс завершить и положить х*=х(к+1), иначе, k=k+1 и перейти к пункту 2.
Метод половинного деления:
1. Найти начальный интервал неопределенности [a0,b0]
одним из методов отделения корней, задать малое положительное число ε и присвоить k=0.
2. Найти середину текущего интервала неопределенности ск=(ak+bk)/2.
3. Если f(aк)*f(cк)<0, то положить ак+1=aк, bк+1=ск иначе ак+1=ск, bк+1=bк. В результате находится текущий интервал [aк+1,bк+1].
4. Если |bк+1-ак+1|<=ε, то процесс завершить: х*=(aк+1+bк+1)/2, иначе k=k+1 перейти к п.2.
Метод хорд:
1. Найти начальный интервал неопределенности [a0,b0] одним из методов отделения корней, выбрать х0 из этого интервала. Задать точность вычислений – малое положительное число ε и присвоить k=0.
2. Определить неподвижный конец отрезка.
3. Вычислить по рекуррентной формуле хk+1 через xk.
4. Если ????−???? ???? |????????+1 − ???????? | ≤ ????, решением уравнения - будет х*=хk+1 процесс завершить, иначе k=k+1 перейти к п.3.
C++
#include
#include
#include
using namespace std;
double F(double x) {
double f;
f = x * log(x + 1) - 1;
return f;
}
double F1(double x) {
double f1;
f1 = x / (x + 1) + log(x + 1);
return f1;
}
double F2(double x) {
double f2;
f2 = 1 / (x + 1) + 1 / (pow(x + 1, 2));
return f2;
}
double chord(double eps, double a, double b) {
double x, x0;
int k = 0;
bool stat = false;
cout << "Enter an approximate x value ";
cin >> x;
if (F2(x) * F(a) > 0) {
stat = true;
}
double m, M;
M = F1(a);
m = F1(a);
for (double i = a; i <= b; i += eps) {
if (F1(i) > M) { M = F(i); }
if (F1(i) < m) { m = F(i); }
}
cout << "M = " << M << "m = " << m << endl;
cout << setw(2) << "k" << setw(12) << "Xk" << setw(9) << "Xk+1" << setw(16) << "(Xk+1 - Xk)" << endl;
while (1) {
x0 = x;
if (stat == true) {
x = x0 - (F(x0) / (F(x0) - F(a))) * (x0 - a);
}
else if (stat == false) {
x = x0 - (F(x0) / (F(b) - F(x0))) * (b - x0);
}
cout << setw(2) << k << setw(12) << x0 << setw(12) << x << setw(14) << (x - x0) << endl;
if (abs(x - x0) <= eps) { break; }
else { k++; }
}
return x;
}
double newton(double eps) {
double x, x0, deltax;
int k = 0;
cout << setprecision(4);
cout << "Enter an approximate x value "; cin >> x;
cout << setw(2) << "k" << setw(8) << "Xk" << setw(9) << "Xk+1" << setw(18) << "(Xk+1 - Xk)" << endl;
while (1) {
x0 = x;
x = x0 - (F(x0) / F1(x0));
deltax = (x - x0);
cout << setw(2) << k << setw(10) << x0 << setw(10) << x << setw(15) << deltax << endl;
if (abs(x - x0) < eps) {
break;
}
else k++;
}
return x;
}
// double a = 1, b = 2, n = 5, h, x;
// int k = 0;
// h = (b - a) / n;
// cout << "a= " << a << endl << "b= " << b << endl << "n= " << n << endl << "h= " << h << endl;
// cout << setw(15) << "x" << setw(15) << "F(x)" << endl;
// for(x=a; x <= b; x = x + h){
// cout << setw(15) << x << setw(15) << F(x);
// if (x < b && F(x)*F(x+h) < 0) {
// cout << "Promezhutok " << x << "; " << x + h << endl;
// k++;
// }
// else {
// cout << endl;
// }
// }
// cout << "Colichestvo k = " << k << endl;
// Ответ получился [1.2: 1.4]
int main() {
double a = 1.2, b = 1.4, e = 0.0001, x;
int k;
cout << "a= " << a << endl;
cout << "b= " << b << endl;
cout << "e= " << e << endl;
if (F(a) * F(b) < 0) {
cout << "Shodimost' vipolnena" << endl;
k = 0;
cout << "|" << setw(3) << "N" << setw(3) << "|" << setw(7) << "An" << setw(7) << "|" << setw(7) << "Bn" << setw(7) << "|" << setw(5) << "Bn - An" << setw(7) << "|" << endl;
while (1) {
k++;
x = (a + b) / 2.0;
cout << "|" << setw(3) << k << setw(3) << "|" << setw(7) << a << setw(7) << "|" << setw(7) << b << setw(7) << "|" << setw(5) << b - a << setw(10) << "|" << endl;
if (abs(b - a) <= e) { break; }
if (F(a) * F(x) < 0) {
a = a;
b = x;
}
else {
a = x;
b = b;
}
}
cout << "Koren' x = " << x << endl;
cout << "Col-vo iterazii k =" << k << endl;
}
else { cout << "Uslovie ne vipolneno" << endl; }
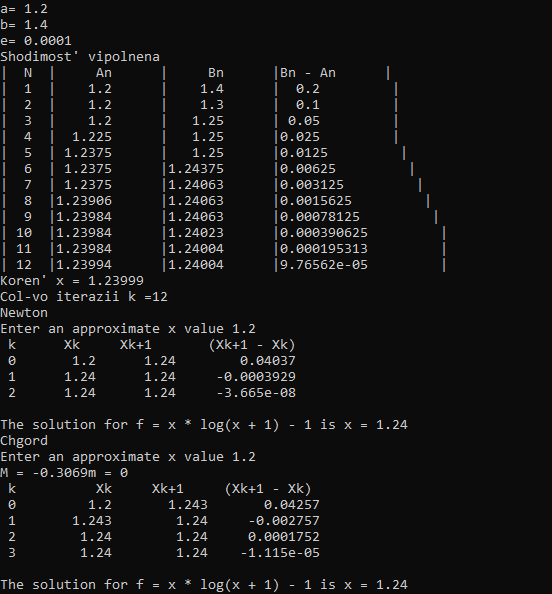
cout << "Newton" << endl;
cout << endl << "The solution for f = x * log(x + 1) - 1 is x = " << newton(e) << endl;
cout << "Chgord" << endl;
a = 0;
b = 1;
cout << endl << "The solution for f = x * log(x + 1) - 1 is x = " << chord(e, a, b);
}
Ньютон:
Python:
import math
def f(x):
F = math.exp(x) + x**2 - 2
return F
def f1(x):
F = math.exp(x) + 2*x
return F
def f2(x):
F = math.exp(x) + 2
return F
eps = 10 ** (-4)
k = 0
x = float(input("Newton's method\nEnter estimated x: "))
print('{:>3}'.format("k"), '{:>7}'.format("an"), '{:>8}'.format("an + 1"), '{:>11}'.format(" an + 1 - an"))
while True:
x0 = x
x = x0 - (f(x0) / f1(x0))
print('{:>3}'.format(k), '{:.6f}'.format(x0), '{:.6f}'.format(x), '{:.6f}'.format(x - x0))
if abs(x - x0) < eps:
break
else:
k += 1
print("The solution for e^x+x^2 = 2 is x =",'{:.6f}'.format(x))
Метод половинного деления
Python:
import math
def f(x):
F = math.exp(x) + x**2 - 2
return F
eps = 10 ** (-4)
a = 0
b = 1
k = 0
print("Half division method")
print('{:>3}'.format("k"), '{:>8}'.format("an"), '{:>7}'.format("bn"), '{:>9}'.format("bn - an"),'{:>11}'.format("(an + bn) / 2)"))
while True:
print('{:>3}'.format(k), '{:.6f}'.format(a), '{:.6f}'.format(b), '{:.6f}'.format(b - a), '{:.6f}'.format((a + b) / 2))
c = (a + b) / 2
if f(a) * f(c) < 0:
b = c
else:
a = c
if abs(b - a) <= eps:
x = (a + b) / 2
break
else:
k += 1
print("The solution for e^2+x^2 = 2 is x =", '{:.6f}'.format(x))
Метод хорд
def f(x):
F = math.exp(x) + x**2 - 2
return F
def f1(x):
F = math.exp(x) + 2*x
return F
def f2(x):
F = math.exp(x)+2
return F
eps = 10 ** (-4)
a = 0
b = 1
k = 0
print("Chord method")
print("Enter estimated x: ")
x = float(input())
if f2(x) * f(a) > 0:
stat = True
elif f2(x) * f(b) > 0:
stat = False
M = f1(a)
i = a
while i <= b:
if f1(i) > M:
M = f(i)
i += 1
m = f1(a)
i = a
while i <= b:
if f1(i) < m:
m = f(i)
i += 1
print(M, m)
print('{:>3}'.format("k"), '{:>7}'.format("an"), '{:>8}'.format("an + 1"), '{:>11}'.format(" an + 1 - an"))
while True:
x0 = x
if stat is True:
x = x0 - (f(x0) / (f(x0) - f(a))) * (x0 - a)
elif stat is False:
x = x0 - (f(x0) / (f(b) - f(x0))) * (b - x0)
print('{:>3}'.format(k), '{:.6f}'.format(x0), '{:.6f}'.format(x), '{:.6f}'.format(x - x0))
if abs(x - x0) <= eps:
break
else:
k += 1
print("The solution for e^2+x^2 = 2 is x =", '{:.6f}'.format(x))
Вариант 4: mt19937_64
1.Напишите программу, в которой определен массив из ???? целых чисел (???? ≥ 10). Инициализируйте массив случайными целыми числами из диапазонов [-300, -150] и [150, 300]. 2.Вычислите среднее арифметическое элементов массива из пункта 1, наибольший и наименьшей элементы. 3.Переставьте элементы массива из пункта 1 наоборот (дополнительный массив не используйте). Отсортируйте в порядке возрастания первую половину массива из пункта 1, а вторую – в порядке убывания. 4.Определите и инициализируйте массив, состоящий из случайных символов. Напишите программу, удаляющую из массива цифры и строчные буквы. 5.Напишите программу, в которой определены два массива и инициализированы случайными числами. Модифицируйте массивы путём циклического сдвига на один элемент влево синхронно в обоих массивах (например, даны два массива [1, 2, 3] и [4, 5, 6], после преобразования получится [2, 3, 4] и [5, 6, 1].
#include
#include
#include
#include
using namespace std;
int random(int a, int b) {
static mt19937_64 gen(time(NULL));
uniform_int_distribution<> uid(a, b);
return uid(gen);
}
void filling(int Arr[], int a, int b, int a1, int b1, int n) {
for (int i = 0; i < n / 2; i++) {
Arr[i] = random(a, b);
}
for (int i = n / 2; i < n; i++) {
Arr[i] = random(a1, b1);
}
}
void filling(int Arr[], int a, int b, int n) {
for (int i = 0; i < n; i++) {
Arr[i] = random(a, b);
}
}
void show(int Arr[], int n) {
for (int i = 0; i < n; i++) {
cout << Arr[i] << " ";
}
}
double Sredn(int Arr[], int n) {
double sr = 0;
for (int i = 0; i < n; i++) {
sr = sr + Arr[i];
}
return sr / n;
}
void MIN_MAX(int arr[], int n) {
int min = 0, max = 0;
for (int i = 0; i < n; i++)
{
if (arr[i] < min) {
min = arr[i];
}
if (arr[i] > max) {
max = arr[i];
}
}
cout << "Max is " << max << endl;
cout << "Min is " << min << endl;
}
void Sort(int arr[], int n) {
for (int i = 0; i < n / 2; i++) {
for (int j = 0; j < n / 2 - 1; j++) {
if (arr[j] > arr[j + 1]) {
int b = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = b;
}
}
}
for (int i = n / 2; i < n; i++) {
for (int j = n / 2; j < n - 1; j++) {
if (arr[j] > arr[j + 1]) {
int b = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = b;
}
}
}
}
void fillingChar(char Arr[], int n) {
for (int i = 0; i < n; i++) {
Arr[i] = random(33, 127);
}
}
void showChar(char Arr[], int n) {
for (int i = 0; i < n; i++) {
cout << Arr[i];
}
cout << endl;
}
void DeleteChar(char Arr[], int n) {
for (int i = 0; i < n; i++) {
if (Arr[i] >= 48 and Arr[i] <= 57 || Arr[i] >= 97 and Arr[i] <= 122) { Arr[i] = '!'; };
}
}
void Remove(int Arr[], int Arr1[], int a, int b) {
int x, x1, y, y1;
x = Arr[0];
x1 = Arr[a - 1];
y = Arr1[0];
y1 = Arr1[b - 1];
for (int i = 0; i < a - 1; i++) {
Arr[i] = Arr[i + 1];
}
for (int i = 0; i < b - 1; i++) {
Arr1[i] = Arr1[i + 1];
}
Arr[a - 1] = y;
Arr1[b - 1] = x;
show(Arr, a);
show(Arr1, b);
}
int main() {
int Arr[15], Arr1[3], Arr2[3];
char ArrCh[15];
filling(Arr, -300, -150, 150, 300, 15);
filling(Arr1, -300, 300, 3);
filling(Arr2, -300, 300, 3);
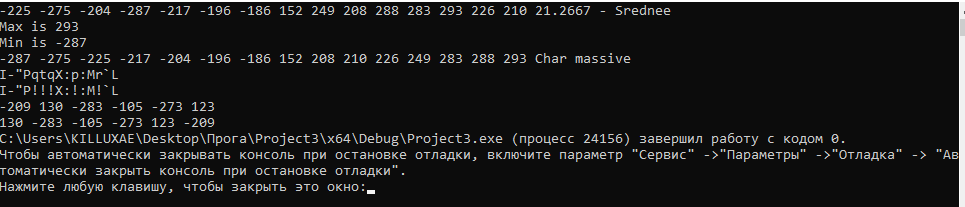
show(Arr, 15);
double sr = Sredn(Arr, 15);
cout << sr << " - Srednee" << endl;
MIN_MAX(Arr, 15);
Sort(Arr, 15);
show(Arr, 15);
fillingChar(ArrCh, 15);
cout << "Char massive" << endl;
showChar(ArrCh, 15);
DeleteChar(ArrCh, 15);
showChar(ArrCh, 15);
show(Arr1, 3);
show(Arr2, 3);
cout << endl;
Remove(Arr1, Arr2, 3, 3);
}
Задание 3:
Задание выполняется на языке C++. В соответствии с вариантом необходимо описать распределение генератора, с помощью этого генератора заполнить 3 массива размером 50, 100 и 1000 соответственно числами от 1 до 100.
Использовать критерий хи-квадрат для проверки гипотезы о нормальном распределении выборки. Значение критерия хи-квадрат для каждой из выборок рассчитывается по формуле:
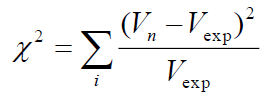
где Vn – количество элементов, попавших в i-ый интервал;
Vexp – ожидаемое число попаданий в i-ый интервал.
Проанализировать значение критерия хи-квадрат и вывести:
1) результат проверки гипотезы;
2) ожидаемое и реальное математическое ожидание.
Вариант 4: mt19937_64
C++
#include
#include
#include
#include
using namespace std;
int random(int a, int b) {
static mt19937_64 gen(time(NULL));
uniform_int_distribution<> uid(a, b);
return uid(gen);
}
void filling(int arr[], int n) {
for (int i = 0; i < n; i++) {
arr[i] = random(1, 100);
}
}
void sort(int arr[], int n) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n - 1; j++) {
if (arr[j] > arr[j + 1]) {
int b = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = b;
}
}
}
}
void show(int Arr[], int n) {
for (int i = 0; i < n; i++) {
cout << Arr[i] << " ";
}
}
int main() {
int Arr1[50], Arr2[100], Arr3[1000];
int h = 5, interval = 5, xi = 0, Vexp1 = 50 / 20, Vexp2 = 100 / 20, Vexp3 = 1000 / 20;
filling(Arr1, 50);
sort(Arr1, 50);
filling(Arr2, 100);
sort(Arr2, 100);
filling(Arr3, 1000);
sort(Arr3, 1000);
int res1[20] = { 0 }, res2[20] = { 0 }, res3[20] = { 0 };
for (int i = 0, j = 0; i < 50; i++) {
if (Arr1[i] <= interval) {
res1[j] ++;
}
else {
interval += h;
j++;
i--;
}
}
cout << endl;
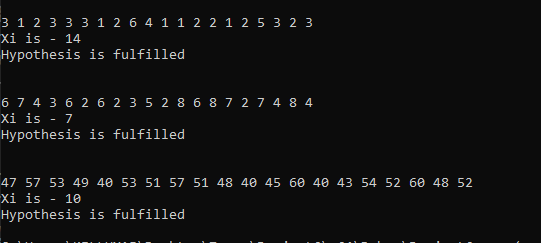
show(res1, 20);
for (int i = 0; i < 20; i++) {
xi += float((pow((res1[i] - Vexp1), 2)) / Vexp1);
}
cout << endl << "Xi is - " << xi << endl;
if (xi < 15.1) { cout << "Hypothesis is fulfilled" << endl; }
else { cout << "Hypothesis is not fulfilled" << endl; }
h = 5; interval = 5; xi = 0;
for (int i = 0, j = 0; i < 100; i++) {
if (Arr2[i] <= interval) {
res2[j] ++;
}
else {
interval += h;
j++;
i--;
}
}
xi = 0;
cout << endl;
cout << endl;
show(res2, 20);
for (int i = 0; i < 20; i++) {
xi += float((pow((res2[i] - Vexp2), 2)) / Vexp2);
}
cout << endl << "Xi is - " << xi << endl;
if (xi < 23.2) { cout << "Hypothesis is fulfilled" << endl; }
else { cout << "Hypothesis is not fulfilled" << endl; }
h = 5; interval = 5; xi = 0;
for (int i = 0, j = 0; i < 1000; i++) {
if (Arr3[i] <= interval) {
res3[j] ++;
}
else {
interval += h;
j++;
i--;
}
}
xi = 0;
cout << endl;
cout << endl;
show(res3, 20);
for (int i = 0; i < 20; i++) {
xi += float((pow((res3[i] - Vexp3), 2)) / Vexp3);
}
cout << endl << "Xi is - " << xi << endl;
if (xi < 30.6) { cout << "Hypothesis is fulfilled" << endl; }
else { cout << "Hypothesis is not fulfilled" << endl; }
}
Задание №4 «Криптографические приложения»*
Выполнить программную реализацию метода «шаг младенца, шаг великана» и алгоритма исчисления порядка и решить с помощью компьютера следующие уравнения:
1) 2x mod 30203 = 24322;
2) 2x mod 30323 = 21740;
3) 2x mod 30539 = 28620;
4) 2x mod 30803 = 16190;
5) 2x mod 30203 = 24322.
С++:
#include
#include
#include
using namespace std;
void solve(int p, int y) {
int k, m, a = 2;
k = int(sqrt(p)) + 1;
m = int(sqrt(p)) + 1;
cout << "2^x mod " << p << " = " << y;
vector
for (int exp = 1; exp < k; exp++) { // 1 ряд (a^1...a^(k*exp))
int res1 = 1;
for (int i = 1; i <= exp * m; i++) {
res1 *= a;
res1 %= p;
}
giant.push_back(res1);
}
int res2 = y;
for (int exp = 1; exp < k; exp++) { //2 ряд (y*a^1...y*a^j)
res2 *= a;
res2 %= p;
baby.push_back(res2);
}
for (int i1 = 0; i1 < giant.size(); i1++) {
for (int i2 = 0; i2 < baby.size(); i2++) {
if (giant[i1] == baby[i2]) {
cout << " x = " << (i1 + 1) * m - (i2 + 1) << endl;
return;
}
}
}
}
int main() {
solve(30203, 24322);
solve(30323, 21740);
solve(30539, 28620);
solve(30803, 16190);
solve(30203, 24322);
solve(25, 4);
}
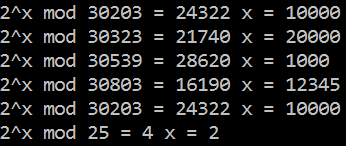
Python:
import math
def solve(p, y):
a = 2
k = math.floor(math.sqrt(p)) + 1
m = math.floor(math.sqrt(p)) + 1
print("2^x mod", p, "=", y, end = '')
giant = list()
baby = list()
for degree in range(1, k + 1):
res1 = 1
for i in range(1, degree * m + 1):
res1 *= a
res1 %= p
giant.append(res1)
res2 = y
for degree in range(1, k + 1):
res2 *= a
res2 %= p
baby.append(res2)
for i1 in range(len(giant)):
for i2 in range(len(baby)):
if giant[i1] == baby[i2]:
print(" x =", (i1 + 1) * m - (i2 + 1))
return
solve(30203, 24322)
solve(30323, 21740)
solve(30539, 28620)
solve(30803, 16190)
solve(30203, 24322)
solve(24,4)