Файл: Российской федерации ордена Трудового Красного Знамени федеральное государственное.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 23
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И ИНФОРМАТИКИ
Кафедра общая теория связи
Лабораторная работа 20А
“Эффективное кодирование”
по дисциплине
Общая теория связи
Выполнил:
Студент гр. БСС1952
Проверил:
Ассистент
Кудряшова Анастасия Юрьевна
Москва, 2021
Цель работы:
Изучить основные способы увеличения энтропии дискретного источника и принципы эффективного кодирования.
Задание 1.
Задан дискретный источник двоичных сообщений, который производит слова, состоящие из двух букв А и М. Всего возможно четыре различных сообщения,слова: АА, AM, МА, ММ. Рассчитайте вероятность каждого слова р(АА), р(АМ), р(МА), р(ММ), если заданы (см. таблицу А) безусловные вероятности р(А), р(М) и условные вероятности.
(р(А/М) - вероятность буквы A, если первой в слове была буква М; остальные обозначения аналогичны).
P(A) = 0.7 > >> P(M) = 1-P(A) = 0.3
P(A/M)=0.4 > (PM/M) = 1-P(A/M) = 0.6
P(M/A)-= 0.2 > P(AA) = 1 –P(M/A) = 0.8
Вероятности появления каждого слова равны:
Слово AA: P(AA) =P(A) *P(A/A)=0.7 *0.8 = 0,56
Слово AM: P(AM) = P(A) * P(M/A) = 0.7 * 0.2 = 0,14
Слово MA: P(MA) = P(M) * P(A/M) = 0.3 * 0.4 = 0,12
Слово MM: P(MM) = P(M) * P(M/M) = 0,3 * 0,6 = 0,18
Задание 2.
Рассчитайте энтропию источника Н и его избыточность R.
Так как слова независимы, то энтропию источника можно посчитать как энтропию источника независимых слов. Но, для определения энтропии на букву источника, полученный результат следует разделить на количество букв в слове, то есть на 2:
Где p(Si) – вероятность i-гo слова;
m - общее количество слов (в данном случае m= 4);
n -количество букв в слове (в данном случае n = 2);
lg - десятичный логарифм.
Т.е:
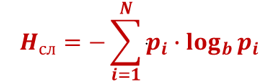
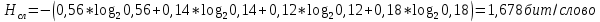
Тогда энтропия на один символ равна:
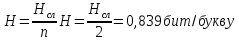
Избыточность источника X равна:
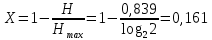
Задание 3.
Закодируйте слова четверичным кодом и рассчитайте его энтропию и избыточность.
СЛОВО AA > 0: P(0) = P(AA) = 0,56
СЛОВО AM > 0: P(1) = P(AM) = 0,14
СЛОВО MA > 0: P(2) = P(MA) = 0,12
СЛОВО MM > 0: P(3) = P(MM) = 0,18
Символы независимы, то энтропия равна:
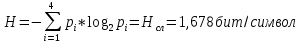
Избыточность источника X равна:
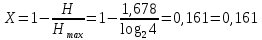
Задание 4.
Закодируйте четыре слова безызбыточным кодом с префиксными свойствами, построив кодовое дерево.Рассчитайте энтропию нового двоичного кода, его избыточность и среднюю длину кодовой комбинации.
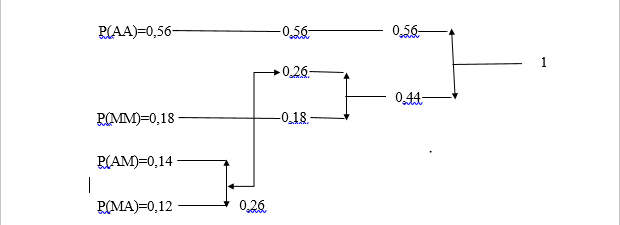
Слово AA > 1: длина слова n1=1
Слово MM >00: длина слова n2 = 2
Слово AM > 011: длина слова n3=3
Слово MA > 010: длина слова n4=3
Из 100 среднестатистических сообщений получаем :
AA – 56 раз комбинация 1
MM – 18 раз комбинация 00
AM – 14 раз комбинация 011
MA – 12 раз комбинация 010
Количество встречаемых 0 и 1 и их вероятности:
N0 = 18 * 2 + 14 * 1 + 12 * 2 = 74; N1= 56 * 1 + 14 *2 + 12 *1 = 96
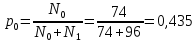 ;
;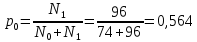
Энтропия кода равна:
Избыточность источника X:
Средняя длина кодовой комбинации равна:
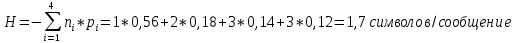
Задание 5.
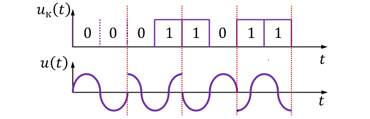
Запишите выражения, соответствующие передаче нуля и единицы с помощью двоичной фазовой модуляции. Запишите выражения, соответствующие передаче различных комбинаций из двух символов, «дибитов», с помощью четырехпозиционной ФМ. Нарисуйте временные диаграммы сигналов двоичной и четырехпозиционной ФМ.
Определите максимальное значение энтропии для m=2 и m=4.
Выражения, соответствующие передачу нуля и единицы с помощью ДФМ:
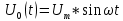
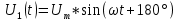
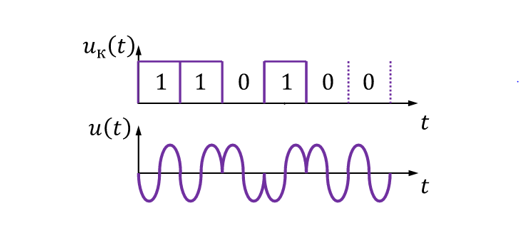
Выражения, соответствующие передаче различных комбинаций из двух символов (“дибитов”) с помощью четырехпозиционной ФМ:
00>0;
01>1;
10>2;
11>3;
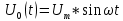
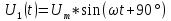
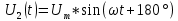
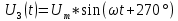
Максимальное значение энтропии для m = 2 и m = 4;
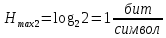
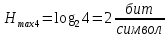
Список литературы
-
Зюко А.Г., Кловский Д.Д., Назаров М.В., Коржик В.И. Теория электрической связи. – М.: Радио и связь, 1998. -
Зюко А.Г., Кловский Д.Д., Назаров М.В.,Финк Л.М. Теория передачи сигналов. – М.: Радио и связь, 1988.