Поурочный план или краткосрочный план для педагога организаций среднего образования

Правильные многоугольники, их свойства и симметрии.

Раздел: геометрия	Раздел 9.4А Окружность. Многоугольники
ФИО педагога	Оспанов А.С.
Дата:	19.04.2023
Класс: 9	Количество присутствующих:		Количество отсутствующих:
Тема урока	Правильные многоугольники, их свойства и симметрии .Урок 1.
Цели обучения в соответствии с учебной программой		9.1.2.1 знать и применять свойства и признаки вписанных и описанных четырёхугольников;
Цели урока	знает и применяет свойства и признаки вписанных и описанных четырехугольников

Ход урока

Этапы	Действия педагога	Действия учени	Оценивание	Ресурсы
Начало урока	1. Организационный момент: Приветствие, проверка готовности к уроку. 2. Проверка предварительных знаний. Цель: повторить пройденный материал необходимый для новой темы Фронтальный опрос Центр вписанной в треугольник окружности – точка пересечения его …(биссектрис) Центр вписанной в треугольник окружности равноудален от его …(сторон) Многоугольник называется вписанным в окружность, если все его …(вершины лежат на окружности) Окружность вписана в многоугольник, если …(все его стороны касаются окружности) Вписанные углы равны, если они…(опираются на одну дугу) Центр описанной около треугольника окружности равноудален от его …(вершин) Постановка проблемы. - Можно ли в окружность вписать четырехугольник? Всегда ли это можно сделать? А описать около окружности четырехугольник? - Давайте попробуем вместе сформулировать цель нашего урока.	Настрой на урок отвечает на вопросы формули руют цель урока	за правильны ответ раздаются жетоны ответившим ученикам	Презентация
Середина урока	Введение в новую тему. Цель: с помощью практических заданий учащиеся сами выводят свойства вписанного четырехугольника Разделим страничку на 2 половинки, выполняем построение. Отметим на окружности четыре точки, и соединим их хордами. Получили четырехугольник, вписанный в окружность. Попробуйте сформулировать определение вписанного четырехугольника. Четырехугольник, все вершины которого лежат на окружности, называется вписанным в эту окружность, а окружность – описанной.) На другой окружности отметим 4 точки и проведем через них отрезки касательных. Получили четырехугольник, описанный около окружности. Попробуйте сформулировать определение описанного четырехугольника. (Четырехугольник, все стороны которого касаются окружности, называется описанным около этой окружности. 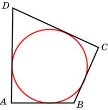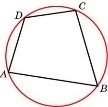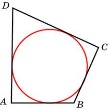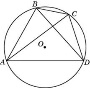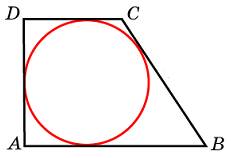А окружность – вписанной в этот четырехугольник.) Свойства вписанного четырехугольника и его признак связаны с углами этого четырехугольника. Теорема (свойство углов вписанного четырехугольника) Сумма противоположных углов вписанного четырехугольника равна 180°. 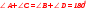- всегда ли можно вписать четырехугольник в окружность? (нет) - попробуйте сформулируйте теорему обратную? Если …., то… Это будет признаком вписанного четырехугольника Если в четырехугольнике сумма двух противоположных углов равна 180°, то около такого четырехугольника можно описать окружность. Свойство описанного четырехугольника и его признак связаны со сторонами этого четырехугольника. Теорема (свойство сторон описанного четырехугольника) Суммы противоположных сторон описанного четырехугольника равны. AB+CD=DC+AD - Всегда ли можно описать четырехугольник около окружности? (нет) - Попробуйте сформулировать теорему обратную? Если …., то… Если в четырехугольнике суммы противоположных сторон равны, то в этот четырехугольник можно вписать окружность. - Перечислите виды четырехугольников. - Какие из них можно вписать в окружность? Почему? Объясните ответ? (Из всех параллелограммов только около прямоугольника можно описать окружность. Около трапеции можно описать окружность только тогда, когда она равнобедренная.) (В любой ромб можно вписать окружность. Если в параллелограмм вписана окружность, то он является ромбом	формулируют свойства вписанного четырех угольника Выполняют построение по алгоритму Записывают в тетрадь	похвала, обратная связь
Закрепление новой темы	5. Решение задач. Фронтальная работа 1) В четырехугольник ABCD вписана окружность, AB = 11, CD = 17. Найдите периметр четырехугольника.(56 см) 2) ABCD- вписанный четырёхугольник, один из углов в 2 раза больше другого. Найти эти углы (60, 120) 3) В равнобедренную трапецию вписали окружность, которая делит боковую сторону на отрезки в отношении 9:16. Найти длины этих отрезков, если средняя линия трапеции равна 50 см. (сумма оснований 100 см , 2(9х+16х)=100, х=2 , ответ: 18 см и 32 см) 4) Найти периметр равнобедренной трапеции, диагональ которой перпендикулярна боковой стороне и образует с основанием угол 30 градусов, если радиус окружности, описанной около трапеции, равен 8 см.(16+8+8+8=40 см)	Вполняют задание, обсуждают в классе	Взаимопро верка за каждое правильное решение жетон	Карточки презентация
Индивидуальная работа.	1. В четырехугольник ABCD вписана окружность, AB = 10, BC = 11 и CD = 15. Найдите четвертую сторону четырехугольника. Ответ: ___________ 2. Два угла вписанного в окружность четырехугольника равны 84° и 57°. Найдите меньший из оставшихся углов. Ответ дайте в градусах. Ответ: ___________ 3. В четырехугольник ABCD вписана окружность, AB = 10, CD = 16. Найдите периметр четырехугольника.    Ответ: ___________ 4. Четырехугольник ABCD вписан в окружность. Угол ABD равен 75°, угол CADравен 35°. Найдите угол ABC. Ответ дайте в градусах. Ответ: ___________ 5. Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности. Ответ: ___________ Ответы:1) 14, 2) 96°, 3) 52, 4) 110°, 5) 2.	Вполняют задание, обсуждают в классе	за каждое правильное решение жетон
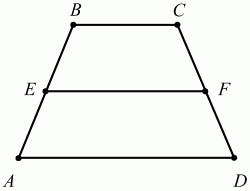
Конец урока Домашнее задание	Дифференцированные задания Уровень А Задача 1. Найдите все углы вписанного в окружность четырехугольника АВСD, если ∠ А=40º, а ∠D =90º Ответ: ∠С = 140°, ∠B= 90° Задача 2. Противоположные стороны четырехугольника, описанного около окружности, равны 7 см и 10 см. Можно ли по этим данным найти периметр четырехугольника? Ответ: Да, 34 см. Уровень В Известно, что в трапецию ABCD с основаниями AD и ВС можно вписать окружность и около неё можно описать окружность, EF – её средняя линия. Известно, что АВ + CD + EF = 18. Найдите периметр трапеции (1) Ответ: 24.		Подсчет жетонов перевод в 10 бальную систему, оценка за урок
Рефлек сия	Рефлексия. 1.На уроке я работал……..потому что……… 2.Своей работой на уроке я……… 3.Урок для меня показался……. 4.За урок я….. 5.Мое настроение…….. 6.Материал урока мне был………

---

---

Смотрите также файлы

• Основными принципами арбитражного процесса являются независимость судей.docx

• Бланк выполнения лабораторной работы 1 Опыт Юнга.docx

• Занятие 1 Задание Перечислите основные принципы устройства государственных и муниципальных финансов, раскройте их содержание.docx

• 2. 1 Анализ использования основных средств 7.docx

• Текст повествование.pptx