Федеральное агентство связиФедеральное государственное бюджетное образовательное учреждение высшего образования «Сибирский государственный университет телекоммуникаций и информатики»(СибГУТИ)Лабораторная работа № 1«Исследование реактивных двухполюсников»По дисциплине: Теория электрических цепейВыполнила: Кувалдина А.Е.Группа: ЗБТ-12Вариант: 09Проверил: Черных Ю.С.Новосибирск, 2023 гЛабораторная работа № 1«Исследование реактивных двухполюсников»

1. 
   Цель работы: Исследование зависимости входного сопротивления реактивного двухполюсника от частоты.
   

2. 
   Подготовка к выполнению работы
   

При подготовке к работе необходимо изучить теорию реактивных двухполюсников, методы их анализа и синтеза (см. раздел «Теория» параграфы 4.5 и 16.6).

3. 
   Теоретическое исследование
   

1. 
   Исследовать работу схемы реактивного двухполюсника, реализованного по 1-й форме Фостера (рисунок 1.1, а).
   

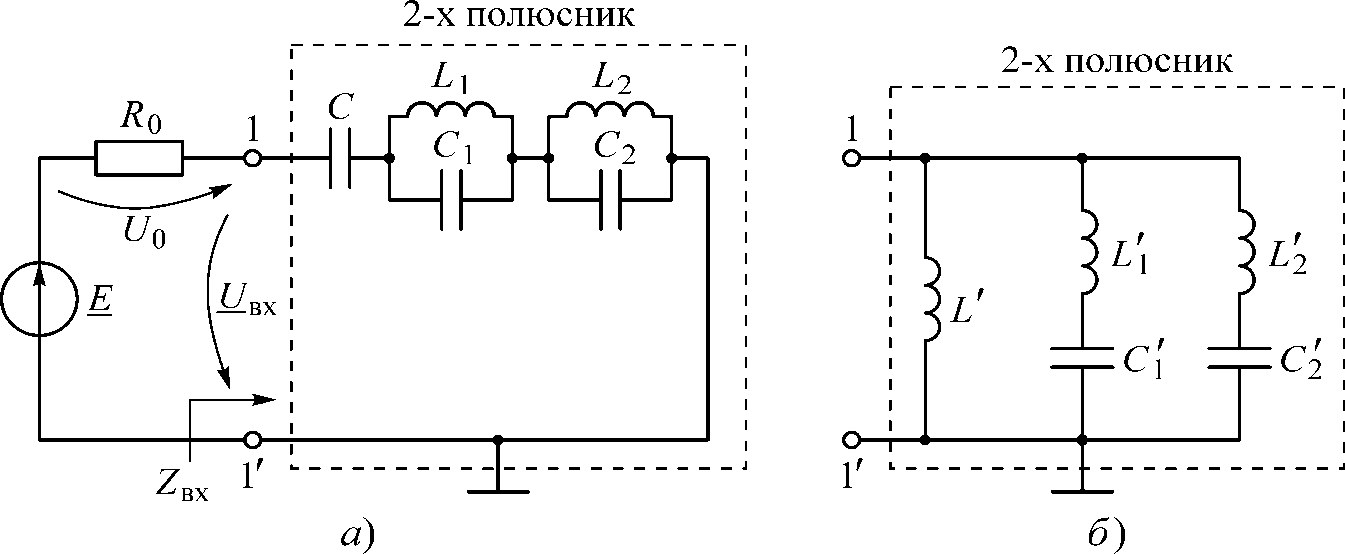
Задать E= 1 В, R₀ = 10 кОм, L₁ = L₂ = 1 мГн, C₁ = 63,536 нФ, С₂ = 15,831 нФ, С = (100+Nx5) нФ, где N- номер варианта (последняя цифра пароля).Рисунок 1.1 – Схемы реактивных двухполюсников

2. 
   Определить частоты резонансов напряжений и токов схемы 2-х полюсника (рис 1.1, а). Для определения резонансных частот необходимо рассчитать нули и полюсы выражения эквивалентного сопротивления схемы Z_экв.(jω).
   

Таблица 1.1 – Резонансные частоты 2-х полюсников

Вид схемы	Резонансы напряжений		Резонансы токов
	ωрез. , рад/с	, кГц	ωрез. , рад/с	, кГц
Схема а
Схема б

---

3. 
   В диапазоне частот 0,1 мГц – 80 кГц на частотах резонансов и по одной частоте между резонансами рассчитать входное сопротивление Z_вх(f) и записать в таблицу 1.2 его значения.
   

Таблица 1.2 – Частотная характеристика двухполюсника

f, кГц	f1	f2	fрез1	f4	fрез2	f6	fрез3	f8	fрез 4	f10	f11
	0										80
Zвх

4. 
   Записать выражение Z_экв.(jω) через резонансные частоты
   
5. 
   Рассчитать параметры элементов обратного двухполюсника (рисунок 1.1, б) по формулам:
   

6. 
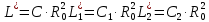
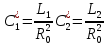
   Рассчитать входное сопротивление Z_вх.(f) обратного двухполюсника (рисунок 1.1, б) и записать в таблицу, аналогичную таблице 1.2.
   
7. 
   По результатам расчета построить в масштабе и с учетом знака реактивности графики зависимости входного сопротивления исходного и обратного реактивных двухполюсников от частоты и указать на них частоты резонансов напряжений и токов.
   

3. 
   Экспериментальная часть
   

1. 
   Исследовать работу схемы реактивного двухполюсника, реализованного по 1-й форме Фостера (рисунок 1.1, а).
   

Задать E = 1 В, R0 = 10 кОм, L1 = L2 = 1 мГн, C1 = 63,536 нФ, С2 = 15,831 нФ, С = (100+Nx5) нФ,

---

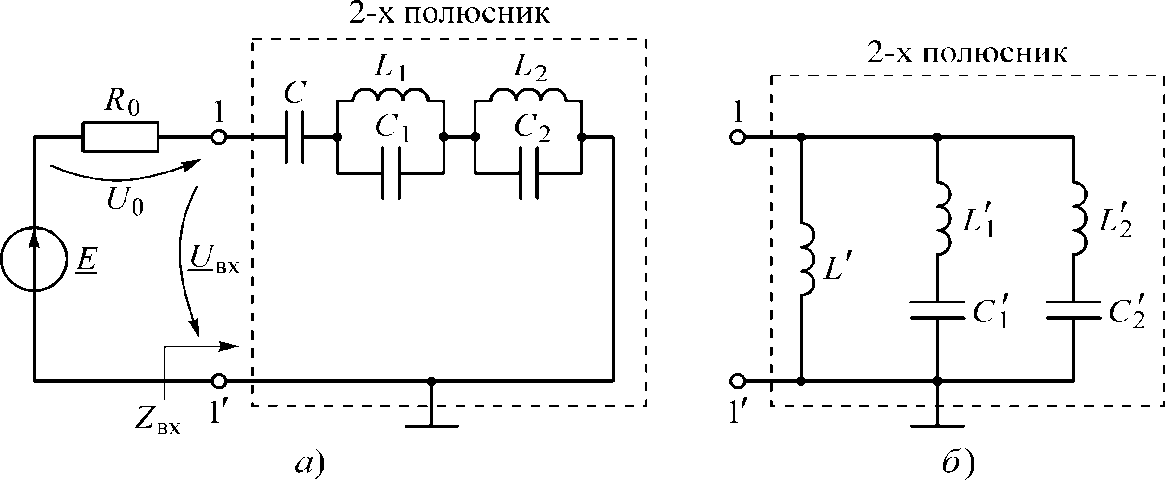
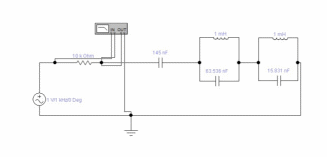
где N- номер варианта (последняя цифра пароля).С = (100+9x5) = 145 нФРисунок 1.1 – Схемы реактивных двухполюсниковВоспользуемся программой моделирования Electronics Workbench (EWB).Соберем схему, представленную на рисунке 1.1, а с учетом исходных значений элементов.Схема, собранная в EWB представлена на рисунке 1.2.Рисунок 1.2 – Схема в программе EWBПолучили частотную характеристику (см. 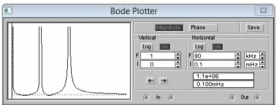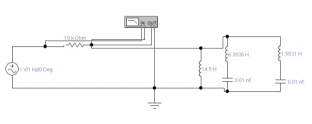рисунок 1.3).Рисунок 1.3 – Частотная характеристика H(f)=U_вх(f)/U₀(f)Соберем схему, представленную на рисунке 1.1, б с учетом исходных значений элементов.Схема, собранная в EWB представлена на рисунке 1.4.Рисунок 1.4 – Схема в программе EWBПолучили частотную характеристику (см. 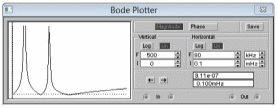рисунок 1.5).Рисунок 1.5 – Частотная характеристика H(f)=U_вх(f)/U₀(f)

2. 
   Определить частоты резонансов напряжений и токов схемы 2-х полюсника (рис. 1.1, а). Для определения резонансных частот необходимо рассчитать нули и полюсы выражения эквивалентного сопротивления схемы Zэкв.(jω).
   

Таблица 1.1 – Резонансные частоты 2-х полюсников

Вид схемы	Резонансы напряжений		Резонансы токов
	ωрез. , рад/с	, кГц	ωрез. , рад/с	, кГц
Схема а	60318,58 и 165876,1	9,6 и 26,4	125663,71 и 251327,41	20 и 40
Схема б	125663,71 и 251327,41	20 и 40	60318,58 и 165876,1	9,6 и 26,4

1.3. В диапазоне частот 0,1 мГц – 80 кГц на частотах резонансов и по одной частоте между резонансами рассчитать входное сопротивление Zвх(f) и записать в таблицу 1.2 его значения

---

Таблица 1.2

f, кГц	f1	f2	fрез1	f4	fрез2	f6	fрез3	f8	fрез 4	f10	f11
	0	5,149	8,8	12,8	20	22,4	25,6	28,8	40	60	80
Zвх, Ом	1,1*10^10	147	2	140	37700	388	20,3	1700	9150000	367	215

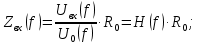
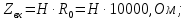
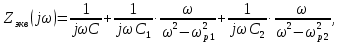
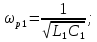
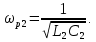
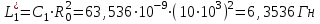
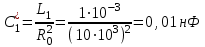
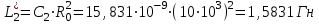
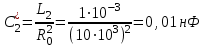
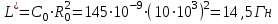
1.4. Записать выражение Zэкв.(jω) через резонансные частотыВходное сопротивление Zвх в таблице 1.2 вычисляем косвенным методом, воспользовавшись формулой:где 1.5. Рассчитать параметры элементов обратного двухполюсника (рисунок 1.1, б) по формулам:1.6. Рассчитать входное сопротивление Zвх.(f) обратного двухполюсника (рисунок 1.1, б) и записать в таблицу, аналогичную таблице 1.2.Таблица 1.3

f, кГц	f1	f2	fрез1	f4	fрез2	f6	fрез3	f8	fрез 4	f10	f11
	0	5,149	8,8	12,8	20	22,4	25,6	28,8	40	60	80
Zвх, Ом	9,11*10-3	698*103	397*105	697*103	287*102	316*103	594*104	556*103	10,9	274*103	468*103

---

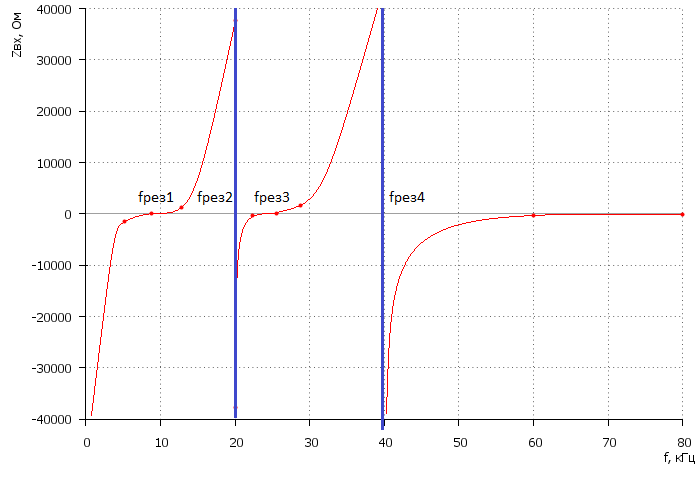
1.7. По результатам расчета построить в масштабе и с учетом знака реактивности графики зависимости входного сопротивления исходного и обратного реактивных двухполюсников от частоты и указать на них частоты резонансов напряжений и токов.График зависимости модуля входного сопротивления исходного реактивного двухполюсника от частоты представлен на рисунке 1.6.Рисунок 1.6 – График зависимости Z_вх(f):fрез1 и fрез3 – резонансы напряжений;fрез2 и fрез4 – резонансы токов.График зависимости модуля входного сопротивления обратного реактивного двухполюсника от частоты представлен на рисунке 1.7.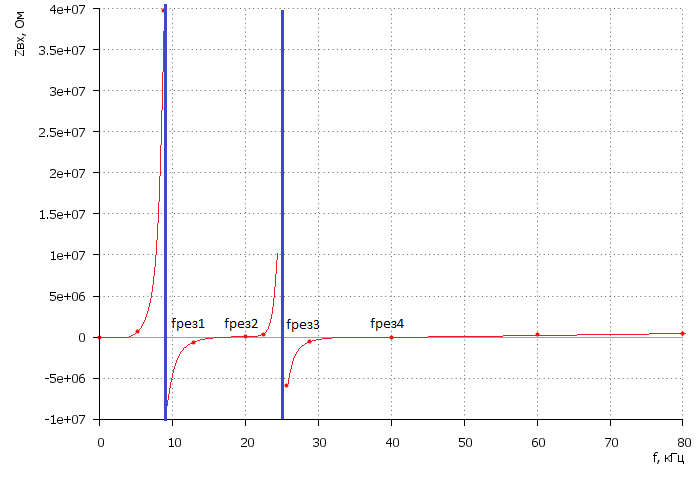Рисунок 1.7 – График зависимости Z_вх(f):ВыводПри выполнении лабораторной работы было проведено исследование зависимости входного сопротивления реактивного двухполюсника (исходного и обратного) от частоты.Выяснили, что:1) Входное сопротивление растет с ростом частоты;2) Количество резонансных частот на единицу меньше числа элементов;3) Резонансы токов (полюса Z(jω)) и напряжений (нули Z(jω)) чередуются, причем, если входное сопротивление двухполюсника на нулевой частоте равно нулю, то первым наступает резонанс токов.

---

Смотрите также файлы

• Л. Н. Гумилев атындаы Еуразия лтты университеті Апаратты технологиялар факультеті Апаратты жйелер кафедрасы Мліметтер оры бойынша Реферат.docx

• Лекция Введение.doc

• Отчет о производственной практике практика по профилю специальности.docx

• Технология получения мяса индеек.rtf

• Анатомия центральной нервной системы Практическое задание 2.docx