ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 87
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Подготовка к ЕГЭ
Закон радиоактивного распада
Задание № 1
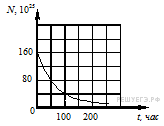
№ 1. Дан график зависимости числа не распавшихся ядер эрбия от времени. Каков период полураспада этого изотопа эрбия?
1) 25 часов;
2) 50 часов;
3) 100 часов;
4) 200 часов.
№ 2. В начальный момент времени было 1 000 атомных ядер изотопа с периодом полураспада 5 минут. Сколько ядер этого изотопа останется нераспавшимися через 10 минут?
1) 0;
2) точно 250;
3) примерно 250;
4) примерно 750.
№ 3. В образце, содержащем большое количество атомов углерода 14C6, через 5 700 лет останется половина начального количества атомов. Это означает, что период полураспада ядер атомов углерода составляет:
1) 11 400 лет;
2) 5 700 лет;
3) 2 850 лет;
4) 14 лет.
№ 4. Период полураспада ядра атома:
1) зависит от времени;
2) зависит от внешних условий;
3) зависит от времени и от внешних условий;
4) не зависит ни от времени, ни от внешних условий.
№ 5. Период полураспада ядер атомов мышьяка составляет 26 ч. Это означает, что в препарате мышьяка 72As33 начальной массой 1 г:
1) примерно половина изначально имевшихся ядер мышьяка распадается за 26 ч;
2) за 26 ч массовое число каждого ядра мышьяка уменьшится вдвое;
3) все изначально имевшиеся ядра мышьяка распадутся через 52 ч;
4) одно ядро мышьяка из всех изначально имевшихся ядер распадается каждые 26 ч.
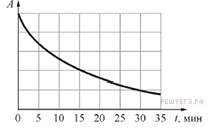
№ 6. На рисунке представлен график зависимости активности A радиоактивного источника от времени t. В момент начала наблюдения активность в 5 раз превышает безопасную. Через какое время от начала наблюдения активность достигнет безопасного значения?
1) 5 мин;
2) 15 мин;
3) 25 мин;
4) 30 мин.
Подготовка к ЕГЭ
Закон радиоактивного распада
Задание № 2
№ 1. Сколько процентов ядер некоторого радиоактивного элемента останется через время, равное трем периодам полураспада этого элемента?
1) 12,5%;
2) 0,125%;
3) 33,3%;
4) 80%.
№ 2. Период полураспада ядер атомов кобальта 60Со27 составляет 5,2 года. Это означает, что в образце, содержащем большое число атомов кобальта,
1) все изначально имевшиеся атомы распадутся через 10,4 года;
2) половина начального количества атомов распадется за 5,2 года;
3) половина начального количества атомов распадется за 2,6 года;
4) все изначально имевшиеся атомы распадутся через 5,2 года.
№ 3. Период полураспада ядер изотопа неона 25Ne10 составляет 1,2 с. Это означает, что в препарате 25Ne10 начальной массой 1 г:
1) каждое ядро 25Ne10 наполовину распадётся за 1,2 с;
2) примерно половина изначально имевшихся ядер 25Ne10 распадается за 1,2 с;
3) все изначально имеющиеся ядра изотопа неона 25Ne10 распадаются за 2,4 с;
4) для полного распада каждого ядра 25Ne10 требуется 1,2 с.

№ 4. Дан график зависимости числа не распавшихся ядер эрбия от времени. Каков период полураспада этого изотопа эрбия?
1) 25 часов;
2) 50 часов;
3) 100 часов;
4) 200 часов.
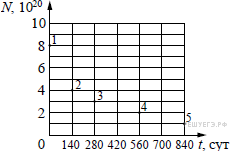
№ 5. Ядра полония 210Po84 испытывают α-распад с периодом полураспада 140 дней. В момент начала наблюдения в образце содержится 8·1020 ядер полония. Через какую из точек, кроме точки 1, пройдёт график зависимости от времени числа ещё не испытавших радиоактивного распада ядер полония?
1) 1;
2) 2;
3) 3;
4) 4.
№ 6. В образце, содержащем большое количество атомов стронция 90Sr38, через 28 лет останется половина начального количества атомов. Это означает, что период полураспада ядер атомов стронция составляет:
1) 28 лет;
2) 56 лет;
3) 14 лет;
4) 38 лет.
Подготовка к ЕГЭ
Закон радиоактивного распада
Задание № 3
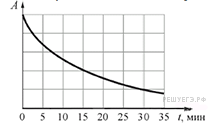
№ 1. На рисунке представлен график зависимости активности A радиоактивного источника от времени t. Через 15 минут после начала наблюдения активность достигла безопасного для человека значения. Во сколько раз активность в момент начала наблюдения превышала безопасную?
1) в 1,5 раза;
2) в 2,5 раза;
3) в 3 раза;
4) в 5 раз.
№ 2. Период полураспада ядер атомов радона 219Rn90 составляет 3,9 с. Это означает, что:
1) за 3,9 с атомный номер каждого ядра 219Rn90 уменьшится вдвое;
2) половина исходного большого количества ядер 219Rn90 распадется за 3,9 с;
3) одно ядро 219Rn90 распадается каждые 3,9 с;
4) все изначально имевшиеся ядра 219Rn90 распадутся за 7,8 с.
№ 3. Какая доля радиоактивных ядер распадается через интервал времени, равный половине периода полураспада? Ответ приведите в процентах и округлите до целых.
1) 100%;
2) 75%;
3) 50%;
4) 29%.
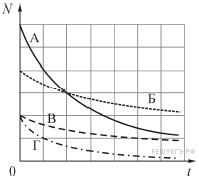
№ 4. На рисунке приведены графики зависимости числа N радиоактивных атомов от времени t для четырёх радиоактивных элементов. Наименьшим периодом полураспада обладает элемент:
| 1) А | 2) Б | 3) В | 4) Г |
№ 5. Период полураспада изотопа натрия 22Na11 равен 2,6 года. Если изначально было 104 г этого изотопа, то сколько примерно его будет через 5,2 года?
1) 13 г;
2) 26 г;
3) 39 г;
4) 52 г.
№
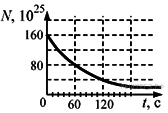 6. На рисунке приведён график зависимости числа нераспавшихся ядер эрбия 173Er68 от времени. Каков период полураспада этого изотопа?
6. На рисунке приведён график зависимости числа нераспавшихся ядер эрбия 173Er68 от времени. Каков период полураспада этого изотопа?1) 60 c;
2) 160 c;
3) 120 c;
4) 25 c.
Подготовка к ЕГЭ
Закон радиоактивного распада
Задание № 4
№ 1. Какая доля от большого количества радиоактивных атомов остается нераспавшейся через интервал времени, равный двум периодам полураспада.
1) 25%;
2) 50%;
3) 75%;
4) 0%.
№
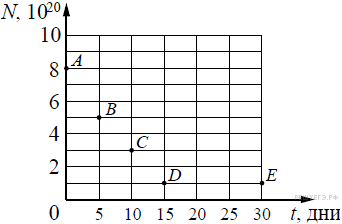 2. Ядра висмута 210Bi83 испытывают β–-распад с периодом полураспада 5 дней. В момент начала наблюдения в образце содержится 8·1020 ядер висмута. Через какую из точек, кроме точки А, пройдёт график зависимости от времени числа ядер радиоактивного висмута в образце?
2. Ядра висмута 210Bi83 испытывают β–-распад с периодом полураспада 5 дней. В момент начала наблюдения в образце содержится 8·1020 ядер висмута. Через какую из точек, кроме точки А, пройдёт график зависимости от времени числа ядер радиоактивного висмута в образце?1) С;
2) E;
3) B;
4) D.
№ 3. Период полураспада ядер франция 221Fr87 составляет 4,8 мин. Это означает, что:
1) за 4,8 мин атомный номер каждого атома франция уменьшится вдвое;
2) каждые 4,8 мин распадается одно ядро франция;
3) все изначально имевшиеся ядра франция распадутся за 9,6 мин;
4) половина изначально имевшихся ядер франция распадается за 4,8 мин.
№ 4. В образце, содержащем большое количество атомов тория 227Th90, через 19 суток останется половина начального количества атомов. Это означает, что период полураспада ядер атомов тория составляет:
1) 38 суток;
2) 9,5 суток;
3) 90 суток;
4) 19 суток.
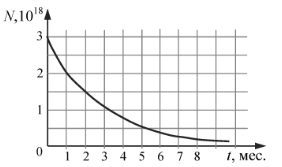
№ 5. На рисунке приведён график изменения числа ядер находящегося в пробирке радиоактивного изотопа с течением времени. Период полураспада этого изотопа:
1) 1 месяц;
2) 2 месяца;
3) 4 месяца;
4) 8 месяцев.
№
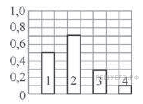 6. Доля атомов радиоактивного изотопа, распавшихся по прошествии интервала времени, равного половине периода полураспада, обозначена на гистограмме цифрой:
6. Доля атомов радиоактивного изотопа, распавшихся по прошествии интервала времени, равного половине периода полураспада, обозначена на гистограмме цифрой:1) 1;
2) 2;
3) 3;
4) 4.
Подготовка к ЕГЭ
Закон радиоактивного распада
Ответы
Задание № 1
№ 1. Период полураспада — это время, в течение которого распадается половина наличного числа радиоактивных атомов. Из графика видно, что число нераспавшихся ядер эрбия уменьшается вдвое за 50 часов. Это и есть искомый период полураспада.
Правильный ответ: 2.
№ 2. Согласно закону радиоактивного распада, по истечении времени t от первоначального количества атомов радиоактивного вещества N0 с периодом полураспада T останется примерно N=N0·2-t/T атомов. Таким образом
N=1000·2-10/5=250.
Надо понимать, что закон радиоактивного распада является законом статистическим, а не точным, поэтому он с самого начала дает только приблизительное значение. Следовательно, по истечении 10 минут останется примерно 250 атомов радиоактивного изотопа.
Правильный ответ: 3.
№ 3. Период полураспада — это время, в течение которого распадается половина наличного числа радиоактивных атомов. Поскольку в образце, содержащем большое количество атомов углерода 14С6, через 5 700 лет останется половина начального количества атомов, заключаем, что период полураспада ядер атомов углерода составляет 5 700 лет.
Привальный ответ: 2.
№ 4. Период полураспада ядра атома — это время, за которое распадается половина имеющихся ядер данного атома. Период полураспада является характеристикой конкретного атома, поэтому не зависит ни от времени, ни от внешних условий.
Правильный ответ указан под номером 4.
№ 5. Период полураспада — это время, в течение которого распадается приблизительно половина наличного числа радиоактивных атомов. Верным является утверждение, что примерно половина изначально имевшихся ядер атомов мышьяка 72As33 распадется за 26 ч.
Правильный ответ: 1.
№ 6. Из графика видно, что активность достигнет безопасного значения через 30 минут после начала наблюдения.
Правильный ответ указан под номером: 4.
Подготовка к ЕГЭ
Закон радиоактивного распада
Ответы
Задание № 2
№ 1. Согласно закону радиоактивного распада, от первоначального количества радиоактивных ядер N0 к моменту времени t должно остаться примерно N(t)=N0·2-t/T, где T — период полураспада. Следовательно, к моменту времени, равному трем периодам полураспада, ядер останется приблизительно
(N(3T)/N0)·100% = 2-3T/T ·100% = 12,5%.
Правильный ответ: 1.
№ 2. Период полураспада — это время, в течение которого распадается половина наличного числа радиоактивных атомов. Верным является утверждение, что половина начального количества атомов кобальта 60Со27 распадется за 5,2 года.
Ответ: 2.
№ 3. Период полураспада — это время, в течение которого распадается приблизительно половина наличного числа радиоактивных атомов. Верным является утверждение, что примерно половина изначально имевшихся ядер изотопа неона 25Ne10 распадется за 1,2 с.
Правильный ответ: 2.
№ 4. Период полураспада — это время, в течение которого распадается половина наличного числа радиоактивных атомов. Из графика видно, что число нераспавшихся ядер эрбия уменьшается вдвое за 50 часов. Это и есть искомый период полураспада.
Правильный ответ: 2.
№ 5. Количество ядер меняется со временем по закону N(t)=N0·2-t/T, где N0 - количество атомов в начале наблюдения, t - время прошедшее от начала наблюдения и T - период полураспада. Рассчитаем количество ядер для каждого момента времени, отмеченного на графике:
N(140) = 8·1020·2-140/140 = 4·1020 ядер;
N(280) = 8·1020·2-280/140 = 2·1020 ядер;
N(560) = 8·1020·2-560/140 = ½·1020 ядер;
N(840) = 8·1020·2-840/140 = 1/8·1020 ядер.
Из рисунка видно, что график пройдёт через точку 2.
Правильный ответ указан под номером: 2.
№ 6. Период полураспада - это время, в течение которого распадается половина наличного числа радиоактивных атомов. Поскольку в образце, содержащем большое количество атомов стронция 90Sr38, через 28 лет останется половина начального количества атомов, заключаем, что период полураспада ядер атомов стронция составляет 28 лет.
Привальный ответ: 1.
Подготовка к ЕГЭ
Закон радиоактивного распада
Ответы
Задание № 3
№ 1. Из графика видно, что активность в момент начала наблюдения была в 2,5 раза больше безопасной.
Правильный ответ указан под номером: 2.
№ 2. Период полураспада — это время, в течение которого распадается половина наличного числа радиоактивных атомов. Верным является утверждение, что половина исходного большого количества ядер 219Rn90 распадется за 3,9 с.
Правильный ответ: 2.
№ 3. Согласно закону радиоактивного распада, по истечении времени t=T/2 от первоначального количества радиоактивных атомов N0 останется примерно
N=N0·2-t/T = N0·2-½ = N0/√2.
Тем самым доля ядер, не претерпевших радиоактивного распада, составит (N/N0)·100% = (1/√2)·100%. Доля же распавшихся ядер, очевидно, окажется равной (1-1/√2)·100% = 29%.
Правильный ответ: 4.
№ 4. Период полураспада — это время за которое распадается половина имеющихся радиоактивных ядер. Из графика видно, что наименьшим периодом полураспада обладает элемент Г.
Ответ: 4.
№ 5. Согласно закону радиоактивного распада, по истечении времени t от первоначальной массы радиоактивного изотопа m0 останется примерно
m = m0·2-t/T = 104 г ·2-5,2/2,6 = 26 г.
Правильный ответ: 2.
№ 6. Период полураспада - время, за которое число ядер данного изотопа уменьшается в два раза. Из графика видно, что период полураспада ядер эрбия 173Er68 равен 60 с.
Правильный ответ: 1.
Подготовка к ЕГЭ
Закон радиоактивного распада
Ответы
Задание № 4
№ 1. Согласно закону радиоактивного распада, по истечении времени t от первоначального количества атомов N0 радиоактивного вещества с периодом полураспада T останется примерно N=N0·2-t/T атомов. Следовательно, по истечении времени двух периодов полураспада останется N=N0·2-2T/T = N0/4 атомов, то есть 25%.
Правильный ответ: 1.
№ 2. Количество ядер меняется со временем по закону N=N0·2-t/T где N0 - количество атомов в начале наблюдения, t - время прошедшее от начала наблюдения и T - период полураспада. Рассчитаем количество ядер для каждого момента времени, отмеченного на графике:
N(5) = 8·1020·2-5/5 = 4·1020 ядер;
N(10) = 8·1020·2-10/5 = 2·1020 ядер;
N(15) = 8·1020·2-15/5 = 1020 ядер;
N(30) = 8·1020·2-30/5 = 1/8·1020 ядер.
Из рисунка видно, что график пройдёт через точку D.
Правильный ответ указан под номером: 4.
№ 3. Период полураспада - это время, в течение которого распадается половина наличного числа радиоактивных атомов. Верным является утверждение, что половина изначально имевшихся ядер франция распадется за 4,8 минуты.
Правильный ответ: 4.
№ 4. Период полураспада - это время, в течение которого распадается половина наличного числа радиоактивных атомов. Поскольку в образце, содержащем большое количество атомов тория 227Th90, через 19 суток останется половина начального количества атомов, заключаем, что период полураспада ядер атомов тория составляет 19 суток.
Привальный ответ: 4.
№ 5. Период полураспада — время, за которое число ядер данного изотопа уменьшается в два раза. Из графика видно, что период полураспада ядер радиоактивного изотопа равен 2 месяца.
Правильный ответ: 2.
№ 6. Согласно закону радиоактивного распада: N=N0·2-t/T. Таким образом, доля атомов, распавшихся по прошествии интервала времени, равного половине периода полураспада, равна (N0-N(T/2))/N0 = 1 – 2-(-T/2)/T = 0,3.
На гистограмме этому ответу соответствует столбец под номером 3.
Правильный ответ: 3.