Файл: Лабораторная работа 1 по теме Методы решения нелинейных уравнений.docx

Для метода золотого сечения теоретическая длина отрезка неопределенности после трех итераций равна 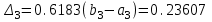, что совпадает с полученной длиной отрезка неопределенности.

8. 
   Число итераций, необходимых длялокализации точки минимума и Е=10^-4
   

Теоретическая величина погрешности для метода золотого сечения определяется длиной конечного отрезка неопределенности после Nитераций . Отсюда имеем , (L₂₀=0.000066034).

Длина отрезка равна 0.00011при расчете на ПК(N=19) . Точность достигнута при N=20. То есть, расчет совпадает с теоретической оценкой.

6.6. Контрольные вопросы по теме «Одномерная оптимизация»

1. 
   Какое значение функции называют оптимальным?
   
2. 
   В чем заключается задача одномерной оптимизации?
   
3. 
   Какой минимум называют локальным?
   
4. 
   Что такое глобальный минимум?
   
5. 
   Каковы необходимые и достаточные условия экстремума функции?
   
6. 
   Когда применяются численные методы одномерной оптимизации?
   
7. 
   В чем их преимущества и недостатки по сравнению с аналитическими методами?
   
8. 
   В чем суть методов одномерного поиска, и при каких условиях они применяются?
   
9. 
   Что означает понятие «унимодальная функция»?
   
10. 
    В чем суть условия унимодальности?
    
11. 
    Почему в методах одномерной оптимизации при переходе к следующей итерации часть отрезка можно отбросить?
    
12. 
    Какое деление отрезка называют «золотым сечением»?
    
13. 
    В чем суть метода дихотомии?
    
14. 
    В чем суть метода золотого сечения?
    
15. 
    Влияет ли вид функции на скорость сходимости метода дихотомии?
    
16. 
    Влияет ли вид функции на скорость сходимости метода золотого сечения?
    
17. 
    В чем заключается основное достоинство метода золотого сечения?
    
18. 
    Во сколько раз на очередной итерации уменьшается длина отрезка неопределенности в методе дихотомии?
    
19. 
    Во сколько раз на очередной итерации уменьшается длина отрезка неопределенности в методе золотого сечения?
    
20. 
    Как оценивается погрешность методов оптимизации?
    
21. 
    Можно ли найти максимум функции, используя численные методы одномерной оптимизации?
    

---

---