Файл: Лабораторная работа 1 по теме Методы решения нелинейных уравнений.docx

1.5. Содержание отчета

1. Фамилия и имя студента, номер группы.

2. Название и цель лабораторной работы.

3. Индивидуальный вариант задания к работе.

4. Таблицы 1–3 с перенумерованными узлами интерполяции.

5. Интерполяционные формулы для ручных расчетов и результаты расчетов в таблицах 1–4 и 1-5.

6. Выводы.

1.6. Пример выполнения задания

1. 
   Точка интерполяции для формулы Лагранжа b = 0.52.
   

Выбор и перенумерация узлов.

Для ручной интерполяции в точке x = b = 0.52 по формуле Лагранжа выбираем из таблицы 3–2 4 узла так, чтобы точка b = 0.52 оказалась внутри получающийся таблицы и узлы были наиболее близкими к этой точке. В итоге выбираем узлы с номерами 8, 9, 10, 11:

8	0.45	-3.4890
9	0.50	-3.3250
10	0.55	-3.1385
11	0.60	-2.9280

Следует отметить, что формула Лагранжа может использоваться как для таблиц с постоянным шагом, так и с непостоянным шагом. Перенумеруем узлы интерполяции руководствуясь двумя правилами: точка x=b должна быть внутри таблицы и узлы должны быть ближайшие к ней. Занесем перенумерованные узлы в таблицу вида 2–3:

k	0	1	2	3
xk	0.50	0.55	0.45	0.60
yk	-3.3250	-3.1385	-3.4890	-2.9280

Ручной расчет по формуле Лагранжа.

Запишем интерполяционные полиномы Лагранжа 1–й, 2–й и 3–й степени и вычислим их значения в точке

---

x = b = 0.52:





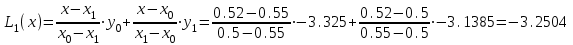
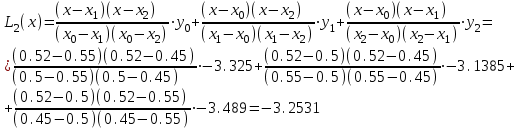
Обратите внимание, что: выражения для полиномов 1, 2 и 3 степени (в явном виде) после соответствующих преобразований следует получить самостоятельно!

Занесем результаты в таблицу и вычислим оценки погрешности полученных значений для многочленов 1–й и 2–й степени:

Степень многочлена k	Lk(x)	Оценка погрешности
1	–3.2504	0.0027
2	–3.2531	0.0001
3	–3.2532	–

Вывод. Получены выражения для интерполяционных полиномов 1, 2 и 3-ей степени и их значения в т. b. Оценку погрешности проведём в соответствии с неравенством:


Можно утверждать, что разность между точным (неизвестным) значением функции и значением интерполяционного полинома в точке x=0.52 после 3=х итераций не превышает 0.0001.

1. 
   Точка интерполяции для формулы Ньютона a = 0.12.
   

Выбор и нумерация узлов.

Для ручной интерполяции в точке x = a = 0.12 по 1 формуле Ньютона выбираем 4 узла из таблицы 1–2 так, чтобы точка a = 0.12 оказалась между узлами с номерами с 1 по 2 и добавляем узлы вправо:

Номера выбранных узлов (k)	xk	yk
1	0.10	-4.1330
2	0.15	-4.0845
3	0.20	-4.0240
4	0.25	-3.9500

---

Выбор точек определяется тем, чтобы при решении задачи интерполяции в точке по первой формуле Ньютона, точка должна быть внутри таблицы для полинома любой степени, в том числе и первой. Поэтому нулевой и первый узел должны находиться по разные стороны от самой точки x=a. Если нулевой узел находится слева от точки, а первый узел находится справа от точки, то шаг h=x1-x0 будетположительным и добавлять узлы следует справа относительно точки x=a. Если же нулевой узел находиться справа от точки, а первый узел находиться слева, то шаг h=x1-x0 будет отрицательным, и добавлять узлы следует слева.

Изменим нумерацию узлом интерполяции для использования их в интерполяционных формулах и занесем в таблицы вида 1–3.

k	0	1	2	3
xk	0.10	0.15	0.20	0.25
yk	-4.1330	-4.0845	-4.0240	-3.9500

Ручной расчет по формуле Ньютона.
Заполним таблицу конечных разностей:

x	y	Δy	Δ2y	Δ3y
0.10	-4.1330	0.0485	0.0120	0.0015
0.15	-4.0845	0.0605	0.0135
0.20	-4.0240	0.0740
0.25	-3.9500

---

Запишем 1–ю интерполяционную формулу Ньютона



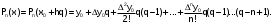
для полиномов 1–й, 2–й и 3–й степени и выполним расчеты по ним. Определим значение q:



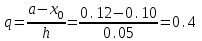
Значение полинома 1-й степени в т. x=0.12:


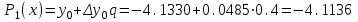
Значение полинома 2-й степени в т. x=0.12:



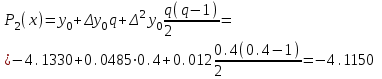
Значение полинома 3-й степени в т. x=0.12:
Важно: Явные выражения для полиномов 1, 2 и 3 степени могут быть получены после соответствующих преобразований формулы:


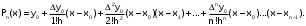
В нашем случае они будут иметь вид:


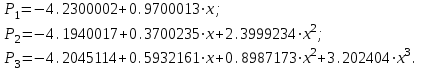
Занесем результаты в таблицу и вычислим оценки погрешности полученных значений для полиномов 1–й и 2–й степени:

Степень многочлена k	Pk(x)	Оценка погрешности
1	–4.1136	0.0014
2	–4.1150	0.0001
3	–4.1149	–

Вывод. Получены выражения для интерполяционных многочленов 1, 2 и 3-ей степени и их значения в точке а. Оценку погрешности проведём в соответствии с неравенством:



Можно утверждать, что разность между точным (неизвестным) значением функции и значением интерполяционного полинома в точке x=0.12 после 3-х итераций не превышает 0.0001.

Контрольные вопросы по теме

«Интерполяция функций»

1. 
   Что называется задачей интерполяции и задачей аппроксимации?
   
2. 
   Что называется узлами и шагом интерполяции?
   
3. 
   Что такое интерполируемая функция и интерполирующая функция?
   
4. 
   Существует ли связь между числом узлов интерполяции и степенью интерполяционного многочлена?
   
5. 
   Можно ли, используя одни и те же узлы интерполяции, построить несколько интерполяционных полиномов?
   
6. 
   Сколько интерполяционных полиномов степени n существует, если функция задана (n + 1) узлом?
   
7. 
   Изменится ли точность интерполяции при увеличении или уменьшении количества узлов?
   
8. 
   Как изменится формула Лагранжа при добавлении в таблицу значений функции еще одного узла?
   
9. 
   Как изменится формула Ньютона при добавлении в таблицу значений функции еще одного узла?
   
10. 
    Если интерполируемая функция f(x)задана в (n + 1) равноотстоящих узлах, то для ее интерполяции удобнее использовать формулу Ньютона или формулу Лагранжа?
    
11. 
    Можно ли при использовании формулы Лагранжа располагать узлы интерполяции в произвольном порядке?
    
12. 
    Можно ли при использовании формулы Ньютона располагать узлы интерполяции в произвольном порядке?
    
13. 
    Потребуется ли полный пересчет коэффициентов формулы Лагранжа при добавлении дополнительного узла интерполяции?
    
14. 
    В чем заключается универсальность формулы Лагранжа?
    
15. 
    От чего зависит точность интерполяции?
    
16. 
    Что такое «конечные разности»?
    
17. 
    Чему равен порядок конечной разности наивысшего порядка, полученный по n исходным точкам?
    
18. 
    Что происходит с формулой Ньютона при добавлении очередного узла интерполяции?
    
19. 
    Чем отличаются результаты интерполяции, если при построении интерполяционных полиномов по формулам Лагранжа и Ньютона были использованы одни и те же узлы?
    
20. 
    Чему равна степень интерполяционного полинома Ньютона при трех заданных точках интерполируемой функции?
    

---

---