Файл: Лабораторная работа 1 по теме Методы решения нелинейных уравнений.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 132
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лабораторная работа по теме 3.
«Аппроксимация функций.
Метод наименьших квадратов»
2.1. Вопросы, подлежащие изучению
-
Постановка задачи аппроксимации. -
Основные понятия: базисные функции, матрица Грамма, система нормальных уравнений, критерий аппроксимации. -
Матрица Грамма для степенного базиса. -
Правило построения системы нормальных уравнений и число уравнений в системе. -
Алгоритм получения коэффициентов линейных и квадратичных аппроксимирующих функций. -
Графическая иллюстрация метода МНК. -
Формулы оценки качества аппроксимации.
3.2. Задание
-
Выбрать индивидуальное задание из табл. 3-1 и табл. 3-2 для решения задачи аппроксимации методом наименьших квадратов: значения функции табл. 2-2 в узлах, указанных в табл. 2-1. -
Выполнить линейную аппроксимацию:
-
составить систему нормальных уравнений и решить её;
-
вычислить значения аппроксимирующих функций в узловых точках и сравнить их со значениями исходной функции;
-
Вычислить среднеквадратичную погрешность (СКО).
-
С использованием математического пакета получить аппрокси-мирующие полиномы МНК 1, 2, 3, 4, 5 степеней и соответствующие СКО. Построить графики полученных полиномов. -
Проанализировать результаты.
3.3. Варианты задания
Таблица 3-1
| N варианта | Функция из табл. 3-2 | Номера узлов из табл. 3-2 |
| 1 | 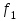 | 1,35,7,9,11,13 |
| 2 | 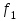 | 2,4,6,8,10,12,14 |
| 3 | 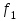 | 4,6,8,10,12,14 |
| 4 | 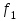 | 5,7,9,11,13,15 |
| 5 | 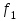 | 7,8,9,10,11,12,13 |
| 6 | 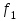 | 3,5,7,9,11,13,15 |
| 7 | 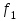 | 9,11,13,15,17,19 |
| 8 | 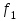 | 10,12,14,16,18,20 |
| 9 | 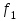 | 15,17,19,21,23,25 |
| 10 | 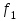 | 16,18,20,22,24,26 |
| 11 | 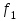 | 17,19,21,23,25,27 |
| 12 | 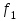 | 21,23,25,27,29,31 |
| 13 | 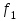 | 22,24,26,28,30,32 |
| 14 | 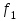 | 27,29,31,33,35 |
| 15 | 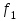 | 28,29,30,31,32,33 |
| 16 | 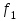 | 28,30,32,34,36 |
| 17 | 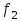 | 1,3,5,7,9,11 |
| 18 | 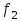 | 2,4,6,8,10,12 |
| 19 | 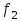 | 3,5,7,9,11,13 |
| 20 | 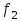 | 4,6,8,10,12,14 |
| 21 | 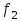 | 5,7,9,11,13,15 |
| 22 | 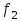 | 10,12,14,16,18,20 |
| 23 | 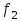 | 11,12,13,14,15,16,17 |
| 24 | 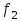 | 15,17,19,21,23,25 |
| 25 | 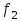 | 16,18,20,22,24,26 |
| 26 | 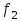 | 19,21,23,25,27,29 |
| 27 | 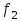 | 21,23,25,27,29,31 |
| 28 | 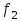 | 24,25,26,27,28,29,30 |
| 29 | 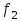 | 26,28,30,32,34,36 |
| 30 | 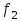 | 25,27,29,31,33,35 |
Таблица 3-2
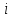 -номер узла -номер узла | 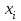 | 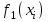 | 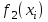 |
| 1 | -1.5 | -1,15 | 1,25 |
| 2 | -1.4 | -0,506 | 1,594 |
| 3 | -1.3 | 0,236 | 2,056 |
| 4 | -1.2 | 0,88 | 2,44 |
| 5 | -1.1 | 1,256 | 2,577 |
| 6 | -1.0 | 1,266 | 2,366 |
| 7 | -0.9 | 0,91 | 1,81 |
| 8 | -0.8 | 0,286 | 1,006 |
| 9 | -0.7 | -0,436 | 0,124 |
| 10 | -0.6 | -1,06 | -0,64 |
| 11 | -0.5 | -1,416 | -1,116 |
| 12 | -0.4 | -1,406 | -1,206 |
| 13 | -0.3 | -1,03 | -0,91 |
| 14 | -0.2 | -0,386 | -0,326 |
| 15 | -0.1 | -0,356 | 0,376 |
| 16 | 0.0 | 1 | 1 |
| 17 | 0.1 | 1,376 | 1,376 |
| 18 | 0.2 | 1,386 | 1,406 |
| 19 | 0.3 | 1,03 | 1,09 |
| 20 | 0.4 | 0,406 | 0,526 |
| 21 | 0.5 | -0,316 | -0,116 |
| 22 | 0.6 | -0,939 | -0,64 |
| 23 | 0.7 | -1,296 | -0,876 |
| 24 | 0.8 | -1,286 | -0,726 |
| 25 | 0.9 | -0,91 | -0,19 |
| 26 | 1.0 | -0,266 | 0,634 |
| 27 | 1.1 | 0,476 | 1,576 |
| 28 | 1.2 | 1,12 | 2,44 |
| 29 | 1.3 | 1,496 | 3,056 |
| 30 | 1.4 | 1,506 | 3,326 |
| 31 | 1.5 | 1,15 | 3,25 |
| 32 | 1.6 | 0,526 | 2,926 |
| 33 | 1.7 | -0,196 | 2,524 |
| 34 | 1.8 | -0,82 | 2,24 |
| 35 | 1.9 | -1,176 | 2,244 |
| 36 | 2.0 | -1,66 | 2,634 |
3.4. Содержание отчета
-
Индивидуальное задание. -
Линейная аппроксимация:
-
значения элементов матрицы Грамма и столбцов свободных членов, представленные в табл. 3-3:
Таблица 3-3
 |  | 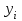 | 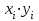 | 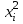 |
| 0 | | | | |
| 1 | | | | |
| 2 | | | | |
| 3 | | | | |
| 4 | | | | |
| 5 | | | | |
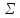 | | | | |
-
системы нормальных уравнений и их решения, аппроксимирующие функции; -
исходная функция и результаты аппроксимации в узловых точках, представленные в табл. 3-4:
в узловых точках, представленные в табл. 3-4:
Таблица 3-4
 | | | | | |
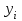 | | | | | |
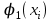 | | | | | |
 | | | | | |
-
оценка погрешности (среднеквадратическое отклонение).
-
Аппроксимация с помощью математического пакета.
3.5. Пример выполнения задания
-
Задание для решения задачи аппроксимации
Для решения задачи аппроксимации методом наименьших квадратов выберем функцию y(x), заданную следующей таблицей:
 | 1.0 | 1.2 | 1.4 | 1.6 | 1.8 | 2.0 |
 | 0.634 | 2.44 | 3.326 | 2.926 | 2.24 | 2.634 |
-
Линейная аппроксимация:
Вычислить и записать в табл. 3-3 элементы матрицы Грамма и столбец свободных членов:
 |  |  |  |  |
| 0 | 1.0 | 0.634 | 0.634 | 1 |
| 1 | 1.2 | 2.44 | 2.928 | 1.44 |
| 2 | 1.4 | 3.326 | 4.6564 | 1.96 |
| 3 | 1.6 | 2.926 | 4.6816 | 2.56 |
| 4 | 1.8 | 2.24 | 4.032 | 3.24 |
| 5 | 2.0 | 2.634 | 5.268 | 4 |
 | 9 | 14.2 | 22.2 | 10.2 |