Файл: Лабораторная работа 1 по теме Методы решения нелинейных уравнений.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 122
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Содержание отчета
-
Индивидуальное задание. -
Результаты исследования индивидуального варианта задания:
-
график функции ;
; -
начальный отрезок неопределенности; -
результаты проверки аналитического условия унимодальности функции на отрезке.
-
Результаты расчета трех итераций ручным методом представить в табл. 6-2.
Таблица 6-2
| № итерации | a | b | x1 | x2 | f(x1) | f(x2) | |
| 1 | | | | | | | |
| 2 | | | | | | | |
| 3 | | | | | | | |
-
Программа, реализующая заданный метод с точностью 10-4. -
Число итераций, необходимые для локализации точки минимума используемыми методами.
-
Пример выполнения контрольного задания
-
Задание для решения задачи одномерной оптимизации:
-
функция, для которой необходимо найти минимум – ;
;
-
Исследование задания:
-
график функции , построенный на достаточно большом отрезке ОДЗ функции:
, построенный на достаточно большом отрезке ОДЗ функции:
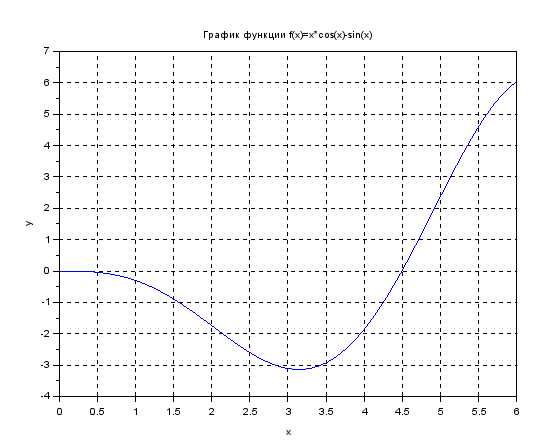
-
выберем по построенному графику функции начальный отрезок неопределенности (отрезок, содержащий точку минимума): отрезок [2.5;3.5]; -
проверим выполнение аналитического условия унимодальности функции на выбранном отрезке:
обращаются в нуль одновременно и
Значения
| х | 2.5 | 2.6 | 2.7 | 2.8 | 2.9 | 3.0 | 3.1 | 3.2 | 3.3 | 3.4 | 3.5 |
| f’(x) | -1.44 | -1.34 | -1.15 | -0.94 | -0.69 | -0.42 | -0.13 | 0.19 | 0.52 | 0.87 | 1.23 |
На отрезке [2.5;3.5] функция
Метод дихотомии
5. Результаты выполнения функции, реализующей метод золотого сечения и длина отрезка, содержащего точку минимума после трех итераций. Значение параметра d метода дихотомии выберем равным 0.01.
Для проведения расчетов по методу дихотомии следует создать сценарий и выполнить расчеты 3-х итераций. Ниже приведен пример 1-й итерации:
1).

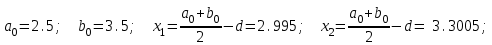
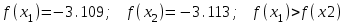
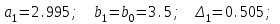
Вычислить аналогично следующие 2 итерации, а результаты расчетов свести в табл. 6.3:
| n | a | b | х1 | х2 | f(x1) | f(x2) | |
| 1 | 2.5 | 3.5 | 2.995 | 3.005 | -3.109 | -3.113 | 0.505 |
| 2 | 2.995 | 3.5 | 3.2425 | 3.2525 | -3.125 | -3.122 | 0.2575 |
| 3 | 2.995 | 3.2525 | 3.119 | 3.129 | -3.1407 | -3.141 | 0.134 |
| 4 | 3.119 | 3.2525 | | | | | |
Для метода дихотомии длина отрезка неопределенности после трех итераций равна
-
Число итераций, необходимых для локализации точки минимума и Е=10-4
Теоретическая величина погрешности для метода дихотомии определяется длиной конечного отрезка неопределенности после N итераций:
Если точностьЕ=0.0001, а параметр метода d=
В результате расчета на ПК при N=13 длина отрезка равна 0.00014. Точность достигнута при N=14,т. е. расчет совпадает с теоретической оценкой.
Метод золотого сечения
-
Результаты выполнения функции, реализующей метод золотого сечения и длина отрезка, содержащего точку минимума после трех итераций
Для проведения расчетов по методу золотого сечения следует создать сценарий и выполнить расчеты 3-х итераций. Ниже приведен пример 1-й итерации:
1).
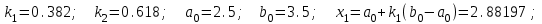
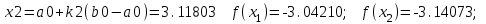
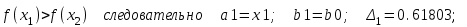
Вычислить аналогично следующие 2 итерации, а результаты расчетов свести в таблицу 6.4:
Таблица 6-4
| N | a | b | x1 | x2 | f(x1) | f(x2) | |
| 0 | 2.5 | 3.5 | 2.88197 | 3.11803 | -3.04210 | -3.14073 | 0.61803 |
| 1 | 2.88197 | 3.5 | 3.11803 | 3.26393 | -3.14073 | -3.11750 | 0.38197 |
| 2 | 2.88197 | 3.26393 | 3.02786 | 3.11803 | -3.12179 | -3.14073 | 0.23607 |
| 3 | 3.02786 | 3.26393 | | | | | |