Файл: Статистический анализ экспорта лесных ресурсов рф за период 20082009 гг.rtf
Добавлен: 04.12.2023
Просмотров: 70
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
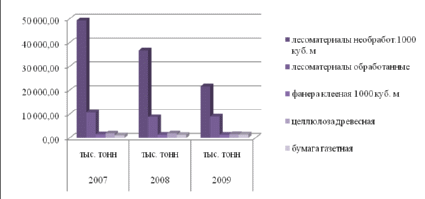
График 1. Динамика экспорта лесных ресурсов.
Основная цель статистического изучения динамики экспортных операций состоит в выявлении и измерении закономерностей их развития во времени. Это достигается посредством построения и анализа статистических рядов динамики.
Рядами динамики называются статистические данные, отображающие развитие изучаемого явления во времени. В каждом ряду динамики имеются два основных элемента: показатель времени t; соответствующие им уровни развития изучаемого явления у. В качестве показаний времени в рядах динамики выступают либо определенные даты (моменты) времени, либо отдельные периоды (годы, кварталы, месяцы, сутки).
Уровни рядов динамики отображают количественную оценку (меру) развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными или средними величинами.
В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определенным датам (моментам) времени, или к отдельным периодам. В соответствии с этим, ряды динамики подразделяются на моментные и интервальные.
В нашем случае, рассматриваемые ряды динамики относятся к интервальным, так как они отображают итоги развития (функционирования) изучаемых явлений за отдельные периоды времени (2007-2009 г.). Особенностью интервального ряда динамики является то, что каждый его уровень складывается из данных за более короткие интервалы времени.
Ряды динамики могут быть полными и неполными. Наш рассматриваемый ряд - полный, то есть одноименные моменты времени или периоды времени строго следуют один за другим в календарном порядке или равноотстоят друг от друга.
Ряды динамики, изучающие изменение статистического показателя, могут охватывать значительный период времени, на протяжении которого могут происходить события, нарушающие сопоставимость отдельных уровней ряда динамики (изменение методологии учета, изменение цен и т.д.).
.2.1 Определение среднего уровня ряда динамики
В качестве обобщенной характеристики уровней ряда динамики служит средний уровень ряда динамики
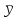. В зависимости от типа ряда динамики используются различные расчетные формулы.
Рассчитается средний уровень для интервального ряда абсолютных величин с равными периодами времени по формуле:
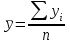, где 
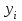- уровни ряда, сохраняющиеся без изменения на протяжении интервала времени, n - количество уровней ряда.Табл.3 Динамика экспорта продукции лесной промышленности
| Наименование товара | 2007 | 2008 | 2009 | ỹ |
| | тыс. тонн | тыс. тонн | тыс. тонн | тыс. тонн |
| лесоматериалы необработ.1000 м3 | 49333,1 | 36739,2 | 21652,7 | 35908,33 |
| лесоматериалы обработанные | 10705,2 | 8810,9 | 9060 | 9525,367 |
| фанера клееная 1000 м3 | 1493 | 1332,4 | 1325,2 | 1383,533 |
| целлюлоза древесная | 1891,4 | 1905,2 | 1570,3 | 1788,967 |
| бумага газетная | 1108,9 | 1292,8 | 1420,5 | 1274,067 |
.2.2 Расчет показателей изменения уровней ряда динамики
Одним из важнейших направлений анализа рядов динамики является изучение особенностей развития явления за отдельные периоды времени.
С этой целью для динамических рядов рассчитывают ряд показателей:
ᶄ- коэффициент роста;
К - темпы роста;
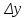- абсолютные приросты;
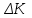- темпы прироста.Коэффициент роста - отношение показателя, какого либо явления изучаемого периода к показателю базисного периода, что можно представить в виде формулы ᶄ=
, где
yi - величина изучаемого явления, y0 - величина явления базисного периода.
Табл.4 Коэффициенты роста экспорта продукции лесной промышленности.
| Наименование товара | 2007 | 2008 | 2009 |
| лесоматериалы необработ.1000 м3 | - | 0,7447 | 0,4389 |
| лесоматериалы обработанные | - | 0,8230 | 0,8463 |
| фанера клееная 1000 м3 | - | 0,8924 | 0,8876 |
| целлюлоза древесная | - | 1,0073 | 0,8302 |
| бумага газетная | - | 1,1658 | 1,2810 |
Темп роста - относительный показатель, получающийся в результате деления двух уровней одного ряда друг на друга. Темпы роста могут рассчитываться как цепные, когда каждый уровень ряда сопоставляется с предшествующим ему уровнем, либо как базисные, когда все уровни ряда сопоставляются с одним и тем же уровнем
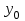, выбранным за базу сравнения.Сначала производятся расчёты цепного темпа роста, по формуле
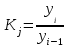. Для вычисления темпа роста за 2007 год, потребуются данные экспортных операций за 2006 год.Табл.5 Темп роста (цепной) экспорта продукции лесной промышленности.
| Наименование товара | 2007 | 2008 | 2009 |
| лесоматериалы необработ.1000 м3 | 96,5644 | 74,4717 | 58,9362 |
| лесоматериалы обработанные | 109,8927 | 82,3049 | 102,8272 |
| фанера клееная 1000 м3 | 95,0955 | 89,2431 | 99,4596 |
| целлюлоза древесная | 99,7732 | 100,72962 | 82,4218 |
| бумага газетная | 88,1128 | 116,5840 | 109,8778 |
Темп роста базисный рассчитывается по формуле
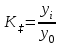. За базисный уровень взяты данные экспорта лесных товаров за 2007 год.Табл.6 Темп роста (базисный) экспорта продукции лесной промышленности.
| Наименование товара | 2007 | 2008 | 2009 |
| лесоматериалы необработ.1000 м3 | - | 74,4717 | 43,8908 |
| лесоматериалы обработанные | - | 82,3048 | 84,6318 |
| фанера клееная 1000 м3 | - | 89,2431 | 88,7609 |
| целлюлоза древесная | - | 100,7296 | 83,0232 |
| бумага газетная | - | 116,5840 | 75,1031 |
Абсолютный прирост - разность между двумя уровнями ряда динамики, имеет ту же размерность, что и уровни самого ряда динамики. Абсолютные приросты могут быть цепными и базисными.
Сначала рассчитываются значения абсолютного прироста цепного по формуле
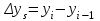, где 
- рассматриваемый уровень ряда, а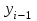 
- предшествующийТабл.7 Абсолютный прирост (цепной) экспорта продукции лесной промышленности.
| Наименование товара | 2007 тыс. тонн | 2008 тыс. тонн | 2009 тыс. тонн |
| лесоматериалы необработ.1000 м3 | -1755,2 | -12593,9 | -15086,5 |
| лесоматериалы обработанные | 963,7 | -1894,3 | 249,1 |
| фанера клееная 1000 м3 | -77 | -160,6 | -7,2 |
| целлюлоза древесная | -4,3 | 13,8 | -334,9 |
| бумага газетная | -149,6 | 183,9 | 127,7 |