Анықтама: Х жиыны х₁х₂...,.х_n кластарына бөлінді деп есептеледі, егер 1) х₁х₂...,.х_n ішкі жиындары қос-қостан қиылыспаса;

2) х₁х₂...,.х_n ішкі жиындарының бірігуі X жиынына тең болса.

Егер осы екі шарттың біреуі орындалмаса, онда классификациялау дұрыс емес деп есептеледі.

Пайдаланылған әдебиеттер тізімі

1. О.М.Жолымбаев. Математика : Студенттерге арналған оқу құралы. –Алматы: 2004. -384 б.

2. Стойлова Л.П.. Математика. Учебное пособие для студентов педвузов, -

М.,2004

3. Т.Қ.Оспанов. Математика. –А.: 2000ж.

4. О.М.Жолымбаев, Г.Е.Берікханова. Математика: Алматы: 2004ж.

5. К.С.Алиева. Математика: Оқу құралы. :Шымкент. 2000ж.

6. Л.П.Стойлова. Математика. М.: 2004ж.

Бақылау сұрақтары

1. 
   Жиын дегеніміз не?
   
2. 
   Жиынға қатысты қолданылатын ұғымдарды ата.
   
3. 
   Жиындар қалай бері леді?
   
4. 
   Эйлер-Венн диаграммасы дегеніміз не?
   
5. 
   Жиындарға қандай амалдар қолданылады?
   
6. 
   Жиындарға қатысты заңдарды ата.
   

Лекция 2

Тақырыбы: Графтар
Жоспар

1. 
   Жиындардың декарттық көбейтіндісі.
   
2. 
   Граф ұғымы.
   

1. Егер жиындағы элементтердің орналасу реті ескерілетін болса, математикада элементтердің реттелген жиынтығы берілген деп айтады. Берілген тапсырмада реттелген қостармен кездестік.

а және b элементтерінен құрылған реттелген қостарды (а, b) түрінде белгілейді де, а -ны қостың бірінші координаты (компоненті), b-ны екінші координаты (компоненті) деп атайды. Егер a = с мен b = d; шарты орындалса, (а, b) және (с. d) қостары тең деп аталады.

Реттелген костарды әртүрлі екі жиынның элементтерінен де құруға болады. Мысалы, А = {1;2;3} және В = {3;5) жиындарынан бірінші компоненті А жиьшынан, екінші компоненті В жиынынан алынатындай етіп реттелген қостар құру керек. Сонда мынандай жиын аламыз

{(1,3). (1,5), (2,3). (2,5), (3,3). (3.5) }

Бұл тапсырманы орындау барысында элементтері реттелген қостар болатын жаңа жиын алынды. Осы жиынды А және В жиыңдарының декарттық көбейтіндісі деп атайды.

---

А н ы қ т а м а: А және В жиындарының декарлық көбейтіндісі деп бірінші компоненті А жиынынан, екінші компоненті В жиынынан алынған барлық реттелген қостардың жиынын айтады.

А және В жиындарының декарттық көбейтіндісі былай белгіленеді: АхВ. Декарттық көбейтіндіні табатын амалды жиындарды декарттык, көбейту деп атайды.

Жиындарды декарттық көбейту ауыстырымдылық заңына бағынбайды, яғни АхВ≠ВхА болатындай А және В жиындары бар болады. Жоғарыдағы мысалдағы A, B жиындарының АхВ және ВхА жиынын құрайық.

АхВ = {(13), (1,5), (2,3), (2,5), (3,3), (3,5) }

ВхА = {(3,1), (3,2), (3,3), (5,1), (5,2), (5,3) }

Бұдан АхВ және ВхА жиындарының әртүрлі элементтерден тұратынын көреміз, яғни АхВ ≠ ВхА.

Жиындарды декарттық көбейту амалы терімділік заңына да бағынбайды, бірақ бірігу амалына қатысты декарттық көбейту үлестірімді болады: А, В және С жиындары үшін (АUВ)хС = (АхС)U(ВхС) теңдігі тура болады.

Екі ақырлы жиынның декарттық көбейтіндісін кесте арқылы жазу ыңғайлы.

Математикада реттелген қостар ғана емес, реттелген үштік, терттік т.с.с. элементтер жиынтығы да қарастырылады. Мұндай реттелген жиынтықтар кортеждер деп аталады. Кортеждегі элементтің саны оның ұзындығын анықтайды. Кортеж ұғымын пайдаланып п жиынның декарттық көбейтіндісін анықтауға болады.

Анықтама: А₁, А₂,... А_n, жиындарынын декарттық көбейтіндісі деп бірінші компоненті А₁-ден, екінші компоненті А₂-ден, т.с.с. п-ші компоненті джиынынан алынған, ұзындығы п-ге тең кортеждердің жиынын айтады.

Оны А₁, А₂,... А_n түрінде белгілейді.

А₁ = {2,3}, А₂ = {3, 4, 5}, А₃ {7, 8} болсын.

А₁ х А₂ х А₃ көбейтіндісін табу керек.

А₁ х А₂ х А₃ = {(2,3,7),(2,3,8),(2,4,7),(2,4,8),(2,5,7),(2,5.8),(3,3,7),(3,

3,8),(3,4,7),(3,4,8),(3,5,7),(3,5,8):

Егер А 3-тен артық натурал сандар жиыны, В 5-тен артық натурал сандар жиыны болса, олардың декарттық көбейтіндісін қалай көрсетуге болады?

---

2. Эйлер дөңгелектерін бұл жағдайда пайдалану өте қолайсыз. Математикада бұл мәселені координаттық жазықтықтар арқылы шешеді.

Координаттық түзу деп санақ басы, бірлік кесінді және оң бағыты көрсетілген түзуді айтады. (1-сызба).



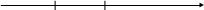
О Е L

1- сызба

Координаттық түзудің міндеті қандай?

l түзуінің бойынан М нүктесін (М нүктесі О мен беттеспейді) алып, оған х санын сәйкес қоямыз, сонда:

1) оның модулі О-дан М-ге дейінгі қашықтыққа тең;

2) егер М нүктесі ОЕ сәулесінде жатса, х саны оң, ал М қарама-қарсы

сәуледе жатса х саны теріс болады. Осылай анықталған х саны М нүктесінің координатасы деп аталып м(х) түрінде белгіленеді.

Ох түзуін абсцисса осі, ал Оу түзуін ордината осі деп атау келісілген. Тік бұрышты координаттар жүйесі орналасқан жазықтықты координаттық жазықтық деп атайды.

Координаттық жазықтыктың міндеті кандай?

Координаттық жазықтықтан М нүктесін алайық (16-сызба). Оның орны абсцисса және ордината деп аталатын екі санмен анықталады. М нүктесінің абсциссасы - оның Ох осіндегі проекциясы М₁ нүктесінің координатасы х, ал ординатасы - Оу осіндегі проекциясы М₂ нүктесінің координатасы у болады. Сонда М нүктссінің абсциссасы х, ординатасы у дегенді М(х,у) түрінде жазады.

Сонымен, тік бұрышты координаттар жүйесі жазықтықтағы әрбір нүктеге оның координаталары болатын нақты сандардың бір ғана қосын сәйкес қояды, және керісінше, нақты сандардың әрбір (х,у) қосына жазықтықтан бір ғана нүкте сәйкес келеді.

Түзудегі және жазықтықтағы нүктенің координатасы ұғымын XVII ғасырда француз ғалымы және философы Рене Декарт геометрияға енгізді. Бұл оқиға математикада жаңа дәуірдің - функция ұғымы мен геометриялық түрлендірулердің пайда болу және даму дәуірі болды.

Рене Декарттың атыммен жазықтықтағы тік бұрышты координаталар жүйесі декарттық координаттар жүйесі деп те аталады.

А және В сандық жиындар болсын. Сонда осы жиындардың декарттық көбейтіндісі сандардың реттелген қостарының жиыны болады. Әрбір қосты жазықтықтағы нүктемен белгілесек, А және В жиындарының декарттық көбейтіндісін бейнелейтін фигураны аламыз.

---

Пайдаланылған әдебиеттер тізімі

1. О.М.Жолымбаев. Математика : Студенттерге арналған оқу құралы. –Алматы: 2004. -384 б.

2. Стойлова Л.П.. Математика. Учебное пособие для студентов педвузов, -

М.,2004

3. Т.Қ.Оспанов. Математика. –А.: 2000ж.

4. О.М.Жолымбаев, Г.Е.Берікханова. Математика: Алматы: 2004ж.

5. К.С.Алиева. Математика: Оқу құралы. :Шымкент. 2000ж.

6. Л.П.Стойлова. Математика. М.: 2004ж.

Бақылау сұрақтары

1. 
   Декарттық көбейтіндіні қалай есептейді?
   
2. 
   Граф ұғымы қалай енгізіледі?.
   
3. 
   Граф дегеніміз не?
   
4. 
   Қандай графты жазық граф дейміз?
   
5. 
   Эйлер теоремасын тұжырымда.
   

Лекция 3

Тақырыбы: Сәйкестіктер.

Жоспар

1. 
   Сәйкестік ұғымы. Кері сәйкестік. Олардың графы мен графигі.
   
2. 
   Бағдарланған графтар.
   
3. 
   Қатынастар.
   
4. 
   Қатынастың берілу тәсілдері.
   

1. Екі жиынның элементтерінің арасындағы қандай да бір байланыс жиі қарастырылады. Осындай байланысты сәйкестік деп атайды. Мысалы, кесінділердің ұзындығын өлшегенде кесінді мен нақты сандардың арасында, жазықтықтағы нүктелер мен нақты сандар қосының арасында сәйкестік бар.

Анықтама: Х және У жиындарының элементтерінің арасындағы сәйкестік деп олардың декарттық көбейтіндісінің ішкі жиыны болатын қостардың жиының айтады.

Ақырлы жиындардың арасындағы сәйкестік график арқылы көрнекті түрде бейнелеуге болады. Мысалы, Х = {3, 5, 7, 9}, У = {4, 6} жиындарының арасындағы «артық» (үлкен) деген сәйкестік график арқылы көрсетейік. Ол үшін берілген жиындардың элементтерін нүктелер арқылы кескіндеп, Х жиынының элементін кескіндейтін нүктеден У жиынының элементін кескіндейтін нүктені стрелкамен қосамыз, сонда элементтердің арасындағы «артық» сәйкестігі орындалуы керек. 5 > 4 болғандықтан стрелка 5 – тен 4 - ке қарай; 7 > 4, 7 > 6 болғандықтан 7 – ден 4 – ке, 7 – ден 6 – ға қарай т.с.с. бағытталуы тиіс. (1-сызба).


•4

•6

3•
5•


7•
9•

---

(1-сызба).

Сонда шыққан сызба Х және У жиындарының элементтерінің арасындағы «артық» деген сәйкестіктің графы болады.

Х, У сандық жиындардың арасындағы сәйкестікті координаттық жазықтықтағы график арқылы да көруге болады. Ол үшін қандай да бір R сәйкестікте болатын сандардың қосын координаттық жазықтықтағы нүктелер арқылы бейнелейді. Сонда алынған фигура R сәйкестігінің графигі болады.

Жоғарыда қарастырылған мысалдағы «артық» сәйкестігінің графигін сызайық. Берілген сәйкестікте болатын сандардың қосын жазайық: (5,4), (7,4), (7,6), (9,4), (9,6). Х жиынының элементтерін Ох осінің бойынан, У жиынының элементтерін Оу осінің бойынан алып, көрсетілген сандардың қосына сәйкес келетін нүктелерді координаттық жазықтықта белгілесек, Х және У жиындарының элементтерінің арасындағы «артық» сәйкестігінің графигін аламыз (2 - сызба).

У

6 ● ●



4 ● ● ●




0 1 3 5 7 9 х

(2 - сызба)

Енді «артық» сәйкестігін Х = R және У = {4, 6} жиындарында қарастырып, оның гафигін салайық. Бұл жағдайда Х жиынының элементтері бүкіл Ох осінің бойындағы нүктелерден, ал У жиыны екі элементтен тұрады. Х және У жиындарының элементтері үшін «артық» сәйкестігі берілгендіктен, Х жиынындағы 4 – тен артық болатын сандарды Ох осінің бойындағы 4 санына сәйкес келетін нүктенің оң жағында орналасқан. Демек, абсциссасы (4; ∞) аралығынан алынған, ал ординатасы 4 – ке тең болатын АВ сәулесі 4 – тен артық сандардың графигін береді.

Х = {3, 5, 7}, У = {4, 6} жиындарының элементтерінің арасындағы R – «артық» сәйкестігі берілсін. Сонда R = {5,4}, {7,4}, {7, 6} және оның графы 5 - сызбадағыдай болады.

Осы графтағы стрелкалардың бағытын кері өзгертейік. Сонда У және Х жиындарының элементтерінің арасындағы «кем» сәйкестігінің графигі алынады (6 - сызба).

---

Смотрите также файлы

• Язык танца Содержание.pptx

• Проверочный тест Августин и Фома Аквинский.docx

• Контрольная работа по дисциплине Библиотековедение Лапчук И. А., студентка 2ого курса, заочного отделения.docx

• Тестовое задание для 10 б класса Задание.docx

• Практическая работа Приемка товаров по количеству Цель приобрести навыки в документальном оформлении результатов приемки.docx