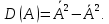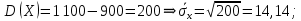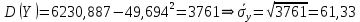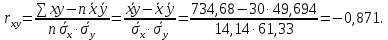Файл: ММ20Э191 Студент В. Ю. Ирбулдин москва 2022 Вопросы Укажите основные этапы эконометрического исследования.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 04.12.2023

Просмотров: 42

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Автономная некоммерческая организация высшего образования

«МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»

Кафедра экономики и управления
Форма обучения: заочная/очно-заочная
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙПО ДИСЦИПЛИНЕЭКОНОМЕТРИКАГруппа ММ20Э191СтудентВ.Ю. ИрбулдинМОСКВА 2022Вопросы:1. Укажите основные этапы эконометрического исследования. Ответ:a. Спецификация модели — выбор класса моделей, наиболее подходящих для изучения процессов и явлений. Спецификация, в свою очередь, делится на 2 подэтапа: отбор существенных факторов и выбор пита модели.b. Оценка параметров моделиc. Проверка качества построенной модели.2. Назовите виды аналитических зависимостей, наиболее часто используются при построении моделей.Ответ:Наиболее часто используются следующие виды аналитических зависимостей: линейная, степенная, полулогарифмическая, гиперболическая и экспоненциальная.a. линейная 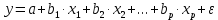,b. степенная 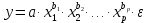,c. полулогарифмическая 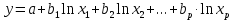,d. гиперболическая 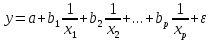,e. экспоненциальная 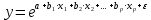,3. Охарактеризуйте функции, которые чаще всего используются для построения уравнения парной регрессии.
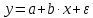
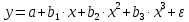
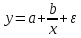
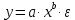
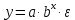
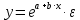
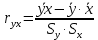
Ответ:Линейная регрессия: Регрессии, нелинейные по объясняющим переменным:полиномы разных степенейравносторонняя гипербола Регрессии, нелинейные по оцениваемым параметрам:степеннаяпоказательная экспоненциальная 4. Укажите, по какой формуле вычисляется выборочный коэффициент парной корреляции rxy.Ответ:Выборочный парный коэффициент корреляции rxyгде 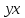- среднее арифметическое произведения факторной и результативной переменных: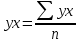 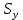– выборочное среднеквадратическое отклонение результативной переменной у, показывающее, на сколько единиц в среднем отклоняются значения результативной переменной 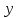от ее среднего значения 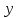–: – 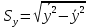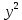среднее значение из квадратов значений результативной переменной 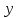: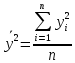5. Объясните сущность метода анализа динамического ряда.Ответ:Анализ динамических рядов проводится с целью выявление закономерности изменения изучаемого явления во времени, а также, для прогнозирования (экстраполирование) полученных данных на последующие годы.
Задачи:1. Рассчитать коэффициенты для различных видов зависимостей. Исходные данные в табл.3Таблица 3. Регрессионный анализ.

Значения вел X

№ варианта
10
20
30
40
50

1
7,38
18,15
44,64
109,79
270,06

2
30
50
70
90
110

3
23,94
58,95
99,87
145,16
194,01

4
126,19
54,92
33,77
23,91
18,29

5
166,44
55,41
18,44
6,14
2,04
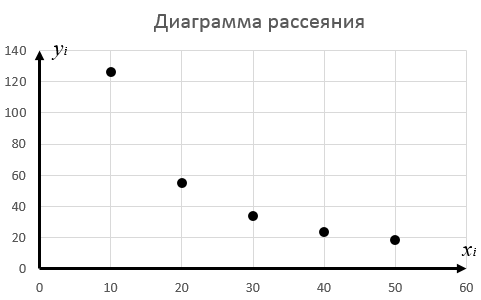
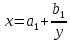
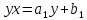
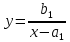
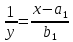
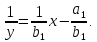
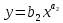
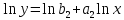
Строим диаграмму рассеянияВыделяем по виду диаграммы предполагаемые зависимости и линеаризуем их: 1. Сдвинутая обратно пропорциональная:2. Степенная:Рассчитываем коэффициенты методом МНК линейного уравнения регрессии 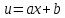, для чего строим вспомогательную таблицу, в последней строке приведено среднее значение столбца:

Значение вел X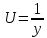


UX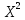


10
0,0079
0,0792
100

20
0,0182
0,3642
400

30
0,0296
0,8884
900

40
0,0418
1,6729
1600

50
0,0547
2,7337
2500

30
0,0304
1,1477
1100
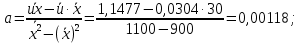
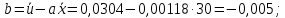
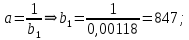
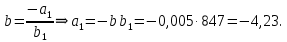
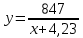
Получено уравнение регрессии:Рассчитываем коэффициенты методом МНК линейного уравнения регрессии 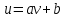, для чего строим вспомогательную таблицу, в последней строке приведено среднее значение столбца:


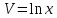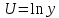UV


2,303
4,838
11,139
5,302

2,996
4,006
12,001
8,974

3,401
3,520
11,971
11,568

3,689
3,174
11,710
13,608

3,912
2,906
11,370
15,304

3,260
3,689
11,638
10,951
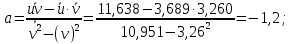
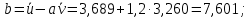
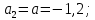
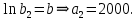
Получено уравнение регрессии:

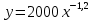
  1. Вычислить коэффициент корреляции для линейной зависимости. Исходные данные в таблице 4.
Таблица 4. Корреляционный анализ.

Значения вел X

№ варианта
10
20
30
40
50

1
7,38
18,15
44,64
109,79
270,06

2
30
50
70
90
110

3
23,94
58,95
99,87
145,16
194,01

4
126,19
54,92
33,77
23,91
18,29

5
166,44
55,41
18,44
6,14
2,04
Аналогично, строим таблицу:

Значение вел X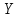


YX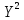




10
166,44
0,0792
100
27702,27

20
55,41
0,3642
400
3070,268

30
18,44
0,8884
900
340,034

40
6,14
1,6729
1600
37,7

50
2,04
2,7337
2500
4,162

30
49,694
734,68
1100
6230,887
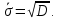
Находим средние квадратические отклонения как:Находим дисперсии:

Смотрите также файлы