ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 18
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Конспект урока геометрии
7 класс
Тема «Задачи на построение»
Кулакова Татьяна Михайловна,
учитель математики
ГБОУ ООШ № 15
г. Новокуйбышевска
Тема урока «Задачи на построение»
Тип урока - урок изучения нового материала, первичное закрепление новых знаний.
Цели урока: 1) дать представление о задачах на построение;
2) рассмотреть наиболее простые задачи на построение и научить
учащихся решать их.
Задачи урока:
-
Образовательные:-
познакомить учащихся с задачами на построение; -
сформировать умение решать простые задачи на построение; -
расширить знания об истории геометрии.
-
-
Воспитательные:-
воспитание ответственного отношения к учебному труду, воли и настойчивости для достижения конечных результатов при изучении темы; -
воспитание интереса к истории математики, как науки.
-
-
Развивающие:
-
развитие навыков самоконтроля; -
формирование алгоритмического мышления.
Оборудование к уроку:
-
Компьютер, с минимальными техническими требованиями: Windows 95/98/ME/NT/2000/XP, Internet Explorer 5.0, Pentium-150, 100 Мб свободного дискового пространства, 64 Мб оперативной памяти,
CD-ROM, SVGA 800
-
Видеопроектор, экран.
Домашнее задание: Геометрия ,7-9:Учеб. для общеобразоват. учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.-М., 2002. пп. 22-23, В. 17-21 стр.50,задача 5(стр. 48), задача 6 (№153).
План урока:
I.Организационный момент (приветствие, проверка готовности к уроку, постановка цели на урок,
инструктаж подготовки домашнего задания) – 1 мин.
II. Проверка теоретических знаний учащихся по теме « Окружность» - 5 мин.
III. Изучение нового материала
3.1. Актуализация опорных знаний – 5 мин.
3.2. Основные задачи на построение – 10 мин.
3.3. Отработка навыков решения задач на построение – 12 мин.
3.4. Три классические задачи древности – 3 мин.
IV. Оценка знаний учащихся, подведение итогов урока (рефлексия) – 4 мин.
Ход урока:
I. Организационный момент. Тема сегодняшнего урока - «Задачи на построение».
Цель урока – рассмотреть наиболее простые задачи на построение, которые решаются только с помощью циркуля и линейки без делений; научиться решать их.
Поэтому домашнее задание следующее:пп. 22-23, В. 17-21 стр.50,задача 5(стр. 48), задача 6 (№153).
II. Проверка теоретических знаний учащихся по теме окружность.
Мы с вами изучили тему « Окружность» и сегодня проверим с помощью теста ваши знания. Обратитесь к мониторам компьютера и ответьте на вопросы теста. Самостоятельно оцените свои знания, подсчитав количество верных ответов. Если верных ответов 5- оценка «5», если верных ответов 4 – оценка «4», если верных ответов 3 – оценка «3», если верных ответов 2 – оценка « 2».



III. Изучение нового материала.
3.1. Актуализация опорных знаний.
В домашней работе у вас была такая задача: Начертите треугольник АВС такой. что АВ = 3,6 см, АС = 2,7 см,
Итак, мы использовали линейку с миллиметровыми делениями и транспортир. Но есть такие задачи, в которых бывает оговорено, с помощью каких инструментов нужно построить предлагаемую геометрическую фигуру.
Задача 1. С помощью циркуля и линейки без делений на данном луче от его начала отложить отрезок, равный данному. Чертёж на экране.

Учащиеся предлагают варианты решений.
А теперь проверим ваше решение (см. слайд)

Вывод: Очень многие построения в геометрии могут быть выполнены с помощью циркуля и линейки без делений. Такие задачи мы будем называть задачами на построение.
3.2. Основные задачи на построение.
На экран проецируются слайды.



Мы уже решили задачу № 1.Теперь с помощью компьютера рассмотрим решение задачи № 2. Выполняйте соответствующие построения в тетради.



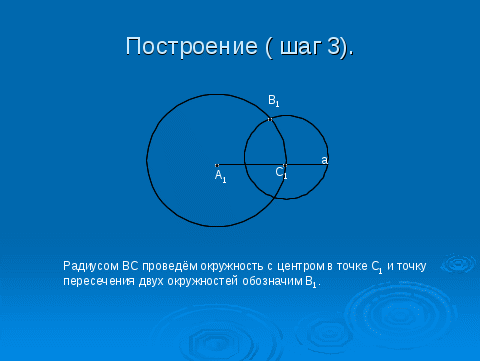

3.3. Отработка навыков решения задач на построение.
На экране монитора вы видите решение задачи № 3 «Построение биссектрисы данного угла».
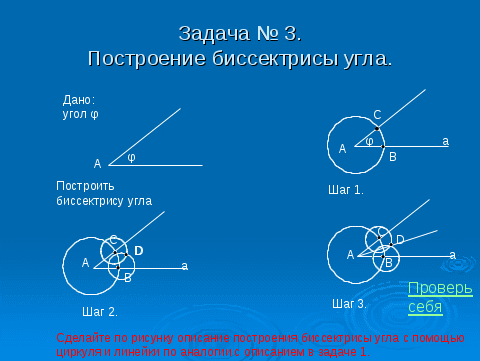
Сделайте по рисунку описание построения биссектрисы угла с помощью циркуля и линейки по аналогии с описанием, представленным при решении задачи № 2.
Проверьте себя.

Теперь рассмотрим решение задачи № 4, выполняя соответствующие построения в тетрадях.
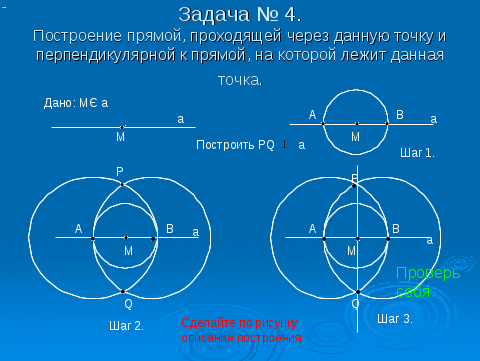
Сделайте по рисунку описание построения по аналогии с описанием построения угла, равного данному.
Проверьте себя.

Выводы: на сегодняшнем уроке мы познакомились с простейшими задачами на построение с помощью циркуля и линейки. Дома вам предстоит самостоятельно по учебнику разобрать решение двух задач 4 и 5.
3.4. Три классические задачи древности.
Обратимся к истории математики.

Древнегреческие математики достигли чрезвычайно большого искусства в геометрических построениях с помощью циркуля и линейки. Однако три задачи не поддавались их усилиям.
Есть задачи на построение, про которые известно, что они неразрешимы с помощью циркуля и линейки.

Вы можете перейти по желанию на следующие слайды, которые содержат информацию для ознакомления с данными задачами.



IV. Подведение итогов урока (рефлексия).
Мы изучили много нового, узнали какие задачи можно решить только с помощью циркуля и линейки. У вас у каждого лежит лист с вопросами. Оцените свою работу на сегодняшнем уроке, выбрав один из предложенных вариантов ответа.
-
Оцените степень сложности урока. Вам было на уроке:-
легко; -
обычно; -
трудно.
-
-
Оцените степень вашего усвоения материала:
-
усвоил полностью, могу применить; -
усвоил полностью, но затрудняюсь в применении; -
усвоил частично; -
не усвоил.
Собрать листочки для оценки степени усвоения материала сегодняшнего урока, чтобы на следующем уроке правильно организовать работу.
Сообщаются оценки за урок, включая оценки за тест по теме « Окружность».
Выводы и методические рекомендации по изучению данной темы.
В соответствии с первым вариантом тематического планирования учебного материала на изучении темы « Задачи на построение» отводится 2 часа. В зависимости от степени усвоения материала учащимися можно использовать урок из отведённых для решения задач по теме «Треугольники». Назначение параграфа
« Задачи на построение» состоит в том, чтобы дать представление о новом классе задач – построение геометрических фигур с помощью циркуля и линейки без масштабных делений – и рассмотреть основные ( простейшие ) задачи этого типа.
Неслучайно задачам на построение предшествует рассмотрение окружности и её элементов. Поэтому в начале своего урока я провожу тест по теме «Окружность», где проверяется, знают ли учащиеся элементы окружности и смогут ли использовать эти знания при решении задач на построение.
Задачи на построение с помощью циркуля и линейки являются традиционным материалом, изучаемым в курсе планиметрии. Обычно эти задачи решаются по схеме, приведённой в разработке урока. Сначала рисуют(чертят) искомую фигуру и устанавливают связи между данными задачи и искомыми элементами. Эта часть решения называется анализом. Она даёт возможность составить план решения задачи. Затем по намеченному плану
Затем по намеченному плану выполняется построение циркулем и линейкой, после этого нужно доказать, что построенная фигура удовлетворяет условиям задачи. И, наконец, необходимо исследовать, при любых ли данных эта задача имеет решение, и если имеет, то сколько решений.
В тех случаях, когда задача достаточно простая, отдельные части, например анализ или исследование, можно опустить. В 7 классе при решении задач на построение рекомендуется ограничиваться только выполнением построения.
В отдельных случаях можно провести устно анализ и доказательство, а элементы исследования должны присутствовать лишь тогда, когда это оговорено условием задачи. Учащимся, проявляющим повышенный интерес к математике, полезно решать задачи на построение по полной схеме.
На уроках по этой теме нужно прежде всего отработать навыки решения простейших задач на построение циркулем и линейкой, рассмотренных в учебнике
(они перечислены в разработке урока).
На первом уроке изучения этой темы мы рассмотрели 4 из 6 простейших задач, две оставшиеся задачи учащиеся должны разобрать по учебнику самостоятельно. В конце урока я прошу учащихся оценить степень усвоения материала, чтобы правильно построить следующий урок.
На следующем уроке следует закрепить навыки решения простейших задач на построение, научить решать задачи на построение.
В начале урока провести теоретический опрос по вопросам 18-21 и задачам 5, 6. Наиболее подготовленным учащимся можно дать решить задачи на построение № 2-6 (см. план предыдущего урока) с доказательством самостоятельно. Также провести фронтальную работу с менее подготовленными учащимися – повторить решение задач на построение № 1-6 (см. там же) у доски и в тетрадях учащихся без доказательства. Далее со всеми вместе решить задачу № 150, 151 и 155 из учебника.