Файл: Решение 1 Клин можно считать пленкой переменной толщины. Когерентные лучи 1 и 2 получаются в этом случае при отражении от нижней и верхней грани клина Рис отражение когерентных лучей от граней клина.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 26
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
№1
Вертикально-расположенная мыльная пленка образует клин, угол которого
составляет 25,2 секунды (25,2"). В отражённом свете наблюдаются полосы
равной толщины. Длина волны монохроматического света равна 650 нм, что
соответствует красному цвету. Показатель преломления пленки n = 1,33. Сколько красных полос наблюдается на участке длиной 1 см? Свет на поверхность клина падает нормально. Изобразите ход лучей в клине, рисунком поясните, какие лучи интерферируют в этом случае.
Дано:
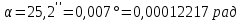
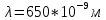n = 1.33l = 0.01 м
Найти:
N - ?
Решение
1)Клин можно считать пленкой переменной толщины. Когерентные лучи 1 и 2 получаются в этом случае при отражении от нижней и верхней грани клина
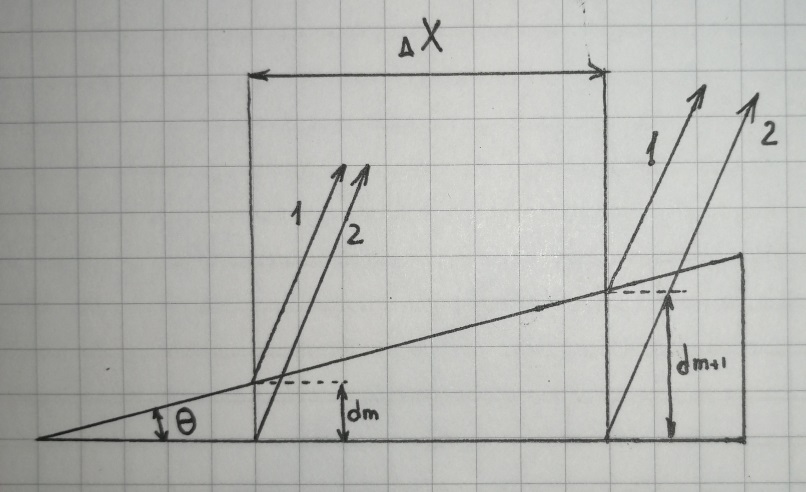
Рис.1. отражение когерентных лучей от граней клина
2)Так как интерференция на клине наблюдается при малых преломляющих углах клина, лучи, отраженные от верхней и нижней граней, можно считать параллельными.
3)Оптическая разность хода двух лучей складывается из разности оптических длин путей этих лучей
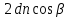и половины длины волны, представляющей собой добавочную разность хода, возникающую при отражении от оптически более плотной среды => условие интерференции для минимума излучения может быть записано в виде:
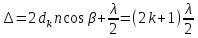(1)Где п – показатель преломления стекла,
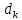- толщина клина в том месте, где наблюдается темная полоса, соответствующая порядку k, 
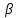- угол преломления, 
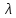- длина волны излучения.Учитывая, что угол падения равен
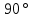, косинус этого угла составит тогда 1, то:
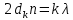Пусть темной полосе, порядок которой равен k + N соответствует толщина 
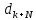, тогда учитывая малость преломляющего угла призмы можно записать: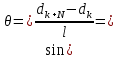
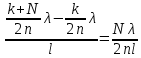(2)Тогда можно записать, что ширина интерференционной полосы составит:
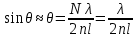При интерференции от клина мы можем записать формулу, которая описывает данный процесс:
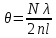Откуда получим, что число линий на 1 см длины составит:
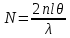Подставим числовые данные в полученную формулу:
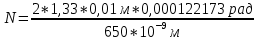N=5Ответ: число полос равно 5.
№2.
При освещении катода светом с длиной волны сначала
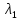= 440 нм, а затем 
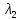= 680 нм обнаружили, что запирающий потенциал изменился в 3 раза. Определить работу выхода электрона 
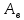= из катода. Сравните скорости электронов 
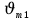и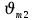 
, с которыми они вылетают из катода. Изобразите на рисунке вольтамперную характеристику фотоэффекта (ВАХ); покажите на ней ток насыщения 
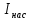и задерживающий потенциал 
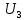.Дано:
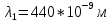
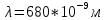
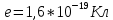
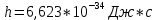
Найти:
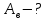
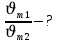
Решение
Для решения задания можно использовать формулу закона Эйнштейна для фотоэффекта.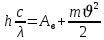
(1)Задерживающий потенциал, приложенный к фотоэлементу, будет тормозить поток фотоэлектронов и при некотором значении тормозящего напряжения приведет к тому, что все электроны будут тормозится и фототок исчезнет.
Тогда можно записать:
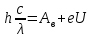
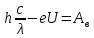
В таком случае для первого и второго облучения катода можно записать: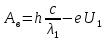
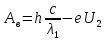Поскольку запирающий потенциал изменился в 3 раза, то приравняв формулы мы получим равенство: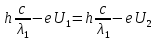
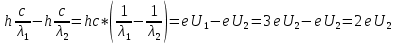
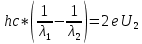
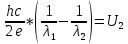
Вычислим величину задерживающего потенциала, подставив в полученную формулу данные в условии числовые значения: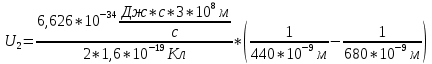
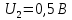
=>работа выхода электрона составит:
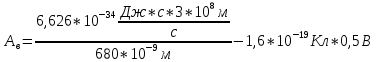
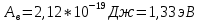
Отношение скоростей фотоэлектронов составит: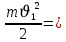
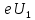
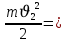
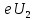
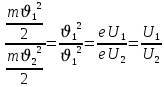
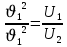
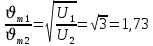
Допустим, что фотоэлемент включен в цепь. Передвигая движок потенциометра и снимая показания приборов, можно найти вольтамперную зависимость фотоэлемента. При 0 U через элемент проходит небольшой ток. Под действием света из анода вырываются электроны, и он заряжается положительно. Вырванные электроны вблизи 3 анода создают отрицательно заряженное облако, из которого большая часть электронов попадает обратно на анод (анод при 0 U притягивает электроны), а часть электронов из облака попадает на катод. Они и создают небольшой ток. Для прекращения фототока необходимо приложить обратное по знаку напряжение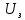 
, которое называют задерживающим напряжением. Если увеличивать напряжение, то по мере роста все большее число электронов за секунду попадает на катод. Облако из электронов вблизи анода редеет, а ток через фотоэлемент растет. При достаточно сильном поле облако из электронов вблизи анода полностью исчезнет. Все электроны, вымываемые из металла анода, будут попадать на катод - наступит насыщение: дальнейшее усиление поля в баллоне фотоэлемента не приведет к увеличению тока. Ток насыщения 
определяется тем количеством электронов, которые вырываются в секунду из металла.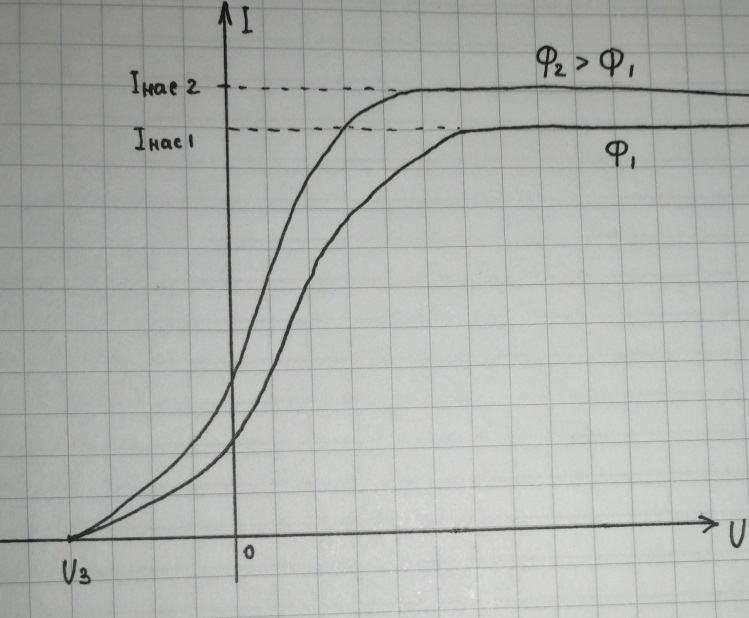
Рис.2. ВАХ фотоэффекта.
Ответ:
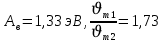
№3. Атомарный водород, находящийся в основном состоянии, облучается монохроматическим светом с энергией 15 эВ. Электроны, вылетающие из атомов в результате ионизации попадают в магнитное поле с индукцией 1 мТл перпендикулярно линиям индукции. Определить радиус окружности, по которой движутся электроны. Изобразите на рисунке энергетическую диаграмму атома водорода; на отдельном рисунке изобразите движение электронов в магнитном поле. Ответ
???? = 4 мм
Дано:
E=15 эВ
С=
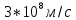
m=
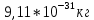
В=0,001 Тл
Найти:
R-?
Решение
Согласно условию задания поток фотонов ионизирует невозбужденный атомарный водород. В результате этого процесса мы получим ионы водорода.
Выбитые электроны имеют некоторую кинетическую энергию и скорость. Рассчитаем максимальную скорость электронов. Для этого вычислим значение энергии ионизации атома водорода, используя формулу:
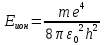(1)Подставив данные в условии числовые значения в формулу 1 получим
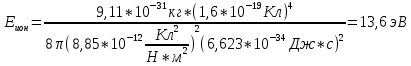Согласно закону сохранения энергии энергия фотона распределяется на ионизацию атома водорода и на кинетическую энергию электрона, тогда кинетическая энергия составит: 15 – 13,6 = 1,4 эВ.А скорость будет равна:
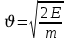(2)Подставим данные в условии числовые значения в формулу 2
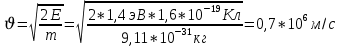Поскольку скорость электрона на два порядка меньше скорости света, то релятивистскими эффектами возрастания массы можно пренебречь.Для решения данной задачи нужно рассмотреть движение микрочастицы в магнитном поле и зависимости, которые описывают его движение в магнитном поле с индукцией В или напряженность поля Н.
Для этого выполним рисунок:
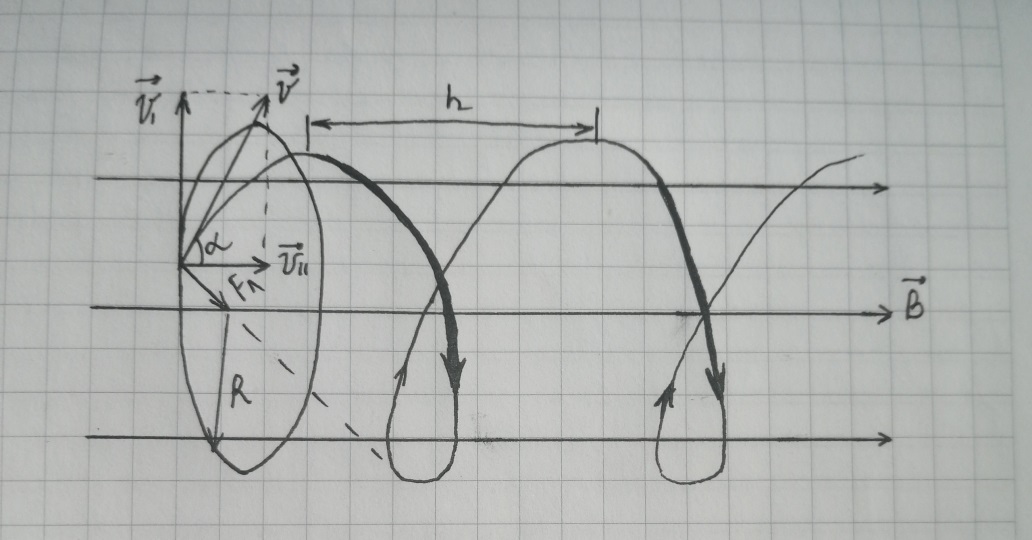
В магнитном поле микрочастица, как и любая заряженная частица, будет двигаться по винтовой линии. Сила Лоренца действует на нее в плоскости перпендикулярной вектору индукции магнитного поля и предоставляет ему центростремительное ускорение.
Тогда можно записать:
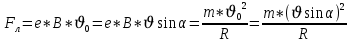(3)
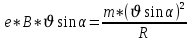Упростим формулу с учетом того, что 