Добавлен: 05.12.2023
Просмотров: 14
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Владимирский государственный университет
имени Александра Григорьевича и Николая Григорьевича Столетовых»
(ВлГУ)
Кафедра функционального анализа и его приложений
ПРАКТИЧЕСКАЯ РАБОТА №1
по дисциплине
«Разделы математики»
На тему:
«Элементы математического анализа.»
Отчет выполнила:
Ст. гр. Арх-222
Рыжкина А.Д.
Вариант 15
Отчет проверила:
доцент каф. ФАиП
Кондакова Е.Н.
г. Владимир
2023 г.
Цель работы.
Получение и систематизация знаний по теме «Элементы математического анализа», а также навыков решения типовых задач.
Теория по теме: «Элементы математического анализа.»
Математический анализ – раздел исследования функциональных зависимостей.
Функциональные зависимости – зависимость одной независимой переменной от другой зависимой переменной («х» от «у»).
Функцию можно задать аналитически, графически и таблично.
1.Табличный способ — указание значений функции от соответствующих значений аргумента. Этот способ применяется в тех случаях, когда область определения функции состоит из конечного числа значений.
2.Графический способ представления функциональных зависимостей также является одним из средств их фиксации при изучении реальных явлений. Это, например, позволяют делать различные «самопишущие» приборы: сейсмограф, электрокардиограф, осциллограф и т.п.
3.Аналитический (формульный) способ — задание функции некоторой формулой, показывающей способ вычисления значения функции по соответствующему значению аргумента. Если при этом ничего не говорится об области определения, то считается, что функция определена на множестве тех значений аргумента
, для каждого из которых аналитическое выражение, задающее функцию, имеет смысл.
Свойствами функции являются:
1.Область определения.
2.Область значений.
3.Четность и нечетность.
4.Монотонность.
5.Ограниченность.
6.Периодичность.
Основными элементарными функциями являются:
1.Степенные
2.Показательные
3.Логарифмические
4.Тригонометрические
5.Обратные тригонометрические
Производная функции — это понятие дифференциального исчисления, характеризующее скорость изменения функции в данной точке. Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).
С помощью таблицы «производные от простейших элементарных функций» можно без труда преобразовать любую функцию, разбив ее на составляющие.
Преобразование графика функций:
-
Преобразование симметрии относительно оси абсцисс.
Если у нас есть произвольный график
, то для построения графика 
необходимо график симметрично отразить относительно оси 
(см. Рис. 2). Такое преобразование называется преобразованием симметрии относительно оси 
.Преобразование симметрии – зеркальное отражение относительно прямой. График
получается из графика функции 
преобразованием симметрии относительно оси
.-
Параллельный перенос вдоль оси ординат.
График
получается из графика функции
параллельным переносом последнего вдоль оси ординат на 
единиц вверх, если 
, и на 
единиц вниз, если 
.-
Растяжение от оси абсцисс и сжатие к оси абсцисс.
Чтобы построить график функции
, где 
и 
, нужно ординаты точек заданного графика умножить на 
. Такое преобразование называется растяжением от оси 
с коэффициентом , если 
, и сжатием к оси , если 
.-
Параллельный перенос вдоль оси абсцисс.
График
получается из графика функции 
параллельным переносом последнего на 
единиц влево, если 
, и на 
единиц вправо, если 
.-
Растяжение от оси ординат и сжатие к оси ординат.
График функции
, где и 
, получается из графика функции сжатием с коэффициентом к оси 
(если 
указанное «сжатие» фактически является растяжением с коэффициентом 
).-
Преобразование симметрии относительно оси ординат.
В этом случае график симметрично отображается относительно оси ординат, так как значения функций будут одинаковы при противоположных значениях аргумента.
Касательная прямая к кривой в точке
.
Прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка. Говоря общими словами, касательная прямая - это такая прямая, которая в данной конкретной точке наилучшим образом представляет кривую и ее направление в ней. Касательную прямую также можно определить, как предельное положение секущей прямой в данной точке.
Уравнение касательной к графику функции в точке:
y = f ’ (x 0) · (x − x 0) + f (x 0).
Нормалью к графику функции в точке называется прямая, проходящая через данную точку перпендикулярно касательной к графику функции в этой точке (понятно, что касательная должна существовать). Если совсем коротко, нормаль – это перпендикулярная к касательной прямая, проходящая через точку касания.
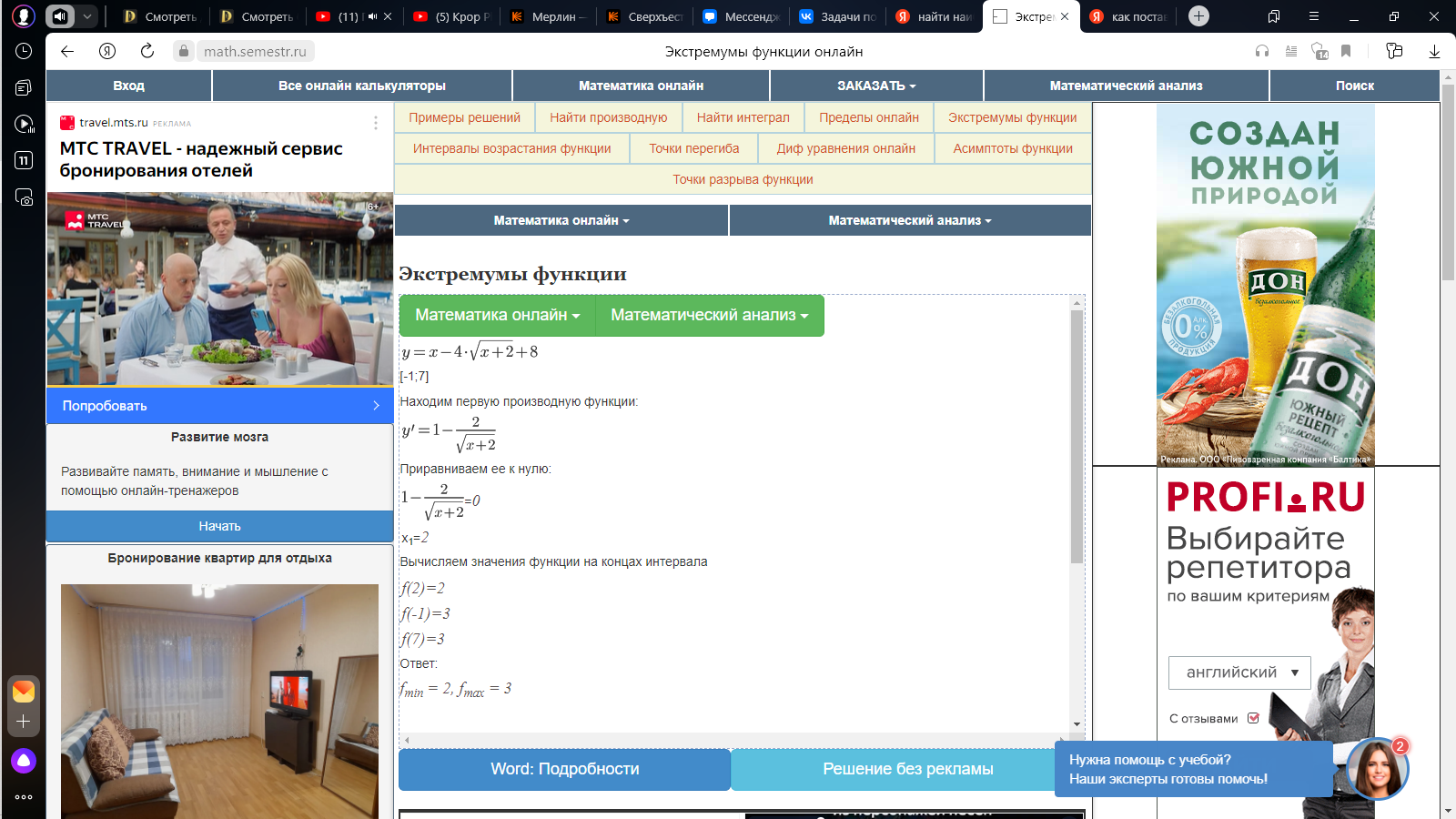
Уравнение нормали к графику функции в точке:
Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).
Онлайн проверка решений задач.
Задание 1.
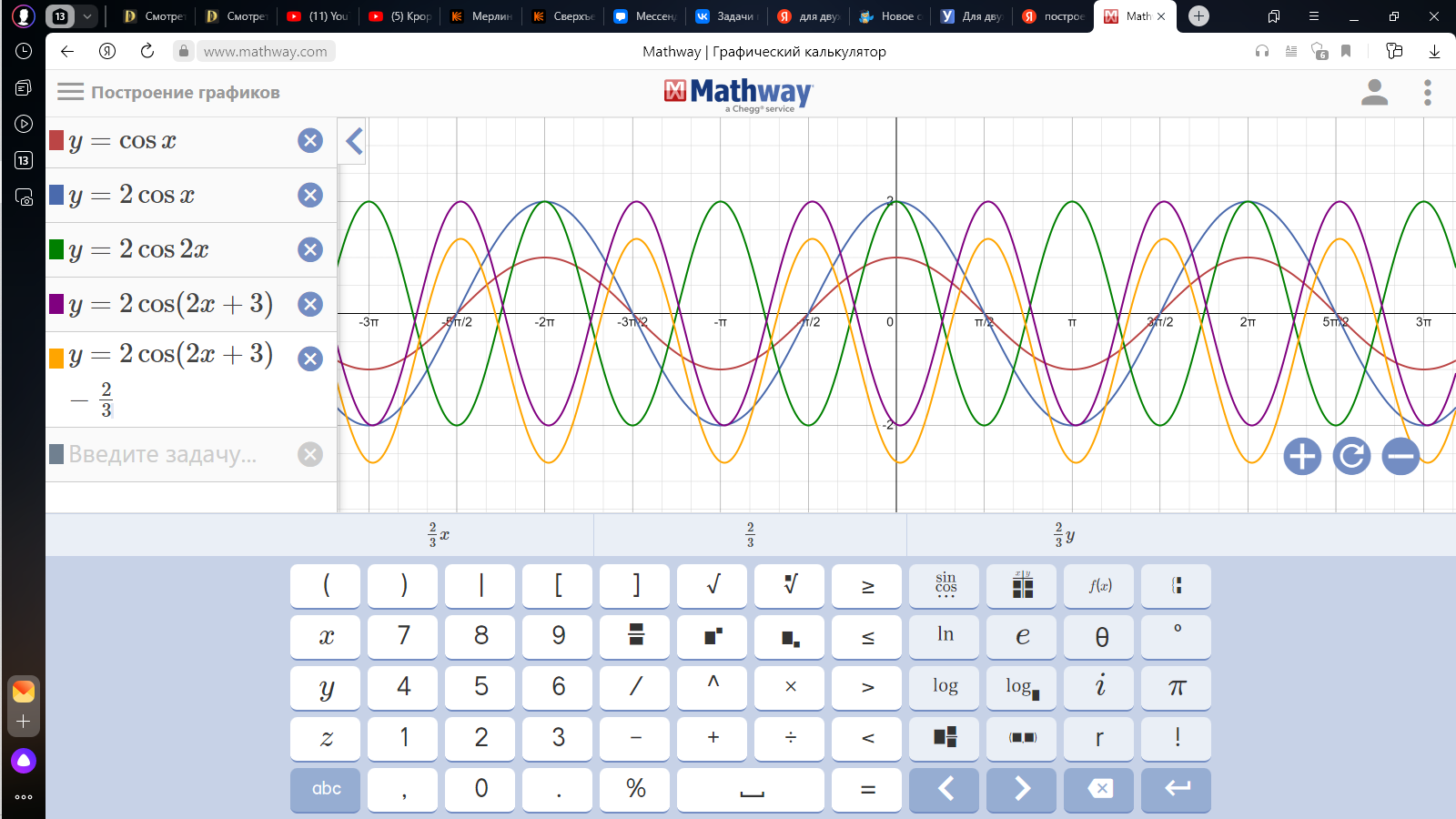
Задание 2.
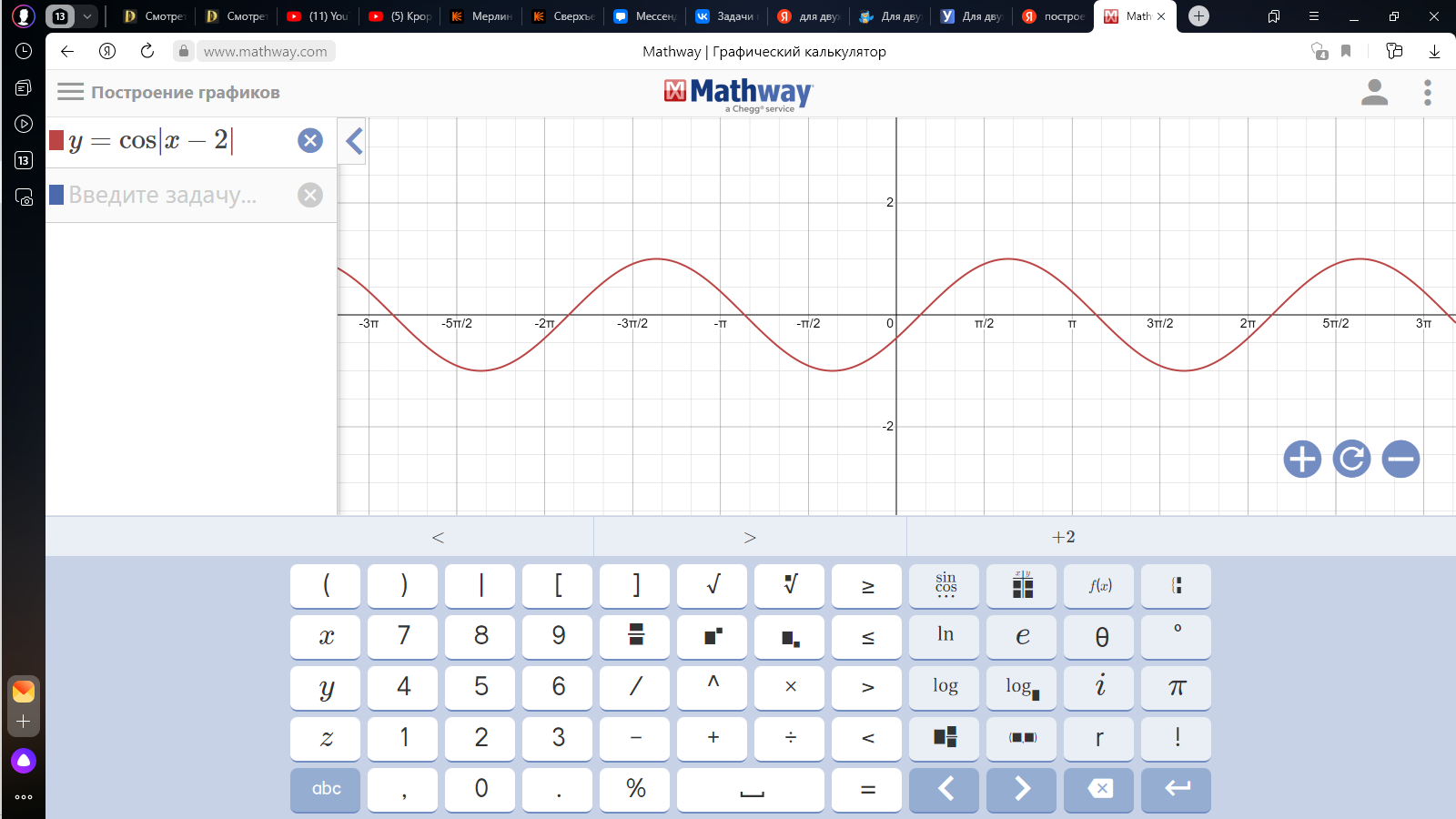
Задание 3.
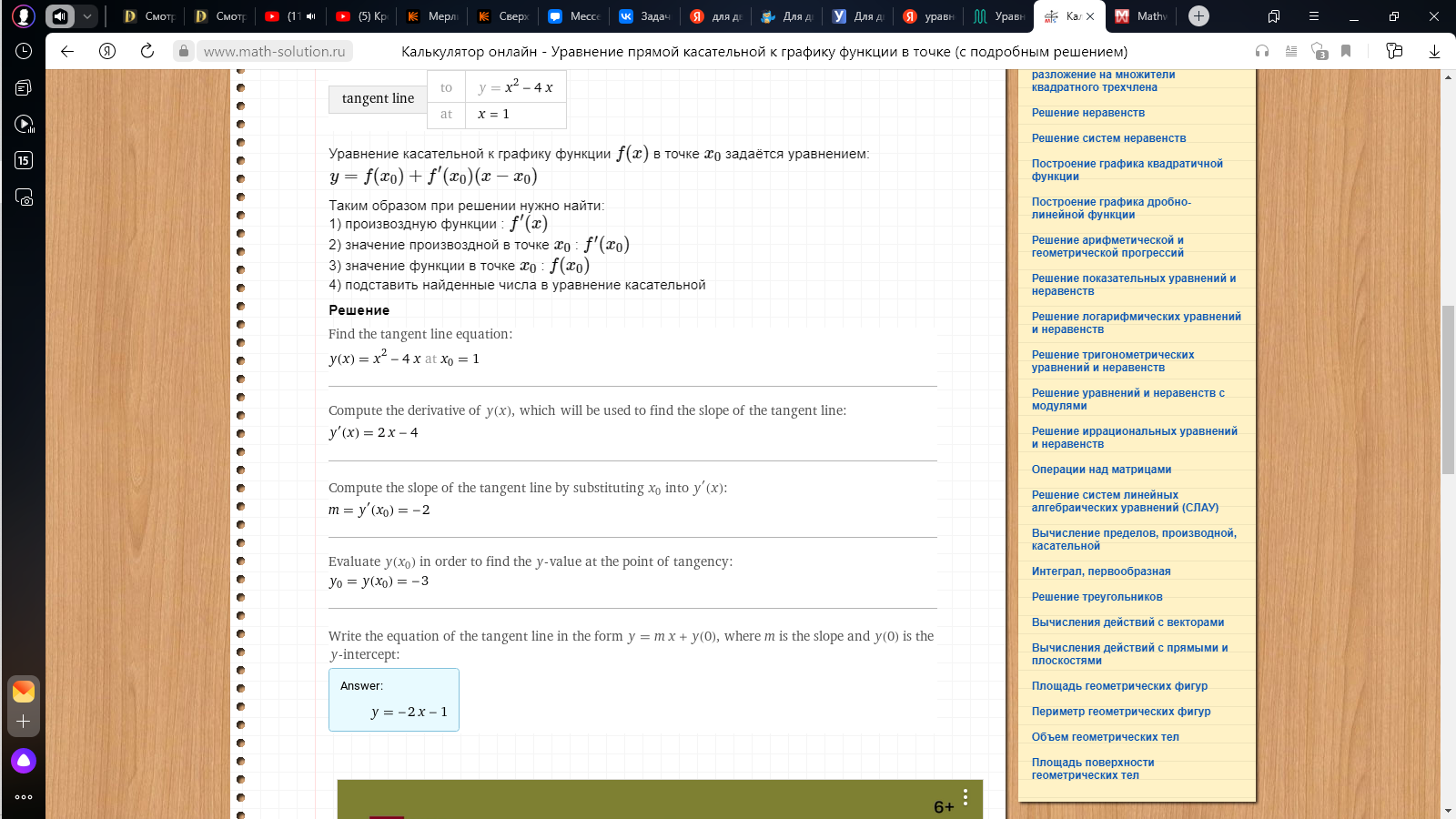
Задание 4.
