Федеральное государственное образовательное бюджетное учреждение высшего образования«Сибирский государственный университет телекоммуникаций и информатики»(ФГОБУ ВО «СибГУТИ»)Кафедра Безопасности жизнедеятельности и экологииКОНТРОЛЬНАЯ РАБОТА Теория вероятностейВыполнил: Чащина А.А.Группа: ТБТ-11Вариант: 4Проверила: Храмова Т.В.Новосибирск 2022Задание 1.В заданном слове буква «У» встречается 2 раза, буква «К» встречается 1 раз, буква «С» встречается 1 раз. Общее количество букв равно 4. 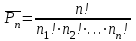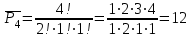По формуле перестановки с повторением: получим число перестановок (число различных 4-ти буквенных слов):Ответ. 12.Задание 2.A — произвольный автомобиль автопарка исправен; H₁ — автомобиль первой марки; H₂ — автомобиль второй марки; H₃ — автомобиль третьей марки; Вероятность события A вычисляем по формуле полной вероятности: P(A) = P(A|H₁)P(H₁) + P(A|H₂)P(H₂) + P(A|H₃)P(H₃) Вероятности: P(H₁) = 1/3 P(H₂) = 1/3 P(H₃) = 1/3 Условные вероятности заданы в условии задачи: P(A|H₁) = 0.8 P(A|H₂) = 0.7 P(A|H₃) = 0.85 P(A) = 0.8*1/3 + 0.7*1/3 + 0.85*1/3 = 0,7833.Ответ. 0,7833.Задание 3.

i	-4	1	2	3
pi	0.1	0.4	0.3	0.2

Математическое ожидание находим по формуле m = ∑x_ip_i.Математическое ожидание M[].M[] = (-4)*0.1 + 1*0.4 + 2*0.3 + 3*0.2 = 1.2Дисперсию находим по формуле d = ∑²_ip

---

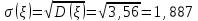
_i - M[]².Дисперсия D[].D[] = 4²*0.1 + 1²*0.4 + 2²*0.3 + 3²*0.2 - 1.2² = 3.56Среднее квадратическое отклонение σ().Задание 4.Вероятность попадания нормально распределенной случайной величины в заданный интервал вычисляется по формуле: 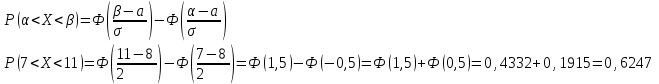Ответ. 0,6247.

---

Смотрите также файлы

• Курсовая работа внешняя политика петра первого выполнил(а) Студент(ка) группы ит11 ифф.doc

• Период командировки14 10 20 21 г. 24 11 2021 г. Основание командировки.doc

• Глебова Ирина Станиславовна Волкова Наталья Васильевна исследование социально экономических и политических процессов краткий конспект.pdf

• 2 Актуальность темы.pptx

• Медициналы генетика жне молекулалы биология кафедрасы.docx