ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 46
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
7. Организационная структура системы моделирования, во многом зависящая от сложности модели и уровня совершенства систем моделирования. Одним из последних достижений в области моделирования, возможно считать вариант применения имитационных моделей для проведения машинных экспериментов.
8. Пoведeнческaя страта, которая позволяет оценить верность достижения системой указанной цели. В зависимости от присутствия рандомных воздействий возможно разделять детерминированные и стохастические системы, по своему поведению — непрерывные и дискретные и т. д.. Явно, что поведение модели М не обязательно совпадает с поведением реального объекта, причем часто моделирование проводится на базе иного материального носителя.
9. Возможность развития модели, которая позволяет создавать более мощные системы моделирования S(M) исследования большинство сторон функционирования действительного объекта. Однако нельзя при конструировании системы моделирования ограничиваться только задачами нынешнего дня. Требуется предполагать возможность дальнейшего развития системы моделирования как в стороны расширения области изучаемых функций, так и расширения числа ее подсистем, т. е. полученная система моделирования должна давать возможность применять более новые современные методы и средства. Интеллектуальная система моделирования может функционировать лишь только совместно с группой людей, поэтому к ней предъявляют эргономические требования.
2.1. Цели моделирования систем управления.
Наиболее важным аспектом создания систем моделирования является проблема цели. Каждую модель строят в зависимости от цели, поставленную исследователем перед ней, отсюда одна из основных сложностей при моделировании — это проблема целевого объекта.
Для упрощения модели М цели подразделяют на подцели и создают эффективнейшие образцы моделей в зависимости от полученных подцелей моделирования. Возможно предоставить целый ряд примеров целей моделирования в области сложных систем. Например, для предприятий очень важно исследование процессов (быстрого) оперативного руководства производством, оперативно-календарного планирования, перспективного планирования и здесь также могут быть успешно применены методы моделирования.
Если цель моделирования усвоена, тогда возникает другая проблема, такая проблема как, проблема построения модели М. Построение модели оказывается возможным, если есть информация или выдвинуты предположения относительно структуры, алгоритмов, а так же параметров исследуемого объекта. На базе их изучения осуществляется определение объекта. Сейчас широко применяют различные способы оценки параметров: по методу наименьших квадратов, по методу максимального правдоподобия и другие.
Если модель М создана, тогда следующей проблемой можно считать сложность работы с ней, т. е. реализацию модели, основные задачи которой — минимизация времени получения итоговых peзультатов и обеспечение их правдивости.
Для верно созданной модели М характерным является то, что она выявляет лишь те закономерности, которые требуются исследователю, и не рассматривает свойства системы S, не важные для данного исследования. Необходимо отметить, что оригинал и модель должны быть одновременно похожи по одним признакам и различаться по другим, что позволяет извлечь важнейшие изучаемые свойства. В такой момент модель выступает как некий “заменитель” оригинала, обеспечивающий сохранение и изучение лишь определенных свойств реального объекта.
Если в момент моделирования значительное место занимает реальный физический эксперимент, то здесь очень важна и надежность используемых инструментальных средств, так как сбои и отказы программно-технических средств могут приводят к искажению значений выходных данных, отображающих ход процесса. Так же при проведении физических экспериментов необходимы специальная аппаратура, специально разработанное математическое и информационное обеспечение, позволяющие произвести диагностику средств моделирования, чтобы исключить такие ошибки в выходной информации, которые появились из за неисправности функционирующей аппаратуры. В процессе машинного эксперимента бывают и ошибочные действия человека-оператора. В таких условиях важные задачи стоят в области эргономического обеспечения процесса моделирования.
3. КЛАССИФИКАЦИЯ ВИДОВ МОДЕЛИРОВАНИЯ СИСТЕМ.
Основой моделирования является теория подобия, которая утверждает, что абсолютное подобие может присутствовать лишь при подмене одного объекта другим точно таким же. При моделировании точное подобие не имеет места и стремятся к тому, чтобы модель достаточно хорошо показывала изучаемую сторону функционирования объекта.
Классификационные признаки. Одним из первых признаков классификации видов моделирования стоит степень полноты модели и разделить модели в соответствии с этим признаком на полные, неполные и приближенные. В основе полного моделирования стоит полная идентичность, которая проявляется как во времени, так и в пространстве. При неполном моделировании характерно неполное подобие модели объекту. В основе приближенного
моделирования стоит приближенное подобие, при котором определенные стороны функционирования реального объекта не моделируются совсем.
Исходя из характера изучаемых процессов в системе S все виды моделирования могут разделяться на детерминированные и стохастические, статические и динамические, дискретные, непрерывные и дискретно-непрерывные. Детерминированное моделирование показывает детерминированные процессы, т. е. процессы, в которых отсутствует всякие случайные воздействия; стохастическое моделирование отражает вероятностные процессы и события. В данном случае проводится анализ ряда реализаций случайного процесса и оцениваются средние характеристики, т. е. набор однородных реализаций. Статическое моделирование необходимо для описания поведения объекта в определенный момент времени, а динамическое моделирование показывает действие объекта во времени. Дискретное моделирование требуется для описания процессов, которые подразумеваются дискретными, соответственно постоянное непрерывное моделирование позволяет показать непрерывные процессы в системах, а дискретно-непрерывное моделировании применяется для случаев, когда хотят выделить наличие как дискретных, так и непрерывных процессов.
В зависимости от формы отображения объекта (системы J можно выделить мысленное и реальное моделирование.
Мысленное моделирование обычно является единственным методом моделирования объектов, которые либо практически невыполнимы в заданном периоде времени, либо существуют вне условий, возможных для их физического создания. Например, на этапе мысленного моделирования может быть проанализировано множество ситуации микромира, которые не получается подвергнуть физическому эксперименту. Мысленное моделирование может быть проведено в вид наглядного, символического и математического.
Аналоговое моделирование базируется на применении аналогий различных уровней. Самым высшим уровнем является полная аналогия, имеющая место только для простых объектов. С увеличением сложности объекта используют схожести последующих уровней, когда аналоговая модель отражает несколько либо только одну сторону функционирования объекта.
Не последнее место при мысленном наглядном моделировании занимает макетирование. Мысленный макет может использоваться в случаях, когда происходящие в реальном объекте процессы не получается смоделировать физически, либо может предшествовать проведению других видов моделирования. Во главе построения мысленных макетов стоят аналогии, однако обычно базирующиеся на причинно-следственных связях между явлениями и процессами в объекте. Если добавить некое условное обозначение отдельных понятий, т. е. знаки, а также определенные операции между этими знаками, то возможно реализовать знаковое моделирование и с помощью знаков отражать набор понятий — составлять цепочки из слов и предложений. Применяя операции объединения, пересечения и дополнения теории множеств, возможно в отдельных символах выдать описание какого-то действительного объекта.
Тезаурус стоит основе языкового моделирования. Он образуется из набора понятий, причем этот набор должен быть закрепленным. Необходимо понимать, что между тезаурусом и обычным словарем имеются принципиальные различия. Тезаурус — словарь, который очищен от двоякости и неоднозначности, в нем каждому слову соответствует лишь единственное понятие, хотя в обычном словаре одному слову соответствуют несколько понятий.
Символическое моделирование выглядит как искусственный процесс создания логического объекта, который заменяет настоящий и выражает основные свойства его отношений с помощью некой системы знаков или символов.
Математическое моделирование. Для рассмотрения характеристик процесса функционирования любой системы S математическими методами, включая и машинные, необходимо провести формализацию этого процесса, т. е. построить математическую модель.
Под математическим моделированием нужно понимать процесс установления соответствия данному настоящему объекту некого математического объекта, именуемого математической моделью, и исследование этой модели, позволяющее получать параметры изучаемого реального объекта. Вид математической модели зависит не только от природы реального объекта, но и задач исследования объекта и необходимой правдивости (достоверности) и точности решения данной задачи. Любая математическая модель, как и всякая другая,
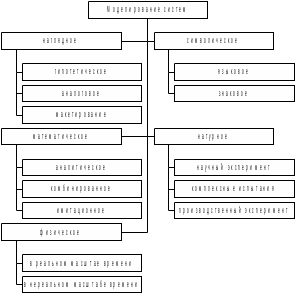
Рис 1. Классификация видов моделирования систем.
отображает реальный объект не полностью, а лишь с некоторой степенью приближения к действительности. Математическое моделирование для исследования характеристик процесса функционирования систем делится на аналитическое, имитационное и комбинированное.
В аналитическом моделировании процессы функционирования элементов системы записываются в виде функциональных соотношений (алгебраических, интегродиф-ференциальных, конечно-разностных и т. п.) или логических условий. Аналитическая модель исследуется следующими методами: а) аналитическим, когда пытаются получить в общем виде зависимости для искомых характеристик; б) численным, стремятся получить числовые результаты при конкретных начальных данных; в) качественным, когда, не имея решения в явном виде, находятся некоторые свойства решения (например, оценить устойчивость решения).
В определенных случаях исследования системы могут устроить и те выводы, которые можно сделать при использовании качественного метода анализа математической модели. Эти качественные методы достаточно широко применяются, например, в теории автоматического управления для оценки эффективности различных вариантов систем управления.
Заключение
В заключении работы попытаюсь сделать несколько выводов из материала написанном о моделировании в исследовании систем управления. Итак, определяем гносеологическую природу моделирования.
Определяя гносеологическую роль теории моделирования, т.е. ее значение в процессе понимания, требуется, отвлечься от имеющегося в науке и технике многообразия моделей и выделить то общее, что свойственно моделям различных по своей природе объектов реального мира. Это общее заключается в наличии некой структуры (статической или динамической, материальной или мысленной), которая идентична структуре данного объекта. В процессе исследования модель стоит в роли относительного самостоятельного квазиобъекта, позволяющего получить при исследовании некоторые знания о самом объекте.
В настоящее время в России управление и ее исследование идет по пути усложнения. Используя методы моделирования такие, как аналогия, возможно добиться неплохих результатов в хозяйственной деятельности предприятия. Аналогией называют высказывание о какой-либо идентичности двух объектов, при этом данное сходство может быть существенным и несущественным. Нужно отметить, что понятия существенности и несущественности сходства или различия объектов условны и относительны. Существенность сходства (различия) зависит от уровня абстрагирования и в общем случае определяется итоговой целью проводимого эксперимента. Современная научная теория создается, как правило, по аналогии с проверенными на практике научными положениями.
В заключении вышеизложенному, возможно подвести итог, что моделирование это главный путь в системе исследования систем управления и имеет наивысшую важность для менеджера любого уровня.
Список литературы.
-
Игнатьева А. В., Максимцов М. М. ИССЛЕДОВАНИЕ СИСТЕМ УПРАВЛЕНИЯ, Москва, 2000 -
Патерсон Дж. Теория сетей Петри и моделирование систем. — М.: Мир, 1984. -
Приикер А. Введение в имитационное моделирование и язык СЛАМП. — М.: Мир, 1987.
4.Советов Б. Я.. Яковлев С. А. Моделирование систем. — М.: Высшая школа, 1985.