Файл: Учебное пособие для вузов Дружининская И. М. Хованская И. А. Матвеев В. Ф. Мышкис П. А.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 258
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Почему, собственно, в этом случае нельзя пользоваться классическим определением вероятности
Если бы эта формула здесь работала, то ответ на поставленный вопрос был бы «ДА».
В чём же ошибка?
Исходы этого эксперимента никак нельзя назвать равновозможными.
Рассмотрим задачу, где легко совершить подобную ошибку.
Пример: Найти вероятность того, что в семье, имеющей четырёх детей, будет ровно три мальчика.
Неверноерешение:
В этой ситуации возможны 5 различных исходов (по возможному количеству мальчиков в семье, имеющей четырёх детей).
Благоприятен интересующему нас событию один исход (ровно три мальчика).
Значит, в соответствии с классическим определением вероятностей:
искомая вероятность р=1/5=0.2.
Здесь допущена ошибка: исходы в данном случае не будут равновозможными.
Верное решение задачи:
Подходящей Моделью случайного эксперимента для нашего примера "семьи, имеющей четырёх детей" могла бы быть "Модель четырех последовательных независимых испытаний Бернулли".
Отдельное испытание Бернулли с двумя исходами "успех" и "неудача" соответствует рождению каждого ребенка: "мальчик" или "девочка".
Каждый из этих исходов с высокой для нашей задачи точностью можно считать равновероятным.
Тогда, интересующее нас событие "в семье ровно три мальчика" в рамках нашей Модели будет представлено как событие: {X = 3},
"случайная величина X : "количество мальчиков в нашей семье"
(биномиальная случайная величина в схеме Бернулли с параметрами (4; 0.5), где количество испытаний 4, вероятность успеха 0.5 )
принимает значение 3".
Вероятность этого события С43(0.5)4 =4(0.5)4 , что не равна0.2.
Тестовые вопросы
-
Вероятность события, которое не может произойти, меньше 0. -
Вероятность события, которое не может произойти, не существует. -
Вероятность события, которое не может произойти, равна 0. -
Вероятность встретить на улице динозавра равна 0,5 – или встречу, или не встречу. -
Вероятность события, которое наверняка произойдёт, равна 1. -
Функция распределения положительной случайной величины определена при х>0. -
Интеграл интегральной функции распределения по всей прямой равен 1. -
Интегральная функция распределения определена для любой случайной величины. -
Интегральная функция распределения не определена для дискретной случайной величины. -
Интегральная функция распределения не определена для непрерывной случайной величины. -
Интегральная функция любой случайной величины не убывает. -
Интегральная функция любой случайной величины не возрастает. -
Интегральная функция любой случайной величины возрастает. -
Интеграл от плотности по всей прямой равен 1 -
Если р(х) – плотность распределения случайной величины Х, то р(х)<1 для всех х. -
Если р(х) – плотность распределения случайной величины Х, то р(х)>0 для всех х. -
Математическое ожидание любой случайной величины больше 0. -
Математическое ожидание любой случайной величины меньше 1. -
Дисперсия любой случайной величины меньше 1. -
Математическое ожидание неотрицательной случайной величины
больше 0. -
Математическое ожидание случайной величины меньше её дисперсии. -
Дисперсия отрицательной случайной величины не больше 0. -
Если Х и Y любые случайные величины, то Е(Х +Y)=Е(Х)+Е(Y). -
Если Х и Y любые случайные величины, то Е(ХY)=Е(Х)Е(Y). -
Если Х и Y любые случайные величины, то D(Х +Y)=D(Х)+D(Y). -
Если Х и Y любые случайные величины, то D(Х -Y)=D(Х)-D(Y). -
Если Х и Y любые независимые случайные величины, то
D(Х +Y)=D(Х)+D(Y). -
Если Х и Y любые независимые случайные величины, то
D(Х -Y)=D(Х)-D(Y). -
Если Х и Y любые независимые случайные величины, a и b любые числа,
то D(aХ +bY)=aD(Х)+bD(Y). -
Если Х и Y любые независимые случайные величины, a и b любые числа,
то D(aХ +bY)=a2 D(Х)+b2D(Y). -
Медиана любой случайной величины совпадает с её матожиданием. -
Мода любой случайной величины больше её матожидания. -
Матожидание любой случайной величины меньше её медианы. -
Если Х непрерывная случайная величина, то P(X>Med X)=0.5. -
Если Х непрерывная случайная величина, то P(X -
Если Х непрерывная случайная величина, то P(X=Med X)=0.5. -
Если Х непрерывная случайная величина, то P(X>Med X)=0 . -
Если Х непрерывная случайная величина, то P(X>Med X)=1 -
Среднеквадратичное отклонение всегда меньше дисперсии. -
Распределение Пуассона непрерывно. -
Случайная величина, распределённая по закону Пуассона, может принимать значение 3,7. -
Случайная величина, распределённая по экспоненциальному закону, не может принимать значение p -
Случайная величина, распределённая по экспоненциальному закону, может быть равна p. -
Для любых двух событий А и В Р(АВ)=Р(А)Р(В). -
Для любых двух событий А и В Р(А+В)=Р(А)+Р(В). -
Для любых двух событий А и В Р(А+В)=Р(А)+Р(В) – Р(А)(В). -
Для любых двух независимых событий А и В Р(АВ)=Р(А)Р(В). -
Для любых двух несовместных событий А и В Р(АВ)=Р(А)Р(В). -
Для любых двух независимых событий А и В Р(А+В)=Р(А)+Р(В). -
Для любых двух несовместных событий А и В Р(А+В)=Р(А)+Р(В). -
Для любых двух событий А и В Р(АВ)=Р(А)Р(В|А). -
Для любых двух событий А и В Р(АВ)=Р(А)Р(А|В). -
Р(А|А)=1. -
Р(В|В)=0. -
Выбирая случайным образом ответы (из двух альтернативных вариантов, содержащих правильный ответ) на 10 разных вопросов, вероятность ответить правильно на все вопросы равна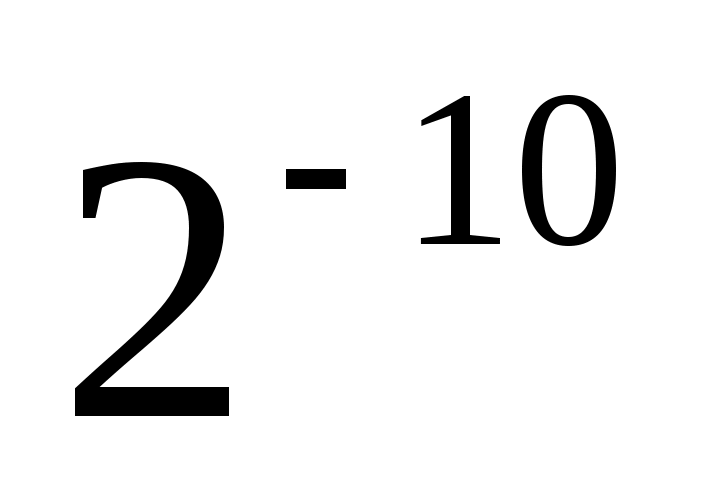 .
. -
Выбирая случайным образом ответы (из двух альтернативных вариантов, содержащих правильный ответ) на 10 разных вопросов, вероятность ответить правильно на 8 из них равна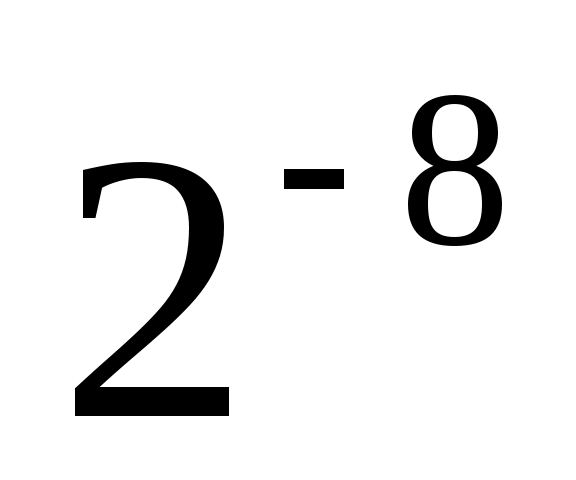 .
. -
Отвечая случайным образом на 10 вопросов, с двумя альтернативными вариантами ответов, вероятность правильно ответить на 8 из них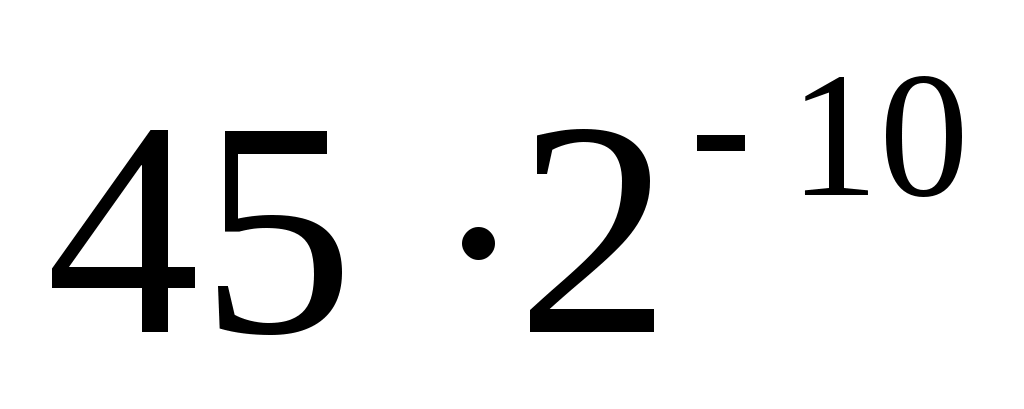 .
. -
Выбирая случайным образом ответы (из двух альтернативных вариантов, содержащих правильный ответ) на 10 разных вопросов, ответишь правильно на 8 из них с вероятностью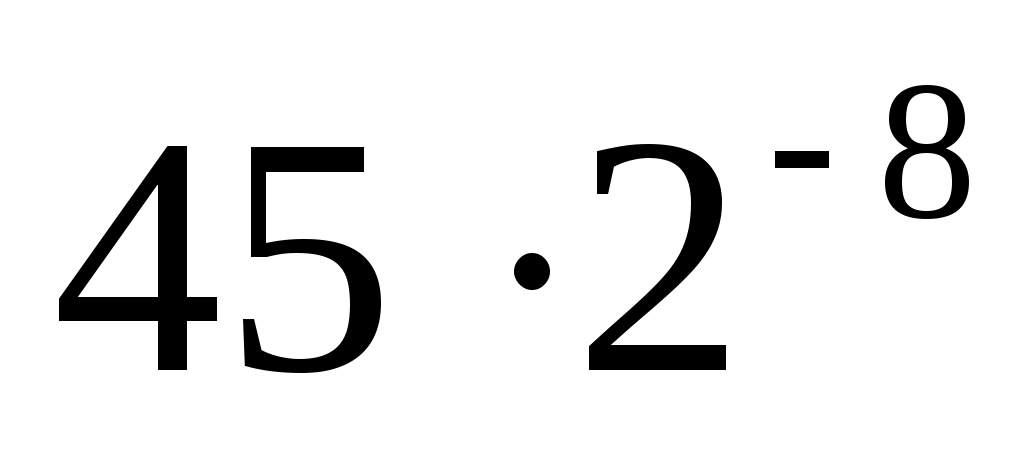 .
. -
Если МХ=5, DХ=16, то Х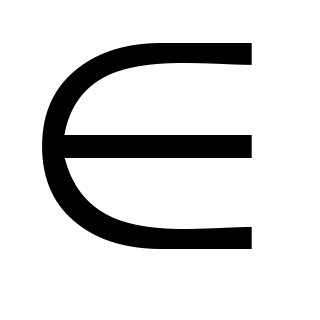 N(5;16) .
N(5;16) . -
Если вероятность выпадения 6 на игральной кости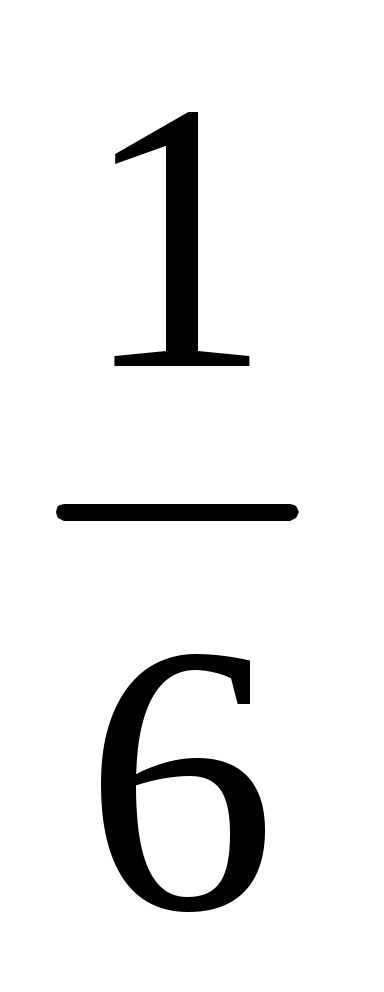 , то вероятность выпадение двух 6 подряд будет равна
, то вероятность выпадение двух 6 подряд будет равна 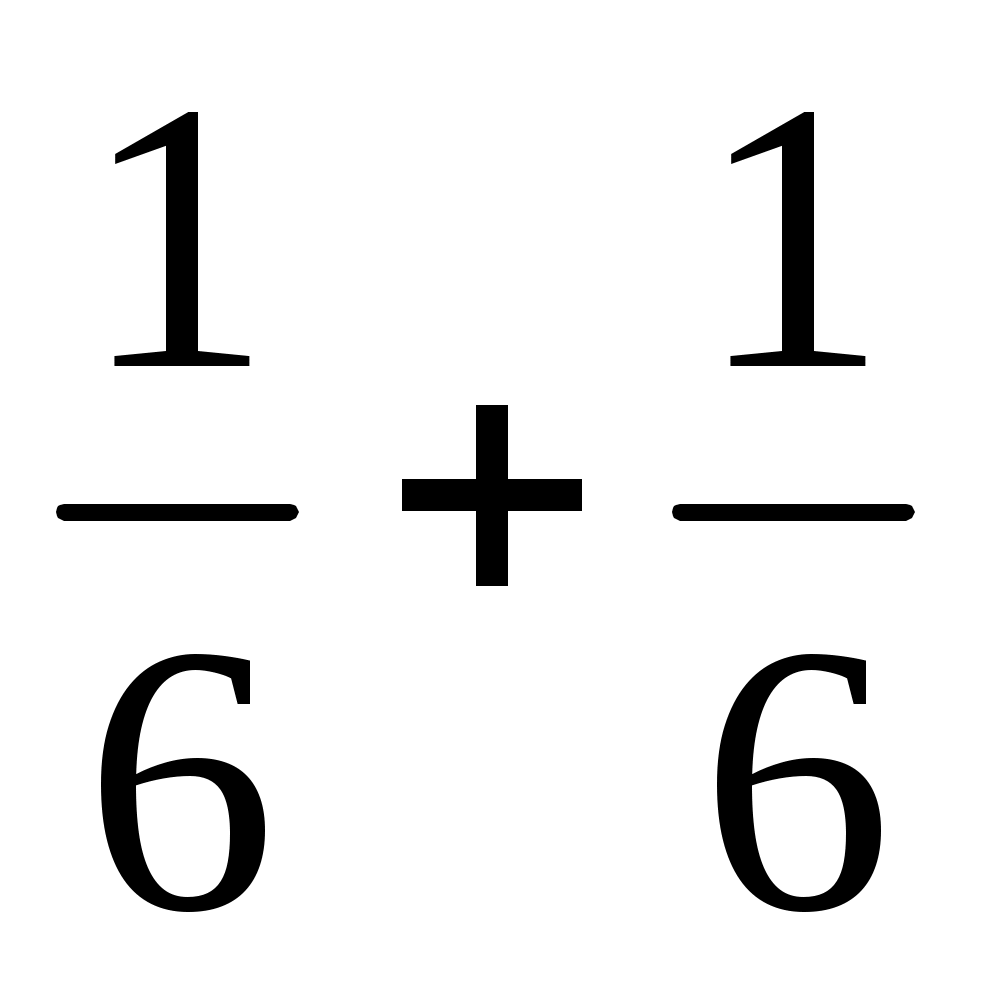 .
. -
Если вероятность выпадения 6 на игральной кости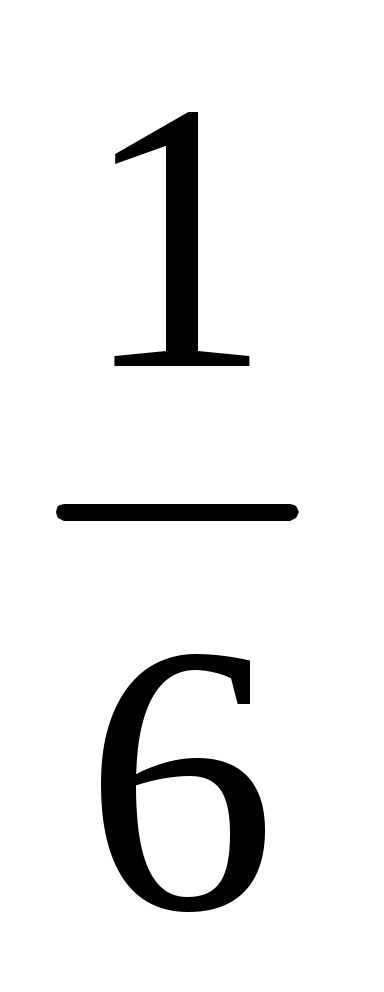 , то вероятность выпадения двух 6 при 3 бросаниях будет равна
, то вероятность выпадения двух 6 при 3 бросаниях будет равна 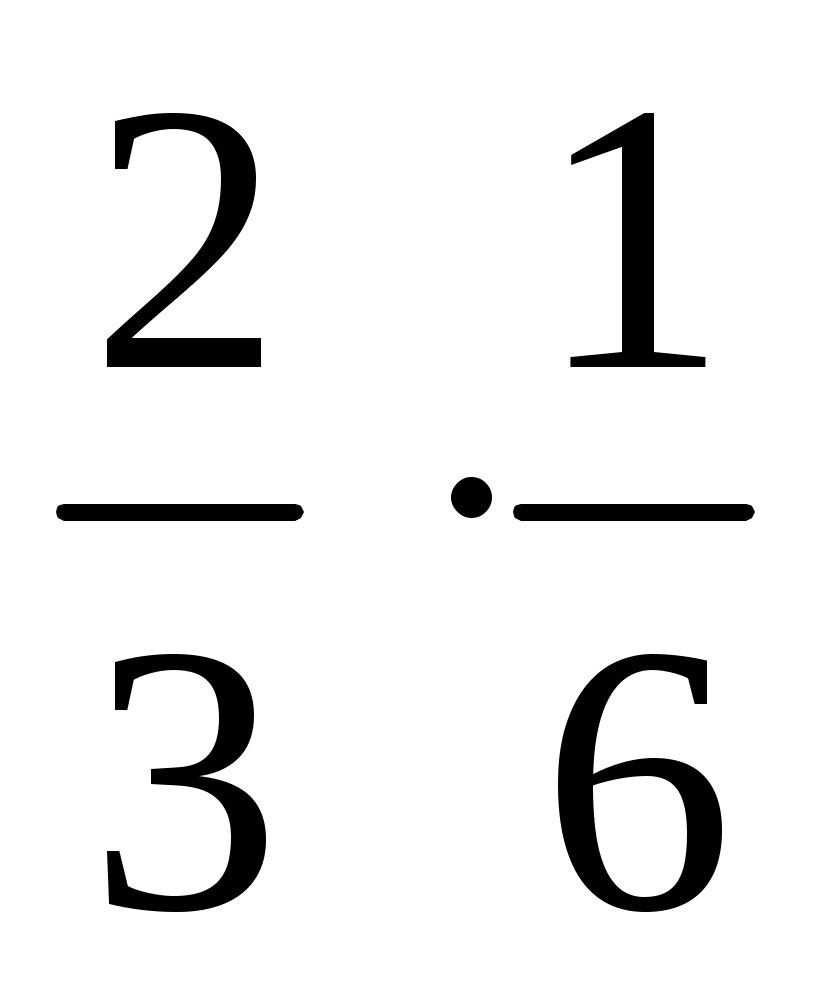 .
. -
Если вероятность выпадения 6 на игральной кости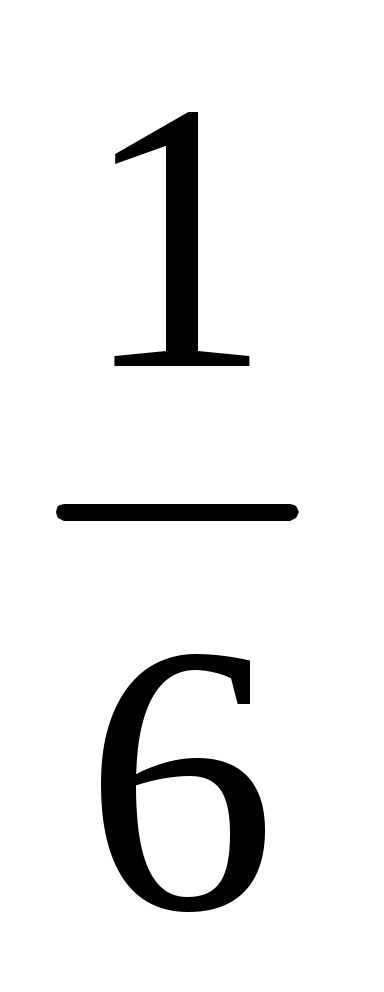 , то вероятность выпадения двух 6 при 3 бросаниях будет равна
, то вероятность выпадения двух 6 при 3 бросаниях будет равна 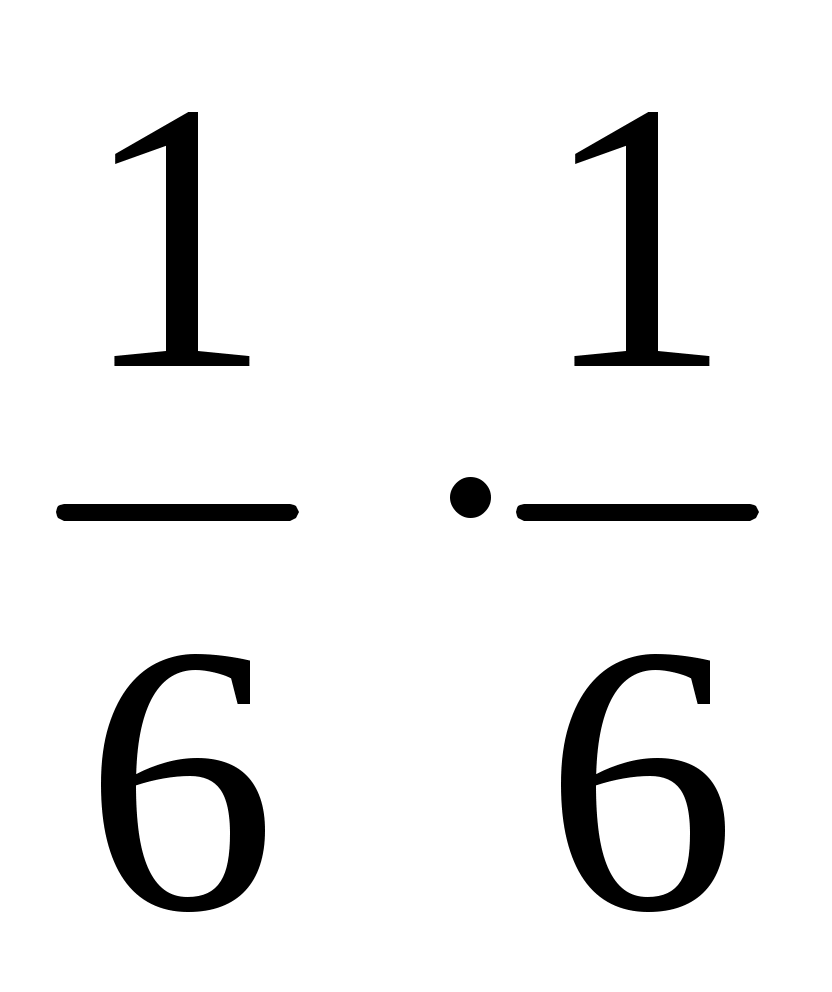 .
. -
Если вероятность выпадения 6 на игральной кости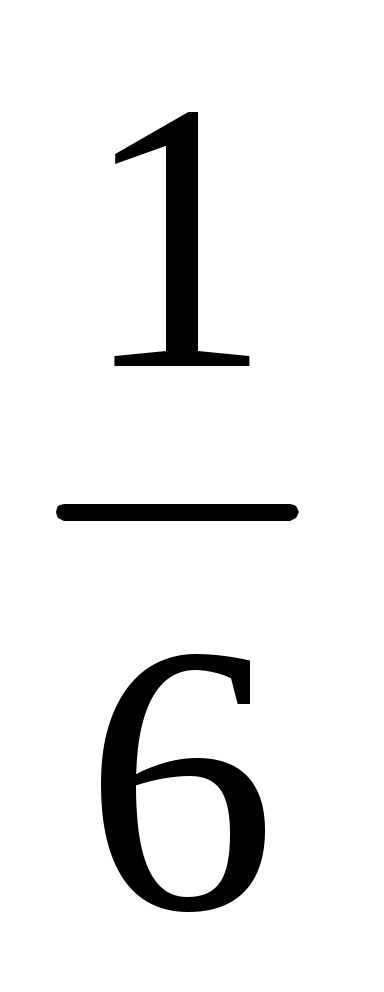 , то вероятность выпадения двух 6 при 3 бросаниях будет равна
, то вероятность выпадения двух 6 при 3 бросаниях будет равна 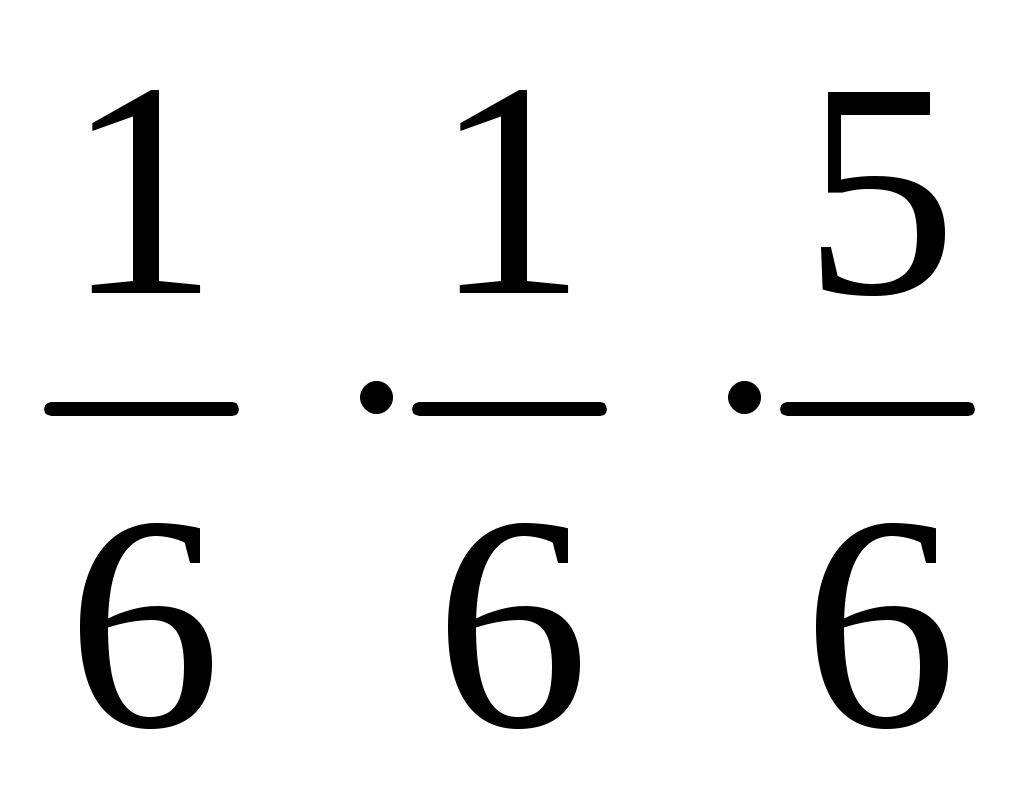 .
. -
Если вероятность выпадения 6 на игральной кости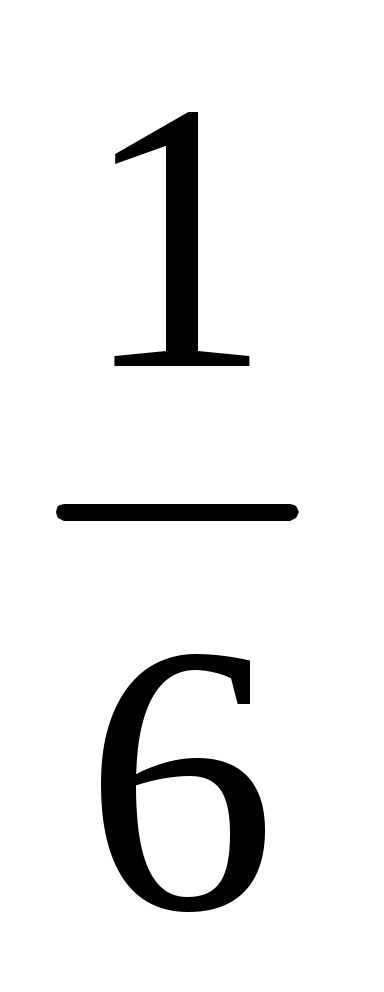 , то вероятность выпадения двух 6 при 3 бросаниях будет равна
, то вероятность выпадения двух 6 при 3 бросаниях будет равна 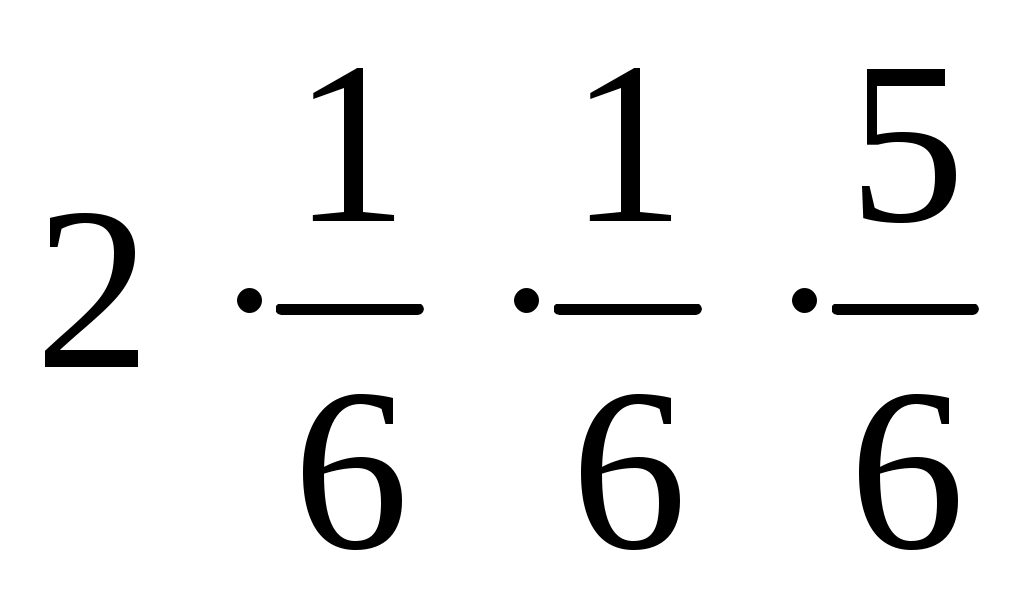 .
. -
Если вероятность выпадения 6 на игральной кости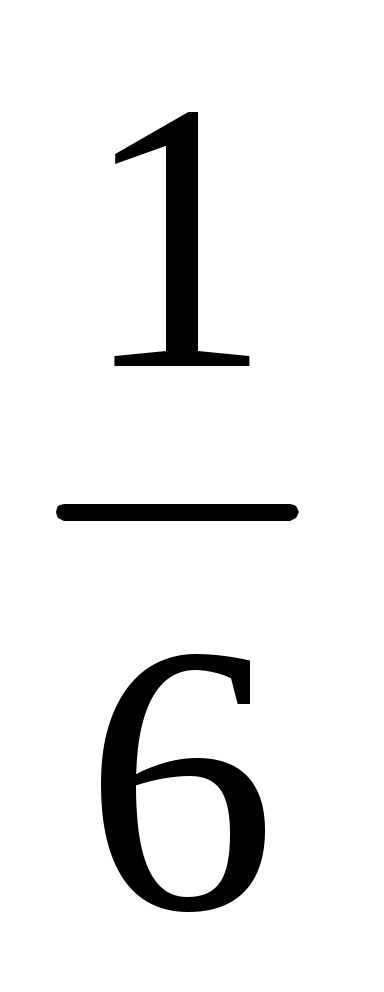 , то наивероятнейшее количество выпадений 6 при 7 бросках равно
, то наивероятнейшее количество выпадений 6 при 7 бросках равно 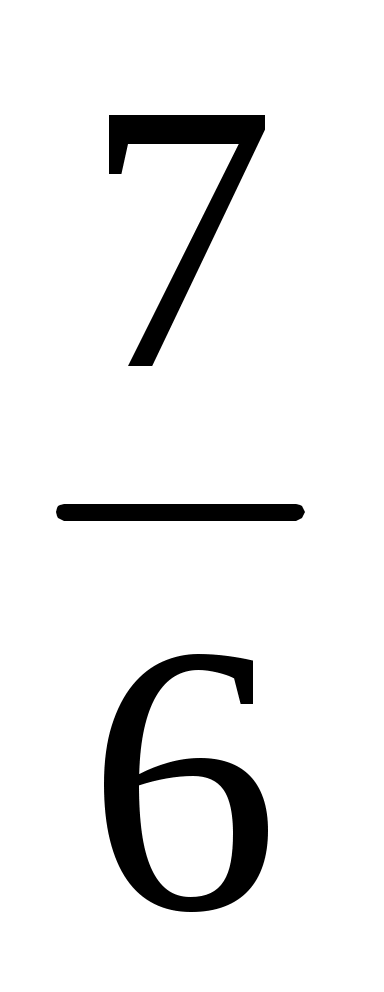 .
. -
Если вероятность выпадения 6 на игральной кости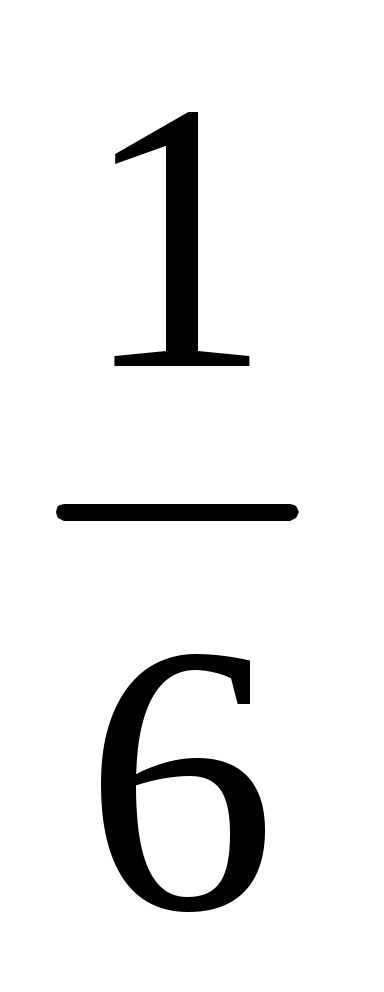 , то наивероятнейшее количество выпадений 6 при 7 бросках равно 1 .
, то наивероятнейшее количество выпадений 6 при 7 бросках равно 1 . -
Если вероятность выпадения 6 на игральной кости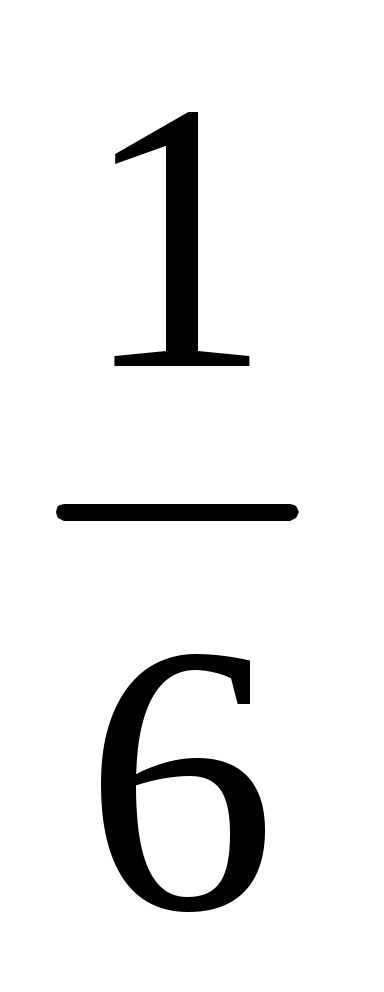 , то наивероятнейшее количество выпадений 6 при 7 бросках равно 2.
, то наивероятнейшее количество выпадений 6 при 7 бросках равно 2. -
Если вероятность выпадения 6 на игральной кости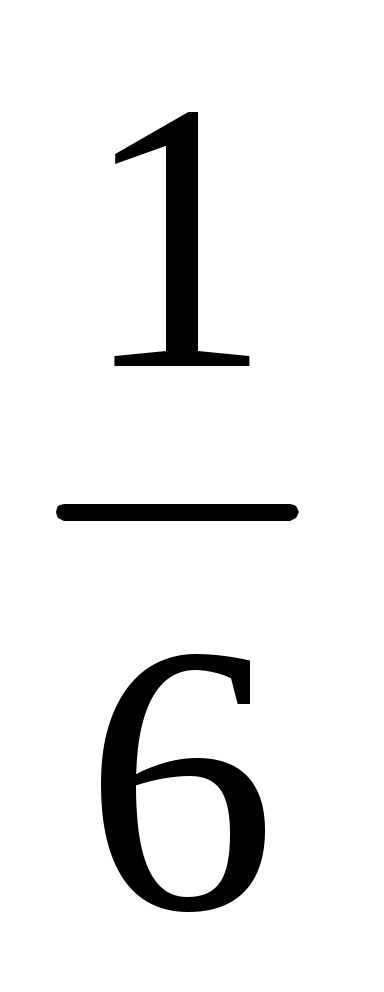 , то математическое ожидание количества выпадений 6 при 7 бросках
, то математическое ожидание количества выпадений 6 при 7 бросках
равно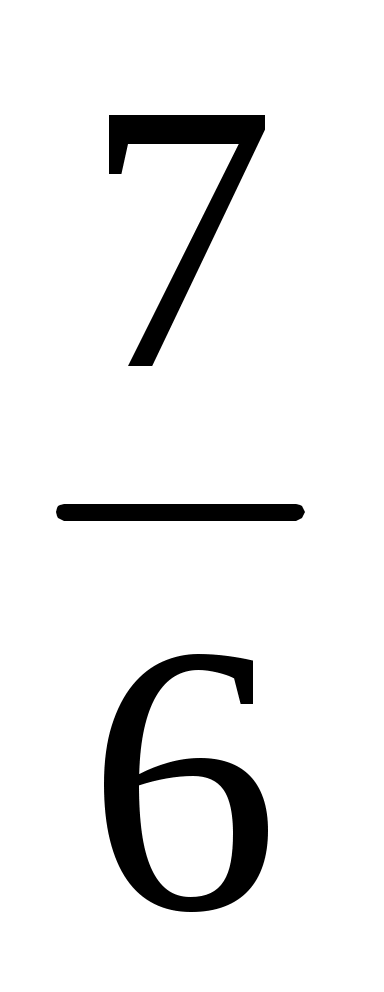 .
. -
Если вероятность выпадения 6 на игральной кости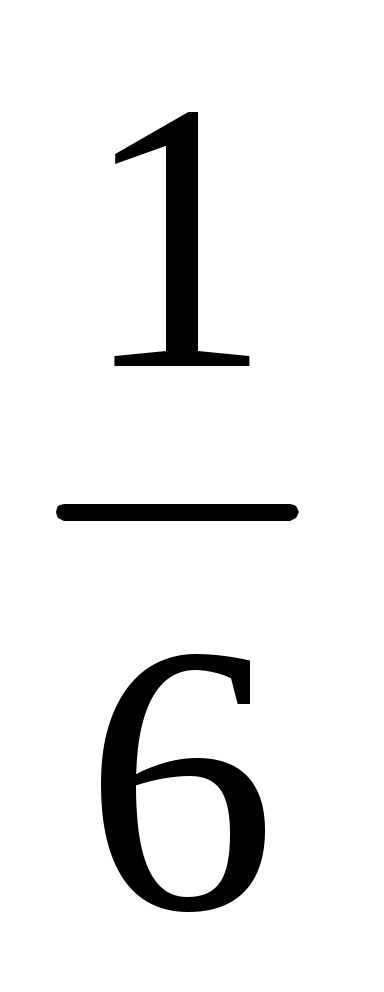 , то математическое ожидание количества выпадений 6 при 7 бросках равно
, то математическое ожидание количества выпадений 6 при 7 бросках равно 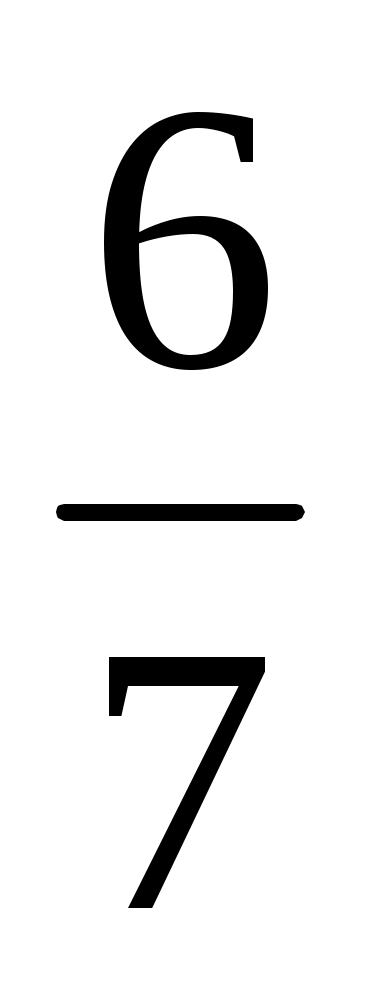 .
. -
Медиана всякой случайной величины обязательно совпадает с ее математическим ожиданием. -
Математическое ожидание случайной величины всегда положительно. -
Для равномерного распределения плотность распределения является постоянной величиной на отрезке. -
Интегральная функция любой случайной величины не убывает. -
Дисперсия любой случайной величины всегда меньше ее математического ожидания. -
Дисперсия любой случайной величины всегда больше ее математического ожидания. -
Плотность вероятности не определена для дискретной случайной величины. -
Вероятность события, которое наверняка произойдёт, равна 1. -
Если Х и Y - любые случайные величины, то D(Х - 2Y)=D(Х) - 4D(Y). -
Для двух совместных событий А и В Р(А+В)=Р(А)+Р(В) – Р(АВ). -
Математическое ожидание случайной величины всегда положительно. -
Условная вероятность Р(А/А)=1. -
Условная вероятность Р(А/А)=0. -
Для равномерного распределения плотность распределения является постоянной величиной на всей числовой оси. -
Если Х и Y- любые случайные величины, то Е(Х+Y)=Е(Х)+Е(Y).
1>
Часть вторая
Простейшие задачи на
непосредственное вычисление вероятности события,
применение формул комбинаторики
-
Игральная кость бросается два раза. Какова вероятность того, что оба раза выпадет одинаковое количество очков. -
Игральная кость бросается три раза. Найти вероятность того, что на верхней грани в первый раз выпадет пять очков, второй раз 6 очков, а третий раз два очка. -
В урне 4 белых и 3 черных шара. Из урны сразу вынимаются два шара. Найти вероятность того, что шары будут разных цветов. -
Какова вероятность, вытягивая из колоды в 36 карт 4 карты, вытянуть 2 дамы и два туза? -
На трех карточках помещены буквы «Г», «О», «Д». Карточки перемешаны и случайным образом подкладываются одна к другой. Какова вероятность, что получится слово «ГОД». -
На пяти карточках напечатана одна из следующих букв: п,о,р,т,с. Вынимая последовательно из ящика карточки наугад и выкладывая их в одну линию, можно получить слово «СПОРТ». Какова вероятность этого события? -
Пять человек случайным образом рассаживаются за круглым столом, среди них Оля и Петя. Найти вероятность того, что Оля и Петя будут сидеть рядом.
Простейшие задачи на геометрическую вероятность
-
В квадрат вписан равнобедренный треугольник так, что его основание совпадает со стороной квадрата. В квадрат случайным образом бросается точка. Найти вероятность того, что точка не попадет в треугольник. -
На плоскость нанесена система параллельных линий, расположенных на расстоянии 3 см друг от друга. На плоскость случайным образом брошена монета диаметром 1 см . Какова вероятность того, что монета не пересечет ни одну из линий?
Простейшие задачи на применение основных свойств вероятностей
-
Два охотника независимо друг от друга стреляют в одну и ту же утку. Вероятность попадания в утку одного из них равна 0.6, а другого 0.7. Найти вероятность попадания в утку. -
Событие А происходит с вероятность0.6. Событие Б происходит с вероятностью 0.7. Предполагается, что оба события независимы.
Чему равна вероятность того, что произойдут оба события -
Событие А происходит с вероятность0.6. Событие Б происходит с вероятностью 0.7. Предполагается, что оба события независимы.
Чему равна вероятность того, что произойдет только первое событие. -
Событие А происходит с вероятность0.6. Событие Б происходит с вероятностью 0.7. Предполагается, что оба события независимы.
Чему равна вероятность того, что произойдет хотя бы одно событие. -
Событие А происходит с вероятность0.6. Событие Б происходит с вероятностью 0.7. Предполагается, что оба события независимы.
Чему равна вероятность того, что события не произойдут. -
Вероятность того, что потребитель увидит рекламу определенного продукта в каталоге, равна 0.04. Вероятность того, что потребитель увидит рекламу того же продукта на рекламном стенде, равна 0.06. Предполагается, что оба события независимы. Чему равна вероятность того, что потребитель увидит обе рекламы? -
Вероятность того, что потребитель увидит рекламу определенного продукта в каталоге, равна 0.04. Вероятность того, что потребитель увидит рекламу того же продукта на рекламном стенде, равна 0.06. Предполагается, что оба события независимы. Чему равна вероятность того, что потребитель увидит хотя бы одну рекламу? -
Вероятность того, что потребитель увидит рекламу определенного продукта в каталоге, равна 0.04. Вероятность того, что потребитель увидит рекламу того же продукта на рекламном стенде, равна 0.06. Предполагается, что оба события независимы. Чему равна вероятность того, что потребитель увидит только рекламу в каталоге? -
Вероятность того, что потребитель увидит рекламу определенного продукта в каталоге, равна 0.04. Вероятность того что потребитель увидит рекламу того же продукта на рекламном стенде, равна 0.06. Предполагается, что оба события независимы. Чему равна вероятность того, что потребитель не увидит рекламы этого товара?
Простейшие задачи на основные распределения случайных величин.
-
Производится серия независимых одинаковых испытаний. В каждом испытании вероятность появления события А одинакова и равна 0.7. Найти вероятность того, что в десяти испытаниях событие А возникнет три раза. -
Случайная величина имеет нормальное распределение с математическим ожиданием 1.7 и средним квадратическим отклонением 4. Какова вероятность попадания такой случайной величины в интервал (1; 2)? Показать математическое ожидание и полученную вероятность на графике плотности нормального распределения. -
Пусть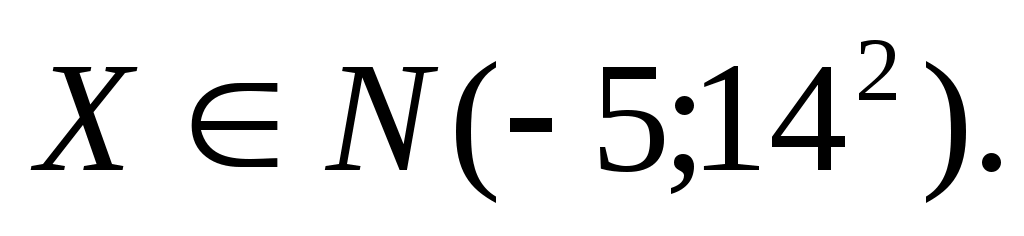 . Найти вероятность попадания
. Найти вероятность попадания 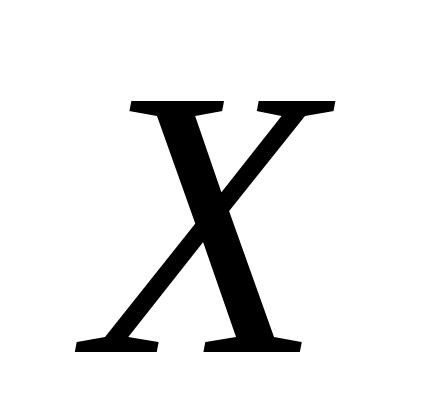 в промежуток
в промежуток 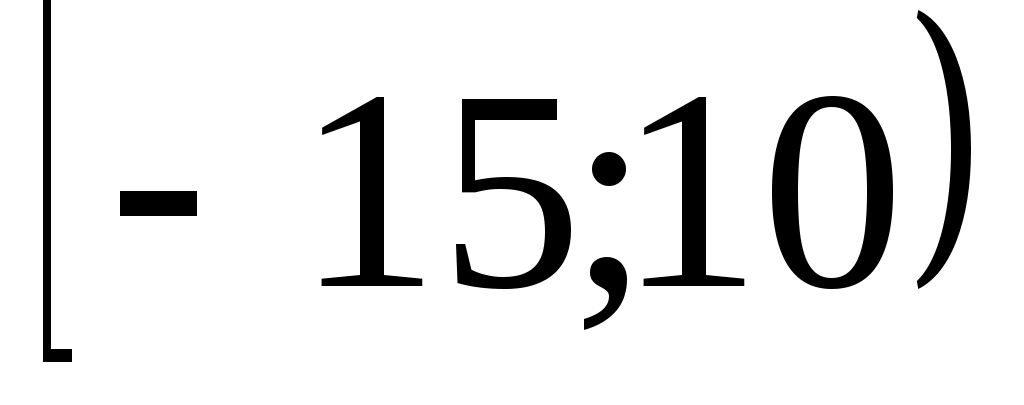 . Построить график плотности заданного нормального распределения и указать на нем фигуру, соответствующую заданной вероятности.
. Построить график плотности заданного нормального распределения и указать на нем фигуру, соответствующую заданной вероятности. -
Случайная величина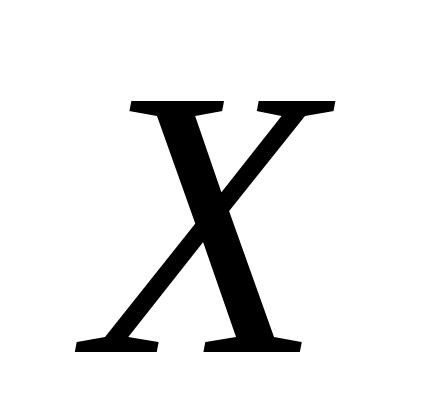 имеет равномерное распределение на отрезке
имеет равномерное распределение на отрезке
[-3:4]. Найти вероятность попадания этой случайной величины в промежуток (-2; 2). Построить график плотности этого распределения и указать на нем фигуру, соответствующую вычисленной вероятности. Найти математическое ожидание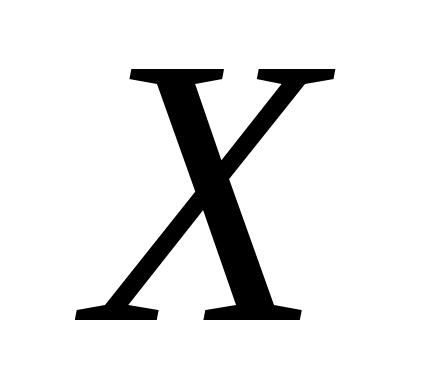 и показать его на графике.
и показать его на графике. -
Случайная величина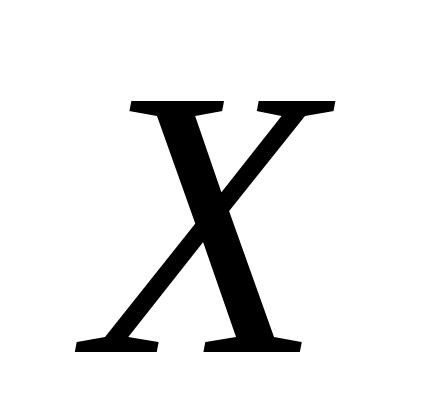 имеет показательной распределение с параметром
имеет показательной распределение с параметром 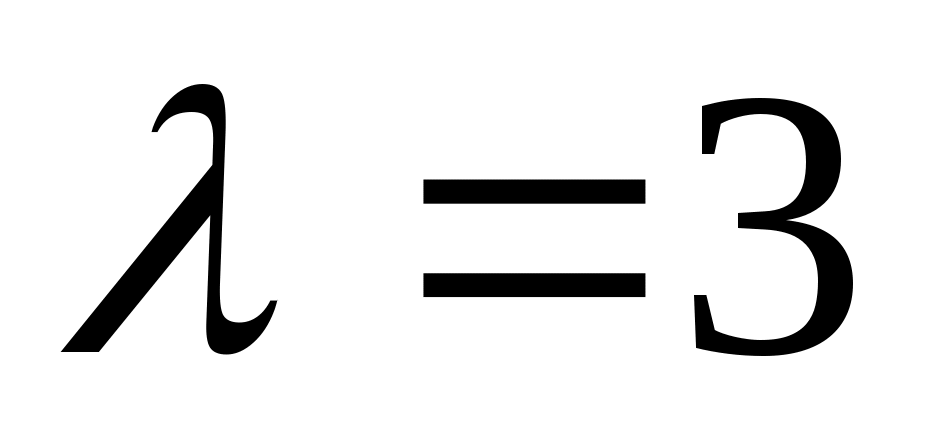 . Найти вероятность попадания этой случайной величины в промежуток (0; +
. Найти вероятность попадания этой случайной величины в промежуток (0; + ). Построить график плотности этого распределения и указать на нем фигуру, соответствующую найденной вероятности. Найти математическое ожидание
). Построить график плотности этого распределения и указать на нем фигуру, соответствующую найденной вероятности. Найти математическое ожидание 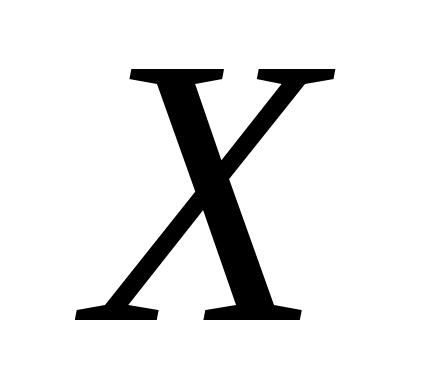 и показать его на графике.
и показать его на графике. -
Случайная величина подчинена закону распределения Пуассона, причем интенсивность потока событий равна 7 событий за единицу времени. Найти вероятность того, что за единицу времени произойдет ровно 5 событий. -
Имеется простейший поток событий, в котором время между двумя соседними событиями подчиняется экспоненциальному закону распределения. Найти вероятность того, что между двумя последовательными событиями пройдет менее 0.2 единиц времени, если интенсивность потока событий равна 7 событий за единицу времени. -
Случайная величина Х распределена по нормальному закону с параметрами m=10 и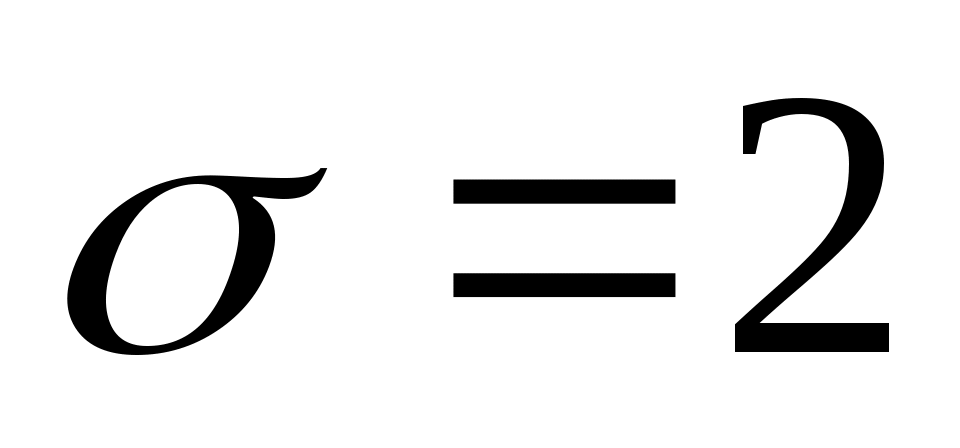 . Найти вероятность попадания Х в промежуток [6;12]. Построить график плотности заданного нормального распределения и указать на нем фигуру, соответствующую найденной вероятности.
. Найти вероятность попадания Х в промежуток [6;12]. Построить график плотности заданного нормального распределения и указать на нем фигуру, соответствующую найденной вероятности. -
Случайная величина имеет равномерное распределение на интервале (5;7). Найти вероятность попадания Х в промежуток [5.5; 6]. Построить график плотности заданного равномерного распределения и указать на нем фигуру, соответствующую найденной вероятности. Вычислить математическое ожидание данной случайной величины и показать его на графике. -
Производится серия независимых испытаний. В каждом испытании вероятность появления события А одинакова и равна 0.4. Найти вероятность того, что в восьми испытаниях событие А возникнет шесть раз. -
Случайная величина имеет нормальное распределение с математическим ожиданием 3 и средним квадратическим отклонением 5. Какова вероятность попадания такой случайной величины в интервал (2; 9)? Показать математическое ожидание и вычисленную вероятность на графике плотности нормального распределения. -
Случайная величина подчинена закону распределения Пуассона, причем интенсивность потока событий равна 6.3 событий за единицу времени. Найти вероятность того, что за единицу времени произойдет ровно 5 событий. -
Имеется простейший поток событий, в котором время между двумя соседними событиями подчиняется экспоненциальному закону распределения. Найти вероятность того, что между двумя последовательными событиями пройдет не менее чем 0.1 единиц времени, если интенсивность потока событий равна 6.3 событий за единицу времени.
Числовые характеристики случайных величин – математическое ожидание, дисперсия и среднее квадратическое отклонение
-
Случайная величина имеет равномерное распределение на отрезке
[0; 1]. Чему равны математическое ожидание и среднее квадратическое отклонение такой случайной величины? -
Случайная величина подчинена закону распределения Пуассона с интенсивностью потока событий, равному 3 событиям за час. Чему равны математическое ожидание и среднее квадратическое отклонение такой случайной величины? -
Случайная величина подчинена показательному (экспоненциальному) закону распределения с интенсивностью потока событий, равному 7 событий за год. Чему равны математическое ожидание и среднее квадратическое отклонение такой случайной величины? -
Непрерывная случайная величина подчинена закону распределения, плотность вероятности которого описывается формулой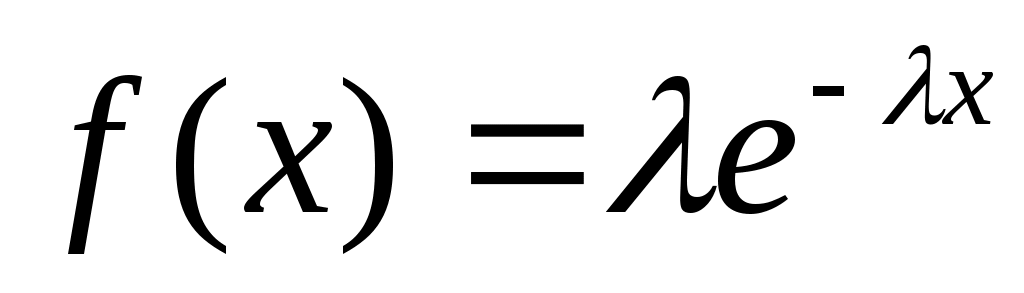 , если переменная x–величина положительная и плотность равна нулю, если переменная x – величина отрицательная. Чему равны математическое ожидание и среднее квадратическое отклонение такой случайной величины?
, если переменная x–величина положительная и плотность равна нулю, если переменная x – величина отрицательная. Чему равны математическое ожидание и среднее квадратическое отклонение такой случайной величины? -
Имеются две независимые случайные величины Х и Y с известными числовыми характеристиками: математические ожидания равны, соответственно, (-5) и 3, а дисперсии 4 и 9. Найти математическое ожидание и среднее квадратическое отклонение случайной величины Z=X-3Y.
Часть третья
Задачи на непосредственное вычисление вероятности события или
применение формул комбинаторики
-
На пяти карточках написаны буквы «П», «П», «О», «О», «Т». Найти вероятность того. Что при случайном выкладывании карточек друг за другом получится слово «ПОТОП». -
Среди кандидатов в студенческий совет факультета 4 первокурсника, 7 второкурсников и 7 третьекурсников. В совет наудачу выбирают 7 человек. Какова вероятность того, что будут выбраны одни третьекурсники? -
Среди кандидатов в студенческий совет факультета 4 первокурсника, 7 второкурсников и 7 третьекурсников. В совет наудачу выбирают 7 человек. Какова вероятность того, что будут выбраны 2 первокурсника и 3 третьекурсника? -
В ящике жетоны с номерами от 1 до 100. Какова вероятность, что первый вынутый жетон не содержит цифру 5?
Задачи на геометрическую вероятность
-
На плоскость с нанесенной сеткой квадратов со стороной 5см наудачу брошена монета радиуса 2см. Найти вероятность того, что монета не пересечет ни одной из сторон квадрата. -
Задача о встрече.
Два друга договорились о встрече в стандартном для них месте "завтра где-то между 13 и 14 часами". Каждый из них прибыл на назначенное место в случайный момент времени из установленного интервала. Будучи "занятыми людьми", они не могли позволить себе ожидать другого более 10 минут. Однако считали за честь ожидать друга "максимально возможное время". Какова вероятность того, что встреча друзей состоялась?