Файл: Учебное пособие для вузов Дружининская И. М. Хованская И. А. Матвеев В. Ф. Мышкис П. А.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 05.12.2023

Просмотров: 259

Скачиваний: 3

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Задачи на показательный закон распределения

  1. Замечено, что посетители офиса данной фирмы образуют пуассоновский поток. Подсчитано, что в среднем приходят 4 человека в час. Найти вероятность того, что: а) за час никто не придет, б) в течение получаса придут 3 человека; в) за 45 минут придут более двух человек.

  2. В банке оператор тратит на обслуживание одного клиента в среднем 20 минут. Какова вероятность того, что: а) за один час оператор обслужит два клиента; б) менее двух клиентов?

  3. Случайная величина имеет показательной распределение с параметром 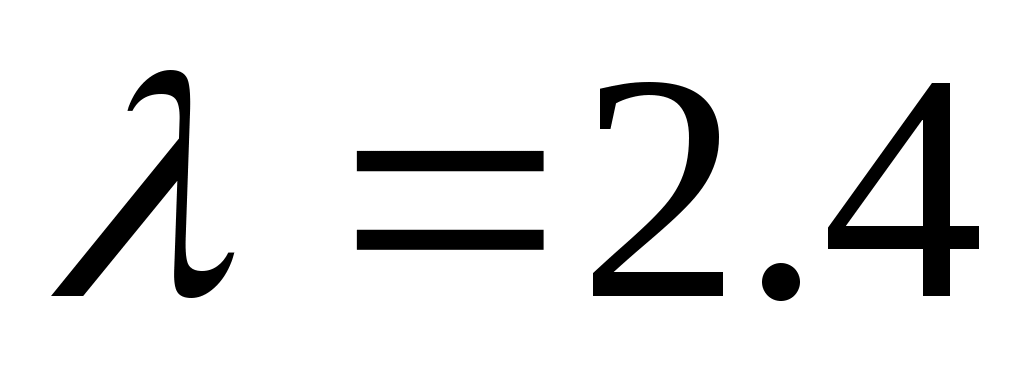. Найти вероятность попадания этой случайной величины в промежуток (-1.5; 3.2). Построить график плотности этого распределения и указать на нем фигуру, соответствующую найденной вероятности. Найти математическое ожидание и показать его на графике. Найти дисперсию и среднее квадратическое отклонение этой случайной величины.

  4. Непрерывная случайная величина имеет плотность распределения следующего вида: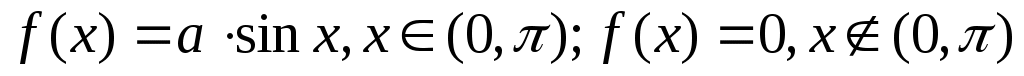 . Найти неизвестный параметр распределения. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение. Показать на графике плотности значения математического ожидания и среднего квадратического отклонения. Найти вероятность попадания значений случайной величины в интервал 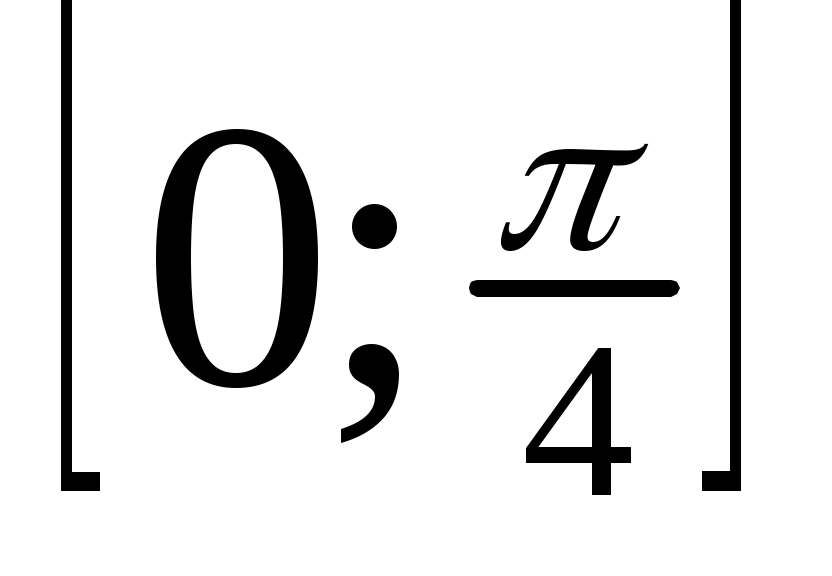; показать на графике эту вероятность.

  5. Получить ряд распределения для случайной величины – числа попаданий в цель при двух выстрелах, если вероятность попадания в цель равна 0.8 при одном выстреле. Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение этой случайной величины. Построить график функции распределения и показать на нем математическое ожидание и среднее квадратическое отклонение.

Числовые характеристики случайных величин и их свойства

  1. Имеются две независимых случайных величины и 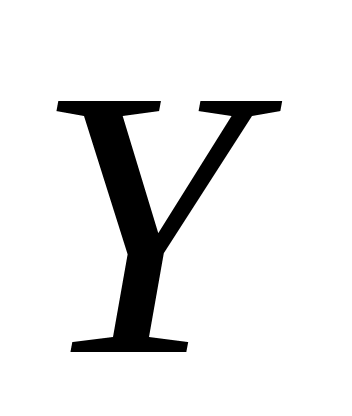с известными математическим ожиданием и дисперсией: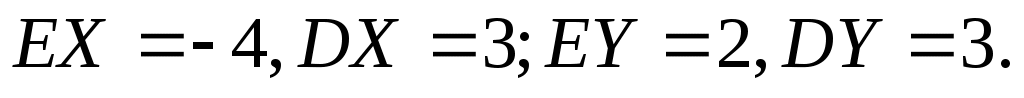

Найти математическое ожидание и дисперсию случайной величины .

  1. Коэффициент корреляции между случайными величинами и равен 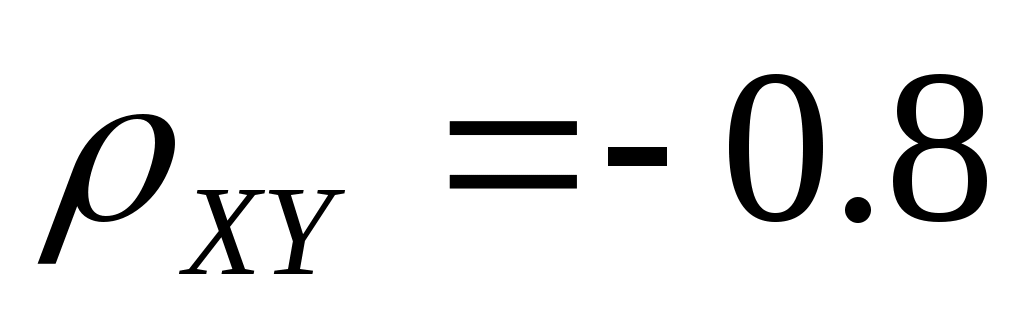. Найдите коэффициент корреляции 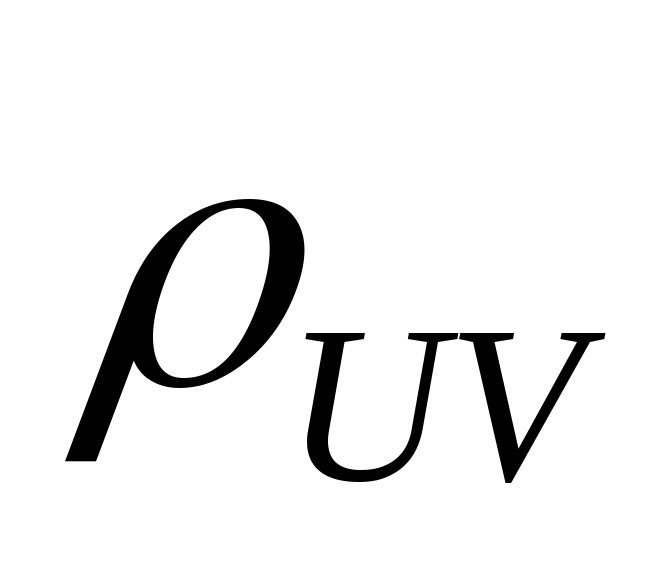между случайными величинами 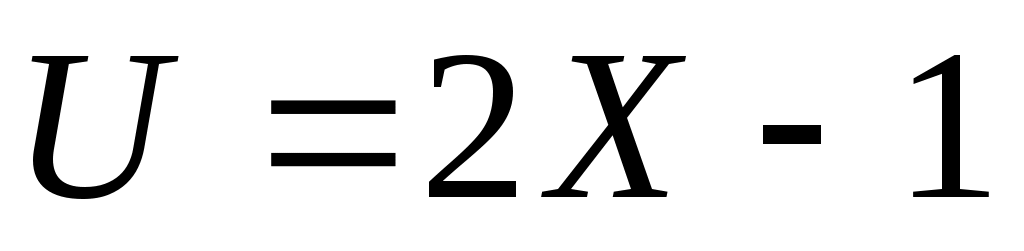и .

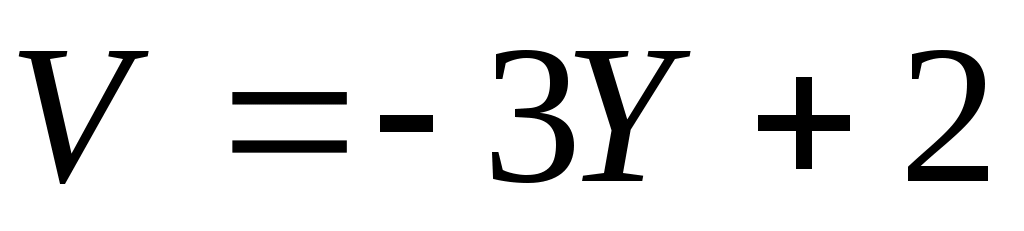  2. Имеются три независимые случайные величины X, Y, Z с известными математическими ожиданиями, которые, соответственно, равны (-5), (-2) и 3. Найти математические ожидания двух других случайных величин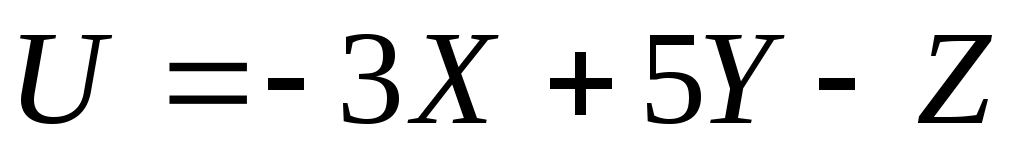 и .

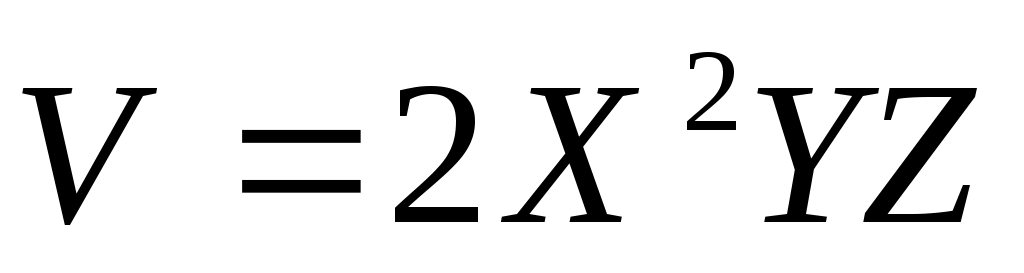  3. Доход фирмы за месяц представляется нормально распределенной случайной величиной со средним значением 3 млн. долл. и средним квадратическим отклонением 0.5 млн. долл. . Найдите вероятность того, что в данном месяце доход фирмы будет более 4 млн. долл. Напишите формулу плотности распределения этой случайной величины, нарисуйте ее график и покажите на нем вычисленную вероятность.

  4. Доход фирмы за месяц представляется нормально распределенной случайной величиной со средним квадратическим отклонением 0.5 млн. долл. Известно, что в 70% случаев доход фирмы превышает 4 млн. долл. Найдите средний доход фирмы.

  5. Минутная стрелка электрических часов перемещается скачком в конце каждой минуты. Найти вероятность того, что в данное мгновение часы покажут время, которое отличается от истинного более чем на 20 секунд.

Зависимые и независимые случайные величины

  1. Сотрудник фирмы, отвечающий на телефонные звонки, получает много обращений по разным вопросам. В 75% случаев лишь запрашивается информация, в то время как 15% звонков связаны с реальными заказами. Кроме того, в 10% случаев запрашивается информация и делается заказ.
    а) Являются ли события – «запрашивается информация» и «делается заказ» – зависимыми? б) Найдите условную вероятность того, что некоторый звонок не связан с обращением за информацией при условии, что в результате звонка делается заказ.

Часть четвертая

(задачи повышенной сложности)

  1. Имеется инвестиционный портфель, который стоит из трех видов ценных бумаг. Доли вложения капитала в эти ценные бумаги относятся как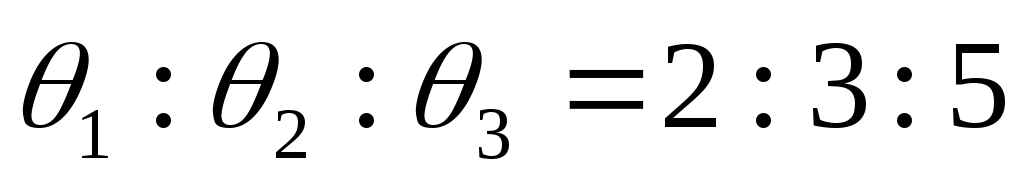 , причем 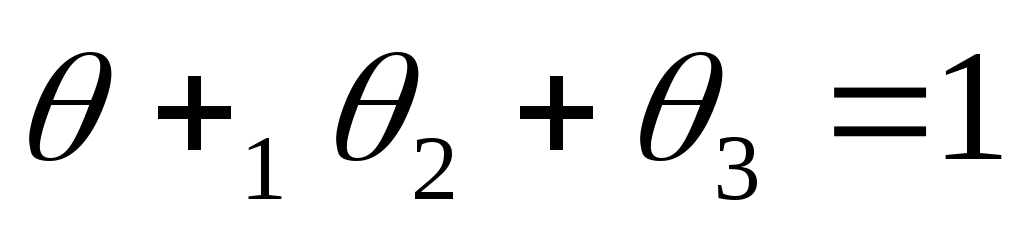. Известно, что нормы прибыли по каждому виду ценных бумаг есть нормально распределенные случайные величины, причем их можно считать независимыми. Средние нормы прибыли по каждому виду ценных бумаг таковы (в процентах): 10, 8, 12; их абсолютные уровни риска (средние квадратические отклонения) таковы (процентах): 3, 1, 4. Найти среднюю норму прибыли всего портфеля и его уровень риска. Найти вероятность того, что норма прибыли по всему портфелю окажется более 12%.

  2. На новогодней елочке висит гирлянда из 10 последовательно соединенных разноцветных лампочек. Промежутки времени до отказа каждой из них являются независимыми, показательно распределенными случайными величинами с одинаковой интенсивностью потока событий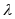 =0.01, при этом время измеряется в часах. Найти среднее время работы гирлянды.

  3. Новый служащий поступил на работу в некоторое агентство и дожидается первого клиента. Время ожидания имеет показательное распределение с параметром l=1 (посещений за час). Если клиент не заинтересован сервисом агентства (такое случается с вероятностью 1/3), то на разговор с ним уйдёт 6 минут, если клиент сделает небольшой заказ (вероятность такого события 1/2), служащий потратит на него 30 мин, если клиент сделает крупный заказ (с вероятностью 1/6), то разговор займёт 1 час. После общения с первым клиентом служащий должен позвонить начальнику. Найти математическое ожидание времени, прошедшего с начала работы нового служащего до звонка начальнику.

  4. Наудачу выбрано натуральное число, не превосходящее 20. Пусть Х - число натуральных делителей выбранного числа. Найдите закон распределения случайной величины Х. (Единица и само число рассматриваются в качестве делителей).

  5. Партия «Тыблоко» выдвигает трех кандидатов А, Б и В в Думу города Торонто. Шансы кандидатов быть избранными специалисты оценивают как 0.2; 0.4 и 0.5, соответственно. По предварительным подсчётам стало известно, что 2 кандидата партии прошли в Думу. Найти вероятность того, что среди них есть кандидат В.

  6. Для надежности схемы устанавливается n параллельно соединенных и независимо работающих элементов, причем промежутки времени работы каждого элемента до отказа распределены по показательному закону с интенсивностью потока событий 0.05 отказа за час. Сколько нужно поставить таких элементов (найти n), чтобы с вероятностью 0.99 схема безотказно работала в течение 10 часов?

  7. Три охотника стреляют в медведя. Первый из них попадает в медведя с вероятностью 0.7, второй - 0.8, третий – 0.6. Медведь убит, в нём оказалось 2 пули. Найти вероятность того, что второй охотник не попал.

  8. Опыт состоит в делении заданного отрезка случайным образом на три части. Предположим, что производится 6 независимых опытов такого рода. Какова вероятность того, что в двух опытах: из полученных частей можно составить треугольник?

  9. Магазин мобильных телефонов посещает в среднем 7 человек в час. Каждому посетителю магазин дарит ручку с фирменным логотипом. Кроме того, каждый час разыгрывается рекламная лотерея, приз в которой (мобильный телефон) вручается одному из игроков с вероятностью 1/20. Рабочий день длится 10 часов. Найти математическое ожидание стоимости призов, требующихся этому магазину на один день, если ручка стоит 30 рублей, а мобильный телефон 7 000 рублей.

  10. Экспериментатор подбрасывает игральную кость и монетку. Если выпадает орёл, то количество очков, выпавших на кубике, увеличивается на 2, если решка, то количество очков, выпавших на кубике, остаётся неизменным. Найти математическое ожидание и дисперсию количества полученных очков.


Образец варианта
экзаменационной контрольной работы

Первая часть

(каждый вопрос требует ответа: «ДА» или «НЕТ»)

  1. Вероятность события, которое не может произойти, не существует.

  2. Медиана всякой случайной величины обязательно совпадает с ее математическим ожиданием.

  3. . Если Х и Y- любые независимые случайные величины, a и b любые числа, то D(aХ +bY)=aD(Х)+bD(Y).

  4. Случайная величина, распределенная по закону Пуассона, не может принять значение, равное трем.

Вторая часть

(в этой части «вес» каждой задачи равен 1 баллу)

  1. Производится серия независимых испытаний. В каждом испытании вероятность появления события А одинакова и равна 0.3. Найти вероятность того, что в семи испытаниях событие А возникнет четыре раза.

  2. Случайная величина имеет нормальное распределение с математическим ожиданием (-1) и средним квадратическим отклонением 3. Какова вероятность попадания такой случайной величины в интервал (-2; 1)? Показать математическое ожидание и вычисленную вероятность на графике плотности нормального распределения.

  3. Случайная величина подчинена закону распределения Пуассона, причем интенсивность потока событий равна 2 события за единицу времени. Найти вероятность того, что за единицу времени произойдет ровно 4 события.

  4. Имеется простейший поток событий, в котором время между двумя соседними событиями подчиняется экспоненциальному закону распределения. Найти вероятность того, что между двумя последовательными событиями пройдет более 0.8 единиц времени, если интенсивность потока событий такая же, как в предыдущей задаче.

Третья часть

(в этой части «вес» каждой задачи указан в квадратных скобках)

9. [0.5] Вероятность получить высокие дивиденды по акциям на первом предприятии - 0.1, на втором - 0.2, на третьем – 0.25. Определить вероятность того, что акционер, имеющий акции всех предприятий, получит высокие дивиденды: а) на всех предприятиях; б) только на одном предприятии; в) хотя бы на одном предприятии.

10. [1] Ежедневная прибыль фирмы «Ой-ой-ой» является случайной величиной с плотностью вероятностей вида

Смотрите также файлы