Файл: Учебнометодическое пособие по выполнению лабораторных работ санктпетербург 2023 удк 621. 39(09)(076) ббк 32. 81я73 к 63.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 144
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
В случае симметричной диафрагмы
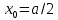 вместо (4.4) имеем
вместо (4.4) имеем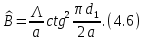
На рис. 4.3,а указаны геометрические параметры диафрагмы, края которой параллельны широким стенкам волновода (
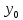 – координата середины отверстия).
– координата середины отверстия). 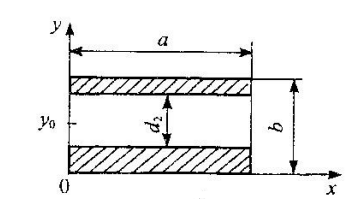 | 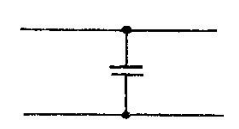 |
| а) | б) |
| Рис. 4.3. Емкостная диафрагма и ее эквивалентная схема. | |
Эквивалентная реактивность такой диафрагмы имеет для волны
 емкостной характер (рис. 4.3,б), вследствие чего эту диафрагму называют емкостной. Ее нормированная проводимость определяется приближенным выражением
емкостной характер (рис. 4.3,б), вследствие чего эту диафрагму называют емкостной. Ее нормированная проводимость определяется приближенным выражением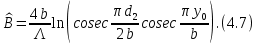
В случае симметричной емкостной диафрагмы
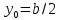 вместо (4.7) получаем
вместо (4.7) получаем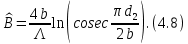
В работе исследуются симметричные диафрагмы.
На рис. 4.4,а изображена диафрагма, которую можно рассматривать как результат совмещения в одном и том же поперечном сечении волновода симметричных индуктивной и емкостной диафрагм. Для волны
 такая диафрагма имеет эквивалентную схему в виде параллельного колебательного контура (рис. 4.4,б)
такая диафрагма имеет эквивалентную схему в виде параллельного колебательного контура (рис. 4.4,б) 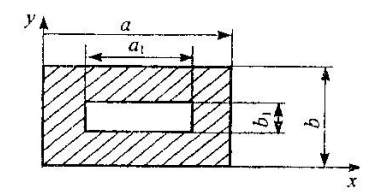 | 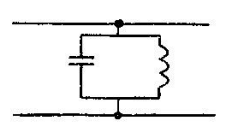 |
| а) | б) |
| Рис. 4.4. Резонансная диафрагма и ее эквивалентная схема. | |
Если размеры
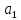 и
и 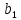
прямоугольного отверстия этой диафрагмы удовлетворяют соотношению
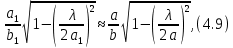
то диафрагма становится резонансной, т.е. ее эквивалентная проводимость оказывается равной нулю. Волна
 частоты
частоты 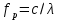 (где
(где  – длина волны, фигурирующая в уравнении (4.9)) проходит через резонансную диафрагму без отражения, так как в этом случае волны, отраженные от эквивалентных индуктивности и емкости (рис. 4.4,б), имеют одинаковые амплитуды и противоположные фазы и компенсируют друг друга. Очевидно, что при заданных
– длина волны, фигурирующая в уравнении (4.9)) проходит через резонансную диафрагму без отражения, так как в этом случае волны, отраженные от эквивалентных индуктивности и емкости (рис. 4.4,б), имеют одинаковые амплитуды и противоположные фазы и компенсируют друг друга. Очевидно, что при заданных  и
и  одно уравнение (4.9) не может определить однозначно два размера
одно уравнение (4.9) не может определить однозначно два размера  и
и  диафрагмы. Согласно (4.9) предельные случаи резонансной диафрагмы таковы:
диафрагмы. Согласно (4.9) предельные случаи резонансной диафрагмы таковы: 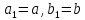 (диафрагма отсутствует) и
(диафрагма отсутствует) и 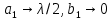 (узкая полуволновая щель).
(узкая полуволновая щель).Порядок выполнения работы
А). Моделирование
1). Создать прямоугольный волновод на основе работ 1,2, сечение волновода
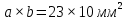 .
.2). С помощью элемента управления Duplicate Along Line создать еще 2 прямоугольных волновода.
3). Добавить симметричный нерегулярный элемент произвольного размера, подходящий под выражения (4.6), (4.8) и (4.10), в каждый из волноводов как на рис. 4.3. Это можно сделать с помощью элемента Subtract.
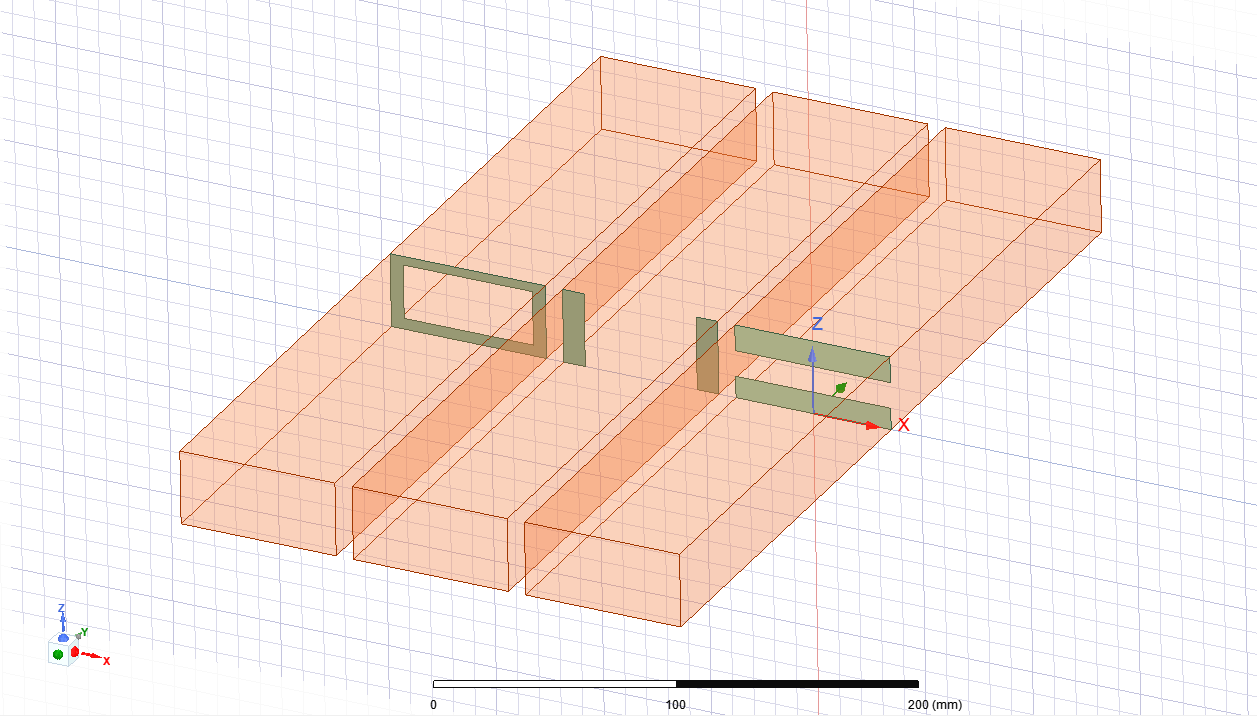 |
| Рис. 4.5. Нерегулярные элементы в волноводе. |
4). Проанализировать поведение волн в волноводе с помощью анимированных полей внутри волноводов. Анализ проводить в диапазоне частот от 9 до 11 ГГц хотя бы 51 точкой на частотной сетке.
5). В окне Project Manager нажать правой кнопкой мыши на элемент Results, Create Modal Solution Data Report, Rectangular Plot.
6). В открывшемся окне выбрать VSWR, далее VSWR (2) и нажать New Report.
7). Повторить операцию для VSWR (4) и VSWR (6).
Б). Расчеты
Для построенных диафрагм рассчитать КСВ по формулам (4.3), (4.5), (4.6), (4.8) и сравнить с полученными в результате моделирования результатами. Свести результат в таблицу 4.1.
| Вид нерегулярного элемента, его геометрические параметры | 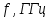 | 9 | 9,5 | 10 | 10,5 | 11 |
| | 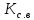 расчет расчет | | | | | |
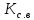 модель модель | | | | | |
Лабораторная работа 5.
Исследование характеристик объемного резонатора
Цель работы
1. Изучение устройства закрытых цилиндрических объемных резонаторов и электромагнитных процессов в них.
2. Освоение методов измерений основных параметров резонатора (резонансной частоты и добротностей).
Методические указания по самоподготовке.
При подготовке к лабораторной работе изучите разделы учебника, посвященные закрытым цилиндрическим объемным резонаторам [1] или [2].
1. При изучении общих свойств закрытых объемных резонаторов (ОР) обратите, прежде всего, внимание на их назначение, на сходство и различие процессов в резонаторах и обычных колебательныхLC-контурах, на определения понятий параметров, которые подлежать измерению: резонансной частоты и добротностей. Разберитесь в характере поля вдоль отрезка линии передачи, короткозамкнутого с обоих концов (стоячая волна), и в условии резонанса (на длине отрезка должно укладываться целое число полуволн). Рассмотрите конструкции закрытых цилиндрических резонаторов: коаксиального (в том числе с укорачивающей емкостью), прямоугольного и круглого. Уясните ориентацию и расположение элементов связи (зонда, петли и отверстия) по отношению к полю рабочего типа колебаний. Заметьте, что ОР может иметь как один, так и два (на входе и выходе) элемента связи; в первом случае он называется непроходным, а во втором – проходным резонатором.
Очень важно понять возможные способы перестройки частоты ОР изменением его длины, внесением в него металлического или диэлектрического тела (винта, шайбы). Естественно, что немного изменяют частоту ОР и элементы связи. В любом случае нарушается установившийся при резонансе баланс электрической и магнитной энергий, который восстанавливается уже на другой резонансной частоте ОР(
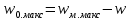 ).
).2. Вблизи резонансной частоты ОР имеет частичную характеристику, подобную параллельному LC-контуру. Поэтому на эквивалентной схеме он условно изображается параллельным соединением
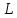 ,
, 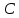 и
и 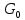 элементов,
элементов, 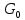 – активная проводимость, которая учитывает потери в резонаторе. Реальными параметрами ОР являются резонансная частота
– активная проводимость, которая учитывает потери в резонаторе. Реальными параметрами ОР являются резонансная частота 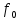 и нагруженная добротность.
и нагруженная добротность.
Как известно, нагруженная (или полная) добротность резонатора
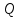 выражается соотношением
выражается соотношением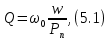
где
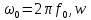 – запасенная при резонансе внутри ОР электромагнитная энергия исследуемого типа колебаний,
– запасенная при резонансе внутри ОР электромагнитная энергия исследуемого типа колебаний, 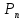 – средняя за период мощность полных потерь. Мощность
– средняя за период мощность полных потерь. Мощность 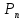 складывается из мощности собственных потерь резонатора
складывается из мощности собственных потерь резонатора 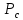 и мощности потерь через элементы связи во внешних цепях
и мощности потерь через элементы связи во внешних цепях 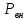 :
: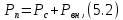
Поэтому можно ввести соответствующие мощностям потерь
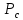 и
и 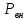 частичные собственную
частичные собственную 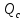 и внешнюю
и внешнюю 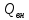 добротности. Из (5.1) и (5.2) легко установить следующую связь между добротностями:
добротности. Из (5.1) и (5.2) легко установить следующую связь между добротностями: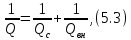
причем
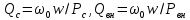 .
.Вспомните, что основным методом измерения параметров контуров является метод четырехполюсника. Он применим и для ОР проходного типа. Как известно, по этому методу снимается зависимость мощности на выходе резонатора от частоты при постоянной входной мощности.
Более характерен для техники СВЧ метод двухполюсника, пригодный как для проходного ОР, так и непроходного. В методе двухполюсника снимается частотная характеристика (ЧХ) коэффициента стоячей волны (КСВ) в волноводе, который нагружен на объемный резонатор. Зависимость КСВ от частоты имеет резонансной частоте
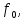 (рис. 5.1). Следует отметить, что поскольку ОР – многорезонансная система, существует ряд резонансных частот, соответствующих различным типам колебаний резонатора.
(рис. 5.1). Следует отметить, что поскольку ОР – многорезонансная система, существует ряд резонансных частот, соответствующих различным типам колебаний резонатора. 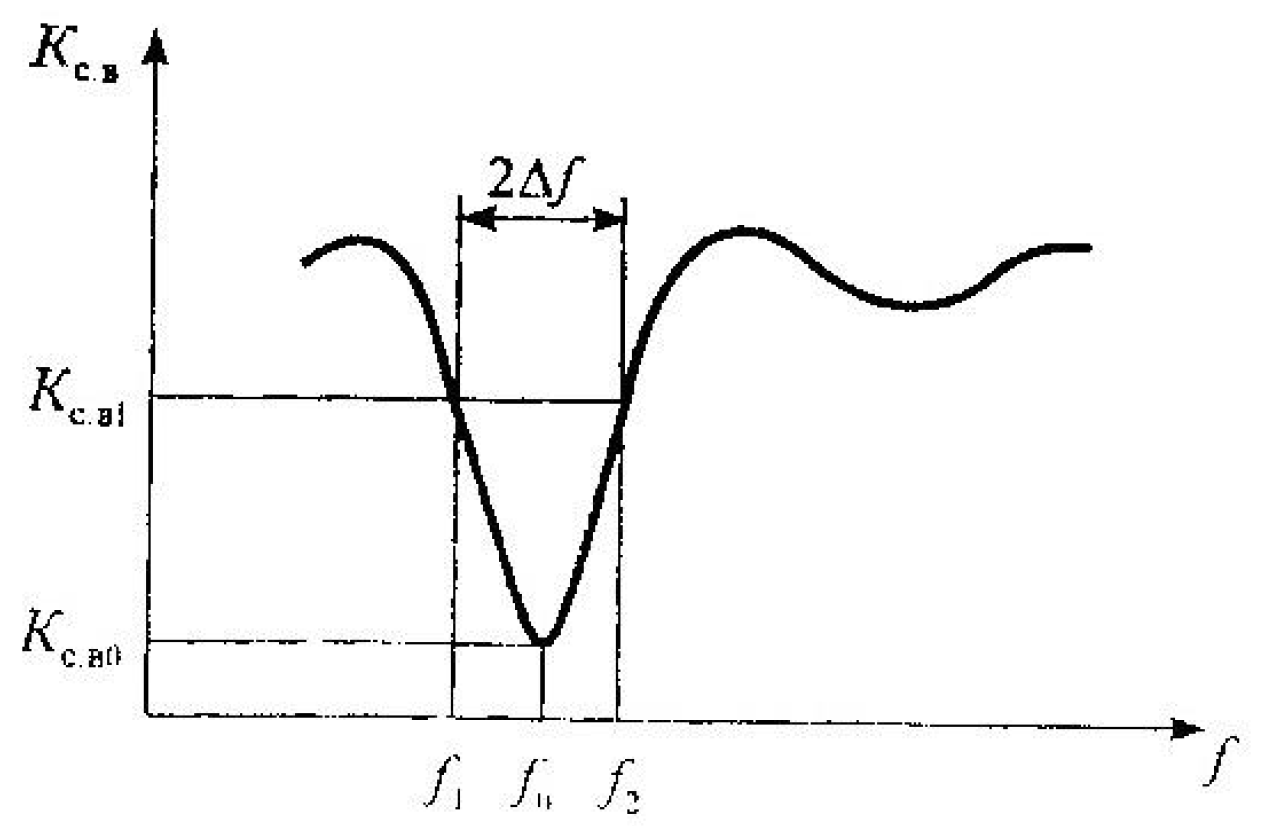 |
| Рис. 5.1. Зависимость КСВ от частоты. |