Файл: Государственное образовательное учреждение высшего профессионального образования волгоградский государственный технический университет.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 60
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
3) расчётного значения критерия Смирнова-Грабса:
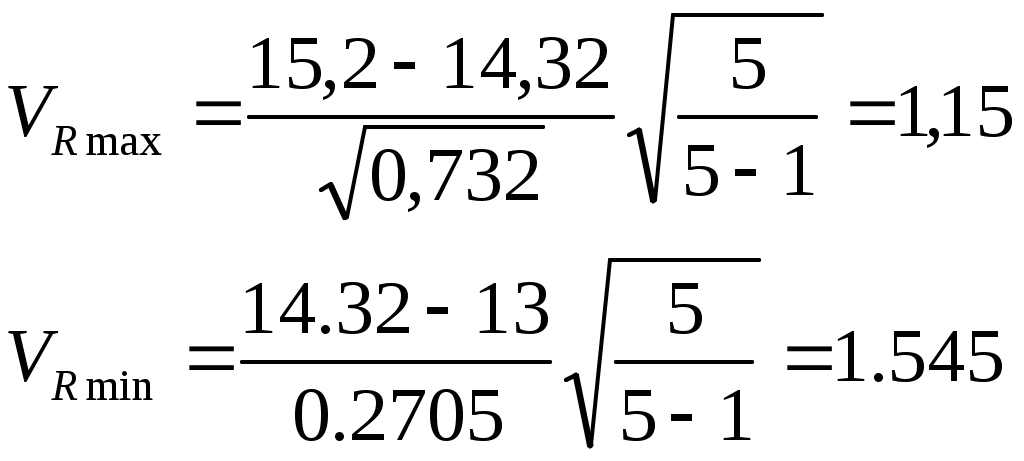
По приложению А находим, что
Вторая операция — проверка гипотезы о нормальном распределении случайных величин Yuv. Проверка этой гипотезы также проводится для каждого опыта матрицы. Рассмотрим эту операцию на примере первого опыта матрицы, при X=2. Проверка включает
1) определение расчетного значения критерия WR по формуле:
| | (1) |
| где | (2) |
Используя приложение Д в рассматриваемом примере находим
Q=0,6646·(15,2–13)+0,2413·(14,8–14)=1,655, поэтому
2) сравнение расчетного значения
(см. приложение Е), которое определяется для заданной доверительной вероятности и известного числа повторных опытов (измерений) m. Для рассматриваемого примера
Так как расчетное значение критерия
В табл. 3 приведены значения WR и для других опытов матрицы. Эти значения также превышают табличные, и поэтому первое условие о возможности применения регрессионного анализа удовлетворяется.
Третья операция – проверка гипотезы об однородности дисперсий в опытах матрицы.
Так как число повторных опытов (m=5) одинаково для всех опытов матрицы, то для проверки однородности дисперсий применяется критерий Кочрена, расчетное значение которого:
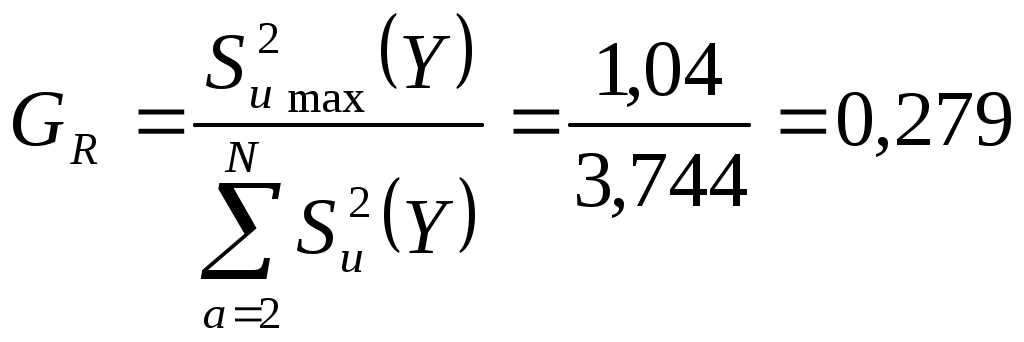 | (3) |
Расчетное значение GR сравнивается с табличным значением GT, которое определяют по приложению Б в зависимости от числа опытов в матрице N и числа степеней свободы дисперсии
Четвертая операция — определение средней дисперсии выходного параметра в опытах матрицы. Если в опытах матрицы дисперсии однородны и число повторных опытов одинаково, то средняя дисперсия определяется по формуле:
| | (4) |
Число степеней свободы этой дисперсии равно:
| | (5) |
Средняя дисперсия характеризует средний разброс значений выходного параметра относительно его средних значений при каждом уровне факторов, т. е. ошибку опытов в эксперименте. В рассматриваемом примере эта дисперсия, или, как ее называют, дисперсия воспроизводимости, равна:
Если число повторных опытов неодинаково при различных уровнях факторов, то для проверки однородности дисперсий используется критерий Бартлета. Если случайные величины Yu не имеют нормального распределения, то применять критерий Бартлета не рекомендуется, так как он получен при условии нормального распределения этих величин.
При неоднородных дисперсиях или переходят к преобразованию значений выходного параметра, чтобы сделать дисперсии однородными, или применяют вариант метода наименьших квадратов с учетом величины дисперсии каждого опыта.
Пятая операция – определение подходящего вида регрессионной модели. Для определения подходящего вида регрессионной модели необходимо определить:
-
вид взаимосвязи Y=f(X), устанавливаемый при теоретическом исследовании объекта или процесса; -
графическую взаимосвязь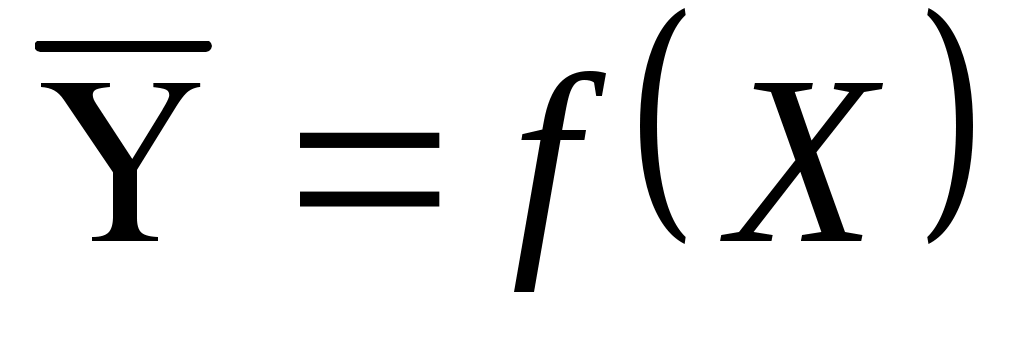 между средними значениями выходного параметра для каждого уровня факторов и значений по данным эксперимента. При сопоставлении этого графика с графиками известных функций устанавливают вид уравнения;
между средними значениями выходного параметра для каждого уровня факторов и значений по данным эксперимента. При сопоставлении этого графика с графиками известных функций устанавливают вид уравнения; -
характер изменения раздельных или нераздельных раздельностей первого порядка, определяемых по данным эксперимента.
Если в результате эксперимента получены следующие пары значений:
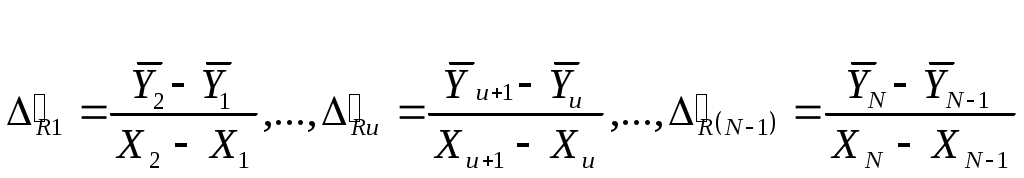
и не разделёнными разностями первого порядка – величины
| | (6) |
Неразделённые разности первого порядка используют, когда интервал варьирования факторов постоянный, т.е.
В рассматриваемом примере интервал варьирования факторов постоянный и равен
Ввиду малого различия неразделенных разностей первого порядка выходного параметра, не превышающего удвоенной величины среднеквадратической ошибки эксперимента (2S(1){Y} = 1,724), можно считать, что они тождественны и поэтому для описания экспериментальных данных можно условно принять уравнение прямой линии:
| | (7) |
| | (8) |
| | (9) |
Использование уравнения (8) позволяет упростить статистические расчёты при обработке экспериментальных данных, так как коэффициенты регрессии а0 и а1 не коррелированны. Коэффициенты регрессии а0 и а1являются оценками истинных коэффициентов регрессии
Шестая операция — определение коэффициентов регрессии. Если дисперсии выходного параметра для каждого уровня фактора однородны, то для определения коэффициентов регрессии в уравнении можно применять метод наименьших квадратов. Используя условие
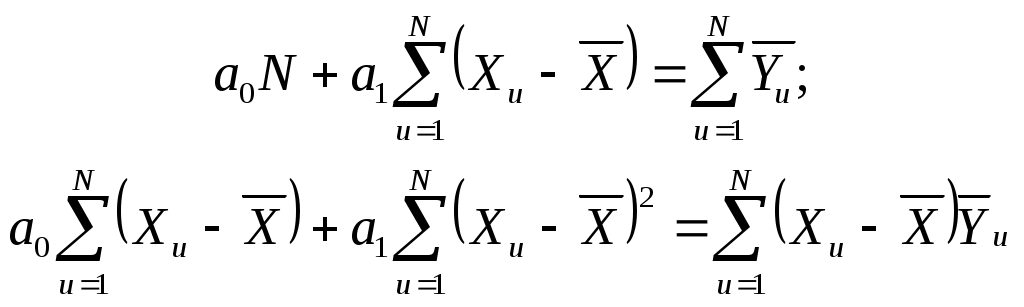 | (10) |
Так как
| | (11) | 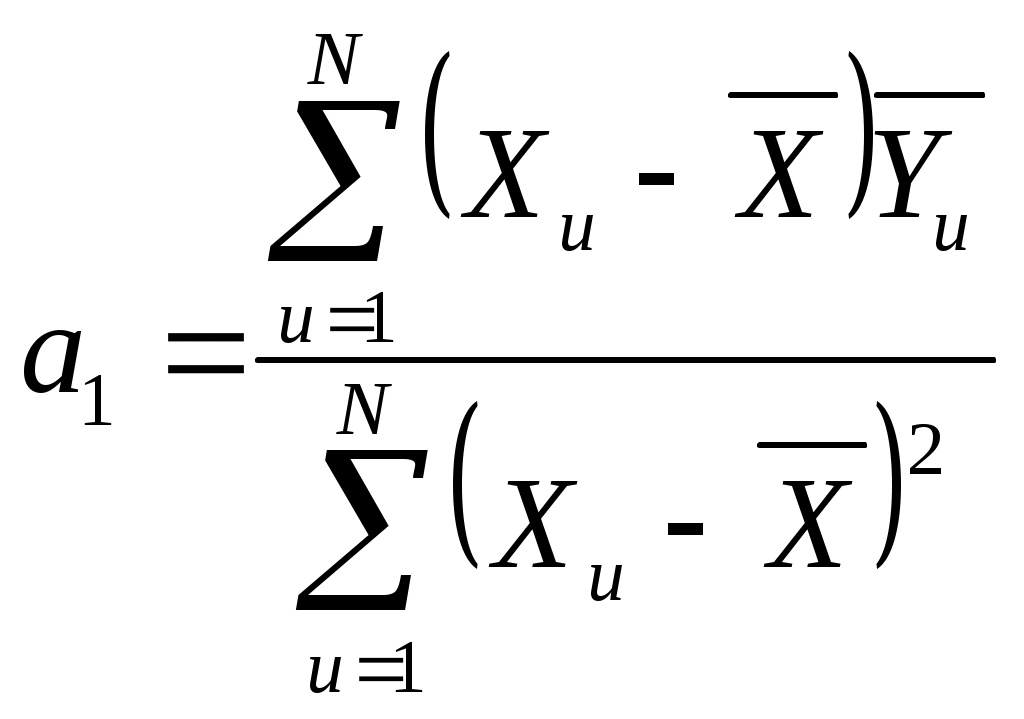 | (12) |