Определим по формулам (11) и (12) коэффициенты регрессии для рассматриваемого примера. Расчеты необходимых сумм сводим в табл. 4.

Таблица 4

u
1 2 3 4 5	2 4 6 8 10	-4 -2 0 2 4	16 4 0 4 16	14,32 21,72 30 37,84 46,32	-57,28 -43,44 0 75,68 185,28
∑	30	0	40	150,20	160,24

По формулам (9), (11), (12) находим:



Поэтому искомое уравнение имеет вид:

(13)

График этой функции изображен на рис. 2.

Седьмая операция – определения адекватности полученного уравнения. Для определения адекватности полученного уравнения используют критерий Фишера, расчетное значение которого определяют по формуле:

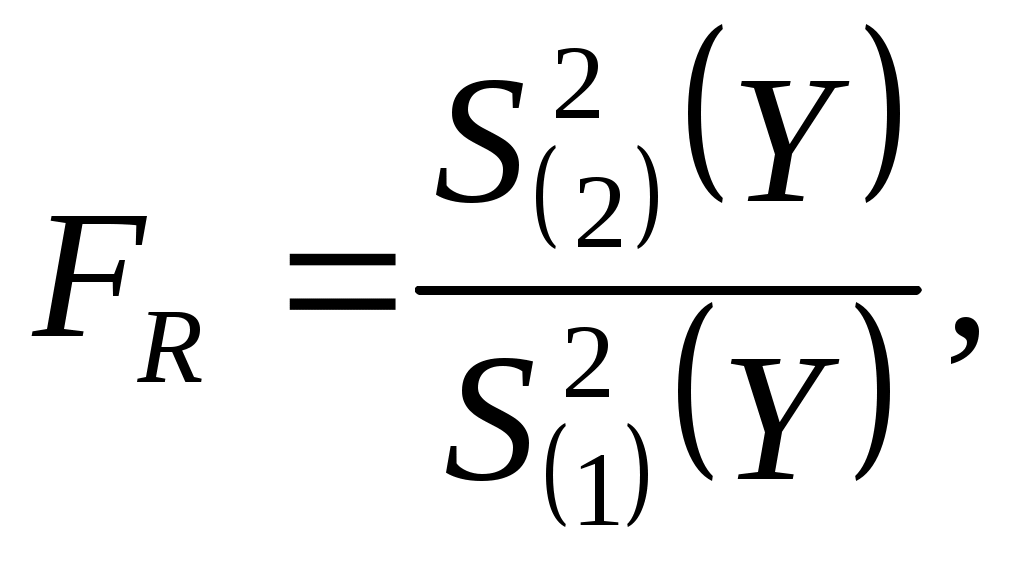(14)

где средняя дисперсия или дисперсия воспроизводимости, определяемая по формуле (4); дисперсия, характеризующая рассеивание средних экспериментальных значений

---

относительно прямой линии, определяемой по формуле (8).

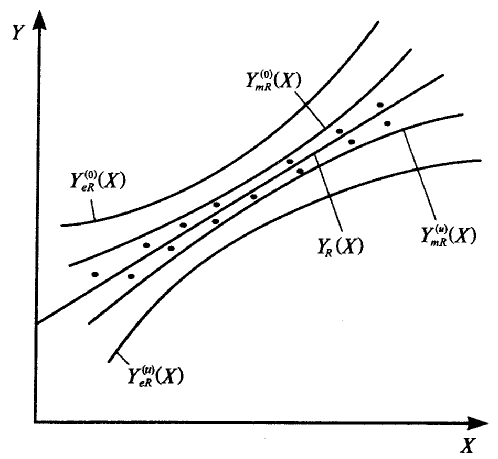Рис.2 – Линейная регрессионная однофакторная модель и ее доверительные интервалы

Дисперсия характеризует точность аппроксимации зависимости прямой линией и определяется по формуле:

(15)

Число степеней свободы этой дисперсии определяется по формуле:

(16)

Расчетное значение F_R сравнивают с табличным значением критерия ФишераF_T, которое определяют по приложению Г при доверительной вероятности р_D = 0,95 и числе степеней свободы дисперсии и . Если F_R < F_T, то гипотеза об адекватности линейного уравнения опытным данным не отвергается. Расчет суммы в формуле (15) сведен в табл. 5.

Таблица 5

u
1 2 3 4 5	2 4 6 8 10	8 16 24 32 40	14 22 30 38 46	14,32 21,72 30,00 37,84 46,32	0,32 -0,28 0,00 -0,16 0,32	0,1024 0,0784 0,0000 0,0256 0,1024
∑	30	-	-	150,20	-	0,3088

---

Используя данные этой таблицы, находим



Подставляя найденные значения дисперсий в формулу (14), получаем

.

Так как <1, то определяем обратное значение отношения дисперсий



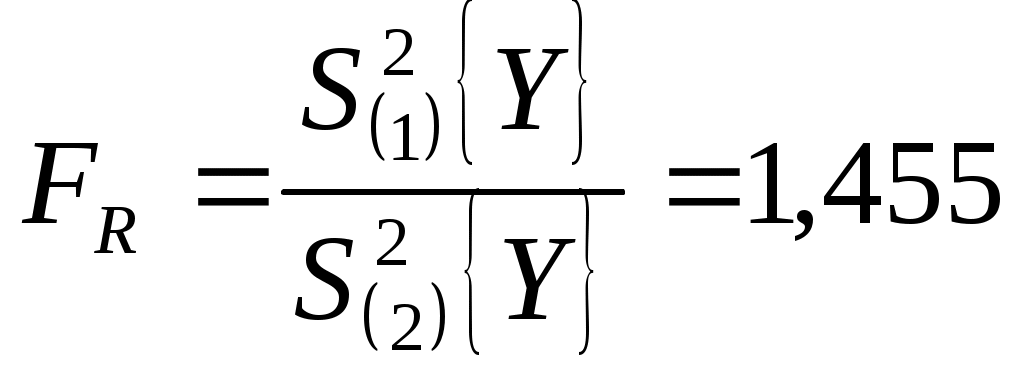
и сравнивая его с табличным значением, которое равно , делаем вывод, что гипотеза об адекватности линейной модели не отвергается.
Восьмая операция – определение значимости коэффициентов регрессии и их доверительных интервалов. Для оценки значимости коэффициентов регрессии используется критерий Стьюдента, расчетное значение которого определяют по формуле:

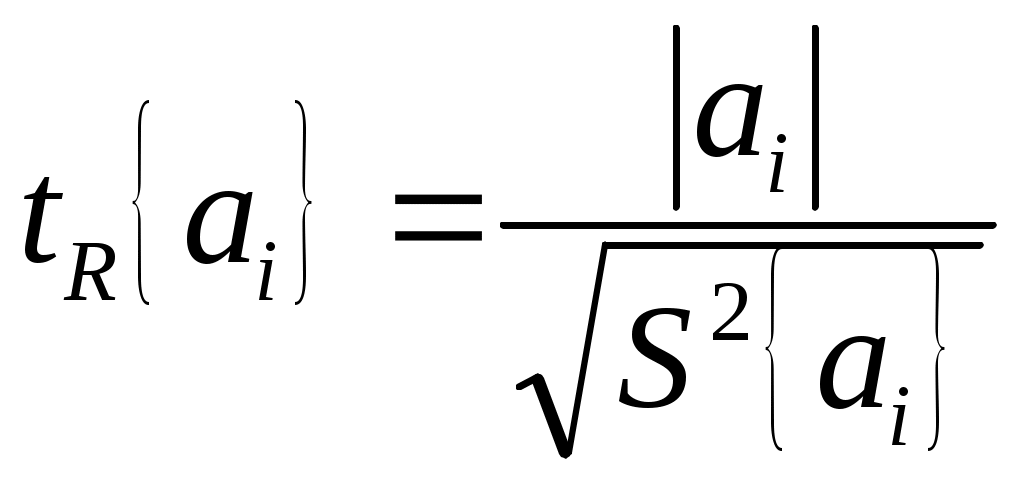(17)

где – дисперсия коэффициента регрессии а_i.

Для определения дисперсий коэффициентов регрессии а₀ и а₁ в уравнении (8) используют формулы:

(18)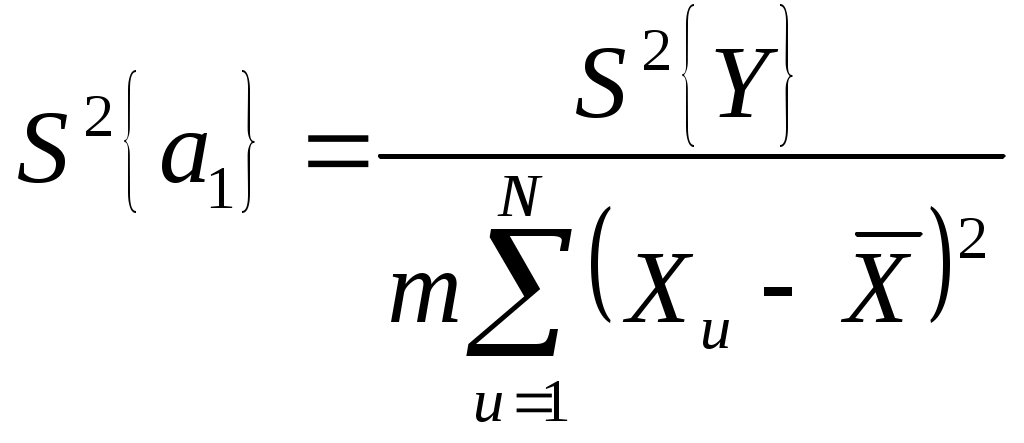

(19)

B формулы (18) и (19) входит диспепсия S²{Y}, которая является сводной оценкой дисперсии случайной величины выходного параметра при условии линейной связи (8). Эта дисперсия определяется по формуле:

(20)

Число степеней свободы этой дисперсии

(21)

---

Подставив в формулу (20) ранее определенные значения и найдем сводную дисперсию случайной величины:



По формулам (18) и (19) определяем дисперсии коэффициентов регрессии:



По приложению В находим табличное значение критерия Стьюдента при условии, что доверительная вероятность и число степеней свободы, определяемое по формуле (21). . Следовательно, . Так как и , полученные коэффициенты значимы и следовательно связь между Y и X значима.

Доверительные абсолютные ошибки коэффициентов регрессии вычисляем по формуле:

(22)

В рассматриваемом примере эти ошибки равны:



Доверительные интервалы для истинных значений коэффициентов регрессии в линейном уравнении (8) определяются неравенством:

(23)

Для рассматриваемого примера доверительные интервалы коэффициентов регрессии при р_D = 0,95 следующие:


Девятая операция — определение доверительных интервалов средних значений выходного параметра при фиксированном значении фактора. Чтобы определить степень отклонения расчетных значений выходного параметра

---

от истинного его значения при каждом уровне фактора определяем доверительные ошибки расчетного значения выходного параметра и доверительные интервалы среднего значения выходного параметра.

Доверительные ошибки расчетных значений выходного параметра для каждого уровня фактора рассчитываем по формуле:

(24)

где – среднеквадратическое отклонение расчетного значения выходного параметра для каждого значения , определяемое по формуле:

(25)

В рассматриваемом примере

Расчеты значений S_m{Y_Ru} для каждого уровня фактора сведены в табл. 6.

Таблица 6

u
1 2 3 4 5	2 4 6 8 10	16 4 0 4 16	861,4·10-4 430,6·10-4 287,2·10-4 430,6·10-4 861,4·10-4	29,34·10-2 20,75·10-2 16,94·10-2 20,75·10-2 29,34·10-2	0,61 0,43 0,35 0,43 0,61	14 22 30 38 46	13,69 21,57 29,65 37,57 45,39	14,61 22,43 30,35 38,43 46,61

---

Смотрите также файлы

• Понятие государства. Основные и неосновные признаки государства.docx

• Сценарий Мы прощаемся с начальной школой.docx

• Учебнометодическое пособие по выполнению лабораторных работ санктпетербург 2023 удк 621. 39(09)(076) ббк 32. 81я73 к 63.docx

• По дисциплине Линейные системы автоматического регулирования комплексного тестирования в магистратуру.docx

• Но очень важная миссия быть классным руководителем. Одни учителя считают эту работу дополнительной нагрузкой к своей преподавательской деятельности, другие называют её самой главной.docx