Подставляя табличное значение критерия Стьюдента в формулу (24), получаем:



В табл. 6 приведены полученные значения , и для каждого уровня фактора. Зная ошибки расчетной величины, можно найти доверительные интервалы для истинных средних значений выходного параметра, используют следующее неравенство:

(26)

На основе приведенных в табл. 6 значений границ доверительного интервала строим графики (см. рис. 2) функции и . Графики этих двух функций образуют своеобразный «коридор». Любое сечение его прямой, параллельной вертикальной оси, соответствует доверительному интервалу, в котором с заданной вероятностью будет находиться истинное среднее значение выходного параметра . Легко заметить, что в этот «коридор» попадают средние экспериментальные значения . Однако некоторые индивидуальные экспериментальные значения выходного параметра в него не попадают, так как интервалы построены для средних значений.
Десятая операция — определение доверительных интервалов для индивидуальных значений выходного параметра при каждом уровне фактора.

Границы доверительного интервала для индивидуальных значений выходного параметра при каждом уровне фактора Х_u определяются по формулам:

где	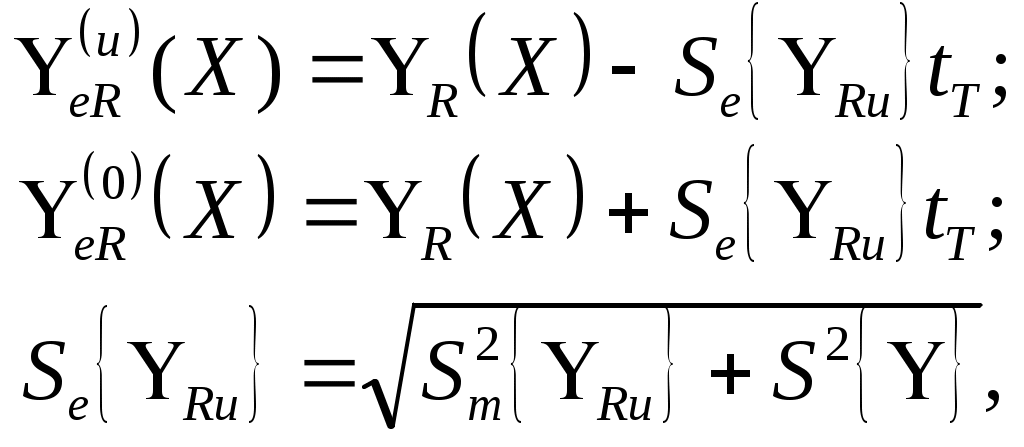(27)
	(28)
	(29)

---

Используя значения из табл. 6 и ранее определенные по уравнению (20) значения и t_T = 2,07, все расчеты верхней границы и нижней границы искомой зоны по формулам (27) и (28) сводим в табл. 7.

Таблица 7

u
1 2 3 4 5	2 4 6 8 10	861,4·10-4 430,6·10-4 287,2·10-4 430,6·10-4 861,4·10-4	8041,4·10-4 7610,6·10-4 7467,2·10-4 7610,6·10-4 8041,4·10-4	0,897 0,872 0,864 0,872 0,897	14 22 30 38 46	1,86 1,81 1,79 1,81 1,86	12,14 20,19 28,21 36,19 44,14	15,86 23,81 31,79 39,81 47,86

Используя данные табл. 7, строим графики функций и (см. рис. 2), которые являются доверительными границами зоны индивидуальных значений выходного параметра. Вероятность попадания точек, соответствующих

---

индивидуальным значениям выходного параметра, равна 0,95, т. е. из ста измерений выходного параметра при любом уровне варьирования фактора 95 измерений попадают в эту зону и только пять не попадают.

Рассматривая индивидуальные значения (см. табл. 3) и границы зоны для каждого , (табл. 7), замечаем, что все индивидуальные измерения попали в доверительную зону, т.е. располагаются между и .

На этом заканчивается статистическая обработка данных рассматриваемого однофакторного эксперимента.

Таким образом, полученная математическая модель, удовлетворяющая условиям адекватности и воспроизодимости процесса и включающая в себя все значимые коэффициенты регрессии имеет окончательный вид: Y_R = 6 + 4X.

12 Общие выводы по работе:

1) Проведённый анализ работ, посвящённых исследованию технологического процесса перематывания основной пряжи, показал, что данная работа имеет научную новизну актуальность и практическую значимость.

2) Проведённые экспериментальные исследования зависимости разрывной нагрузки пряжи перематываемой на мотальной машине М-150-2 от величины массы шайб в натяжном приборе позволили сделать вывод о том, что эта зависимость носит линейный характер.

3) Анализ полученного уравнения и построенного графика (рис. 2), позволяет сделать вывод о том, что с увеличением массы грузовых шайб в натяжном приборе мотальной машины М-150-2 разрывная нагрузка пряжи увеличивается.

---

Список рекомендуемой литературы

1. 
   Хлопкоткачество: Справочник / Букаев П.Т., Оников Э.А. и др. – М.: Легпромбытиздат, 1987. – 576 с.
   
2. 
   Севостьянов А.Г. Методы и средства исследования механико-технологических процессов текстильной промышленности/ Учебное пособие. – М.: МГТУ им. А.Н.Косыгина, 2007. – 648 с.
   
3. 
   Николаев С.Д., Мартынова А.А., Юхин С.С., Власова Н.А. Методы и средства исследования технологических процессов в ткачестве, М.: 2003. – 336 с.
   
4. 
   Назарова М.В., Фефелова Т.Л. Методы и средства исследования технологических процессов ткацкого производства: Учеб пособие/ ВолгГТУ, Волгоград, 2006. – 135 с.
   
5. 
   Гордеев В.А. , Волков П.В. Ткачество - М.: Легкая индустрия, 1970 . – 582 с.
   
6. 
   Назарова М.В., Романов В.Ю. Теория процессов подготовки нитей к ткачеству: учебное пособие/Волгоград, 2004 – 108 с.
   

ПРИЛОЖЕНИЕ А
Таблица критических значений V_Т критерия

исключения резко выделяющихся данных выборки

Число повторности опытов m	Доверительная вероятность PD
	0,99	0,95	0,90
3	1,414	1,412	1,406
4	1,723	1,689	1,645
5	1,955	1,869	1,791
6	2,130	1,996	1,894
7	2,265	2,093	1,974
8	2,374	2,172	2,041
9	2,464	2,237	2,097
10	2,540	2,294	2,146
11	2,606	2,343	2,190
12	2,663	2,387	2,229
13	2,714	2,426	2,264
14	2,759	2,461	2,297
15	2,800	2,493	2,326
16	2,837	2,523	2,354
17	2,871	2,551	2,380
18	2,903	2,577	2,404
19	2,932	2,600	2,426
20	2,959	2,623	2,447
21	2,984	2,644	2,467
22	3,008	2,664	2,486
23	3,030	2,683	2,504
24	3,051	2,701	2,502
25	3,071	2,717	2,537

---

ПРИЛОЖЕНИЕ Б

Табличные значения критерия Кочрена G_T [Р_D=0,95; f = m – 1, N]

N	f
	Доверительная вероятность PD = 0,95
	1	2	3	4	5	6	7	8	9	10	16	36	144	
2	0,9985	0,9750	0,9392	0,9057	0,8772	0,8534	0,8332	0,8159	0,8010	0,7880	0,7341	0,6602	0,5813	0,5000
3	0,9669	0,8709	0,7977	0,7457	0,7071	0,6771	0,6530	0,6333	0,6167	0,6025	0,5466	0,4748	0,4031	0,3333
4	0,9065	0,7679	0,6841	0,6287	0,5859	0,5598	0,5365	0,5175	0,5017	0,4884	0,4366	0,3720	0,3093	0,2500
5	0,8412	0,6838	0,5981	0,5441	0,5065	0,4783	0,4564	0,4387	0,4241	0,4118	0,3645	0,3066	0,2513	0,2000
6	0,7808	0,6161	0,5321	0,4803	0,4447	0,4184	0,3980	0,3817	0,3682	0,3568	0,3135	0,2612	0,2119	0,1667
7	0,7271	0,5612	0,4800	0,4307	0,3974	0,3726	0,3535	0,3384	0,3259	0,3154	0,2756	0,2278	0,1833	0,1429
8	0,6798	0,5157	0,4377	0,3910	0,3595	0,3362	0,3185	0,3043	0,2926	0,2829	0,2462	0,2022	0,1616	0,1250
9	0,6385	0,4775	0,4027	0,3584	0,3286	0,3067	0,2901	0,2768	0,2659	0,2568	0,2226	0,1820	0,1446	0,1111
10	0,6020	0,4450	0,3733	0,3311	0,3029	0,2823	0,2666	0,2541	0,2439	0,2353	0,2032	0,1655	0,1308	0,1000
12	0,5410	0,3924	0,3264	0,2880	0,2624	0,2439	0,2299	0,2187	0,2098	0,2020	0,1737	0,1403	0,1100	0,0833
15	0,4709	0,3346	0,2758	0,2419	0,2195	0,2034	0,1911	0,1815	0,1736	0,1671	0,1429	0,1144	0,0889	0,0667
20	0,3894	0,2705	0,2205	0,1921	0,1735	0,1602	0,1501	0,1422	0,1357	0,1303	0,1108	0,0879	0,0675	0,0500
24	0,3434	0,2354	0,1907	0,1656	0,1493	0,1374	0,1286	0,1216	0,1160	0,1113	0,0094	0,0743	0,0567	0,0417
30	0,2929	0,1980	0,1593	0,1377	0,1237	0,1137	0,1061	0,1002	0,0958	0,0921	0,0771	0,0604	0,0457	0,0333
40	0,2370	0,1576	0,1259	0,1032	0,0968	0,0887	0,0827	0,0780	0,0745	0,0713	0,0595	0,0462	0,0347	0,0250
60	0,1737	0,1131	0,0895	0,0765	0,0682	0,0623	0,0583	0,0552	0,0520	0,0497	0,0411	0,0316	0,0234	0,0167
120	0,0998	0,0632	0,0495	0,0419	0,0371	0,0337	0,0312	0,0292	0,0279	0,0266	0,0218	0,0165	0,0120	0,0083
	0	0	0	0	0	0	0	0	0	0	0	0	0	0

1   2   3   4   5   6   7   8   9   10   11

---

Смотрите также файлы

• Понятие государства. Основные и неосновные признаки государства.docx

• Сценарий Мы прощаемся с начальной школой.docx

• Учебнометодическое пособие по выполнению лабораторных работ санктпетербург 2023 удк 621. 39(09)(076) ббк 32. 81я73 к 63.docx

• По дисциплине Линейные системы автоматического регулирования комплексного тестирования в магистратуру.docx

• Но очень важная миссия быть классным руководителем. Одни учителя считают эту работу дополнительной нагрузкой к своей преподавательской деятельности, другие называют её самой главной.docx