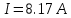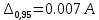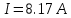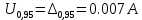Файл: Анализ неопределённости (погрешности) измерений в иис.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 96
Скачиваний: 7
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования и науки Российской Федерации
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «Тюменский индустриальный университет»
Институт геологии и нефтегазодобычи
Кафедра кибернетических систем
ЛАБОРАТОРНАЯ РАБОТА
по дисциплине
«Измерительные информационные системы»
На тему: «Анализ неопределённости (погрешности) измерений в ИИС»
Выполнил: ст.гр. АТПб(до)з-20-2
Надточий Н.И.
Проверил: ст.преподаватель каф. КС
Лапик Н.В.
Тюмень
ТИУ
2022
Цель работы: Основной целью работы является освоение процедуры вычисления неопределенности и приобретение навыков его применения на практике; изучение принципов совместного использования понятий «погрешность измерения» и «неопределенность измерения.
Исходные данные для расчета: Вариант №6
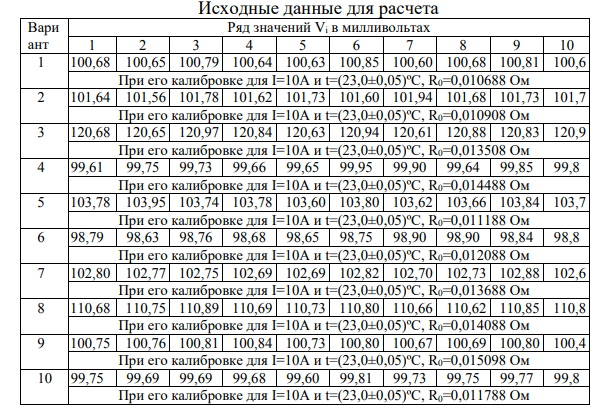
Вариант №6
| Ряд значений Vi в милливольтах: | |||||||||
| 98.79 | 98.63 | 98.76 | 98.68 | 98.65 | 98.75 | 98.90 | 98.90 | 98.84 | 98.8 |
| При его калибровке для I=10A и t=(23,0±0,05)ºС, R0=0,012088 Ом | |||||||||
1) Нахождение результата измерения:
Уравнение измерений:
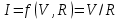,где I - сила тока, V- напряжение, R – сопротивление шунта.
На основе полученных значений вычисляют среднее напряжение по формуле:
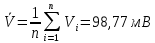
Результат измерения силы тока получают по формулам таблицы 1:
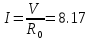A2) Анализ источников погрешности результатов измерений.
2.1) СКО
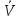, характеризующее случайную составляющую погрешности при измерениях напряжения, вычисляют по формуле:
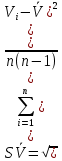мВ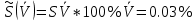
-
данная характеристика приведена в относительном виде.
2.2) Границы не исключенной систематической погрешности вольтметра определены при его калибровке в виде следующего выражения (в выражениях для границ погрешности при разных значениях отклонений от нуля будем опускать ±).
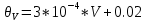
Тогда при
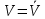получают:
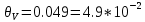мВ,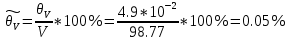
2.3) Границы не исключенной систематической погрешности значения сопротивления шунта, определенные при его калибровке, равны:
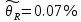
Тогда при ???? = ????0 получают:
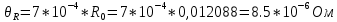
2.4) Границы не исключенной систематической составляющей погрешности значения шунта, обусловленной погрешностью измерений температуры, находят по формуле, определяющей зависимость сопротивления от температуры:
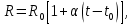
где ????0- значение сопротивления при ???? = ????0 (????0 = 23,00°C);
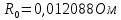
????- температурный коэффициент (???? = 6*10-6 К-1).
В случае, когда границы погрешности измерения температуры равны Δt, границы соответствующей составляющей погрешности значения сопротивления равны:
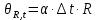
Таким образом, при Δt=0,05°C получаем:
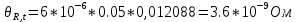
В дальнейшем эту составляющую (ввиду ее малости по сравнению с другими составляющими) можно не учитывать.
3) Вычисления характеристик погрешности результата измерений.
3.1) Делается предположение о равномерном законе распределения не исключенных систематических составляющих погрешности результата измерений внутри границ ???????? и ????????. Тогда СКО суммарной не исключенной систематической составляющей погрешности результата измерений силы тока определяется по формуле:
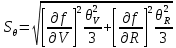
где
,
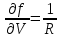
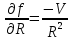- коэффициенты влияния. Таким образом получают: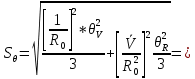
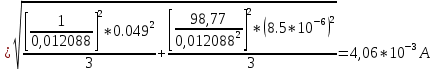
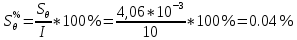
3.2) Доверительные границы суммарной не исключенной систематической составляющей погрешности результата измерений силы тока при доверительной вероятности р=0,95 оценивают по формуле:
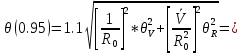
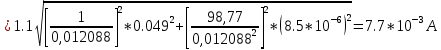
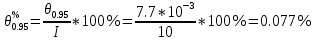
3.3) СКО суммарной погрешности результата измерений силы тока вычисляют по формуле:
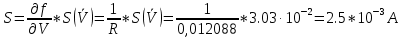
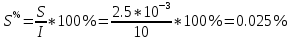
3.4) СКО суммарной погрешности результата измерений силы тока вычисляют по формуле:
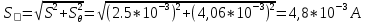
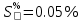
3.5) Доверительные границы погрешности результата измерений силы тока при р=0,95 и числе эффективных степеней свободы ????эфф = ???? − 1 вычисляют по формуле:
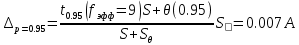
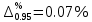
4) Вычисление неопределенностей измерений.
4.1) По типу А вычисляют стандартную неопределенность, обусловленную источниками неопределенности, имеющим случайный характер.
а) Стандартную неопределённость напряжения, обусловленную источниками неопределённости, имеющими случайный характер, определяют по формуле:
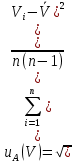мВ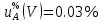
б) Стандартную неопределённость силы тока, обусловленную источниками неопределённости, имеющими случайный характер, определяют по формуле:
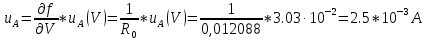
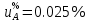
4.2) По типу В вычисляют стандартные неопределенности, обусловленные источниками неопределенности, имеющими систематический характер. Закон распределения величин внутри границ считают равномерным.
а) Границы систематического смещения при измерениях напряжения, определенные при калибровке вольтметра, равны (3 ∙ 10−4 ∙
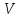+ 0.02)мВ . Тогда соответствующую стандартную неопределённость вычисляют по формуле: 
,
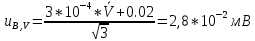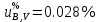
б) Границы, внутри которых лежит значение сопротивления шунта, определены при калибровке шунта и равны 7 ∙ 10−4 ∙ ????. Тогда при ???? = ????0 соответствующую стандартную неопределённость вычисляют по формуле:
,
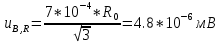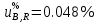
в) Границы изменения сопротивления шунта, обусловленного изменением температуры, равны ???? ∙ ???????? ∙ ????. Тогда при ???? = ????0 соответствующую стандартную неопределённость вычисляют по формуле:
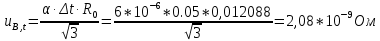
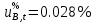
В дальнейшем эту составляющую (ввиду ее малости по сравнению с другими составляющими) можно не учитывать.
г) Суммарную стандартную неопределенность, вычисленную по типу В, определяют по формуле:
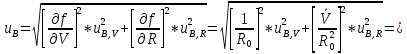
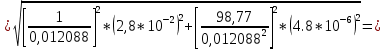
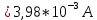
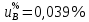
4.3) Суммарную стандартную неопределенность вычисляют по формуле:
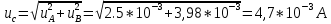
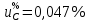
4.4) Эффективное число степеней свободы:
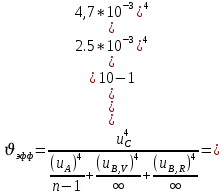
4.5) Коэффициент охвата получают по формуле:
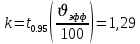
4.6) Расширенную неопределенность определяют следующим образом:
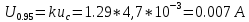
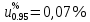
Переход от характеристик погрешности к неопределенности измерений.
Используя оценки характеристик погрешности, полученные в п.п.3 и 4 данной работы, можно продемонстрировать получение оценок неопределенности.
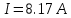
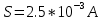
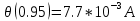
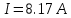
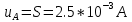
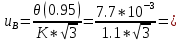
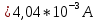
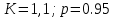
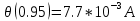
Разность неопределенностей измерений в соответствии с Руководством, и их оценок, меньше погрешности округления при вычислениях
