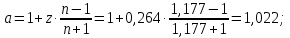ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 365
Скачиваний: 11
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2. Определение диапазонов варьирования входных проектных параметров
3. Обоснование проектных параметров РДТТ
3.1. Определение номинального давления в камере сгорания
3.2. Выбор формы топливного заряда и определение его геометрических характеристик
3.3. Определение массовых и габаритных характеристик РДТТ
2. Определение диапазонов варьирования входных проектных параметров
В качестве входных проектных параметров рассматриваются относительная площадь выходного сечения сопла
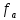 и степень расширения
и степень расширения 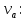
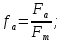
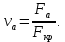
Для определения рациональных диапазонов варьирования данных параметров построим границы области допустимых решений. Рассмотрим следующие основные ограничения:
-
по уровню номинального давления в КС: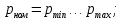
-
по отсутствию перерасширения сопла: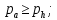
-
по удельному импульсу двигателя: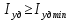 ;
; -
по поперечным габаритам сопла: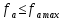 .
.
Принимаем:
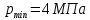 ;
; 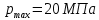 ;
; 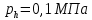 ;
; 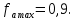
Построение границ области допустимых баллистических решений начнем с определения точек пересечения границ
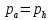 с границами
с границами 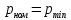 (точка 1) и
(точка 1) и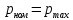 (точка 2). При заданном перепаде давлений приведенная скорость потока в выходном сечении сопла определяется из газодинамической функции:
(точка 2). При заданном перепаде давлений приведенная скорость потока в выходном сечении сопла определяется из газодинамической функции: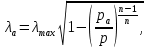
где:
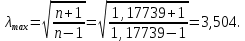
Относительная площадь выходного сечения сопла, необходимая для обеспечения заданного уровня тяги, определяется по формуле:
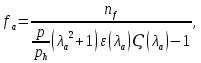
где
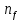 – приведенная тяга:
– приведенная тяга: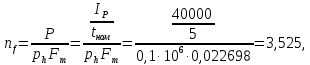
где площадь миделя ЛА:
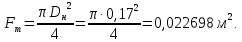
Вместо показателя адиабаты
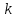 в формулах для
в формулах для 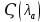 и
и 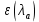 и далее используем показатель политропы
и далее используем показатель политропы 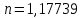 , соответствующий выходному сечению сопла и «замороженному» расширению, если не указано иное.
, соответствующий выходному сечению сопла и «замороженному» расширению, если не указано иное.Поправочный коэффициент
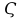 , учитывающий потери тяги и удельного импульса, обусловленные наличием конденсированной фазы в продуктах сгорания, определяются следующим образом:
, учитывающий потери тяги и удельного импульса, обусловленные наличием конденсированной фазы в продуктах сгорания, определяются следующим образом: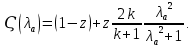
Газодинамическая функция
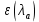 вычисляется по формуле:
вычисляется по формуле: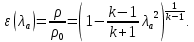
Таким образом, из условий
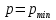 и
и  могут быть определены параметры
могут быть определены параметры 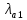 и
и 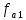 :
: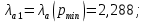
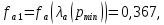
и из условий
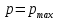 и
и  могут быть определены параметры
могут быть определены параметры 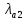 и
и 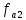 :
: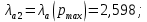
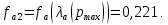
Удельный импульс двигателя, реализуемый в точках 1 и 2, определяется по формуле:
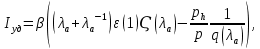
где газодинамическая функция
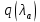 :
: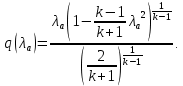
Расходный комплекс
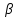 определяется с учетом тепловых потерь в камере (соответствующий поправочный коэффициент при выполнении домашнего задания принимаем равным χ = 0,98) следующим образом:
определяется с учетом тепловых потерь в камере (соответствующий поправочный коэффициент при выполнении домашнего задания принимаем равным χ = 0,98) следующим образом: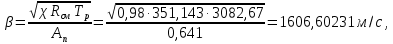
где:
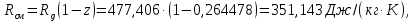
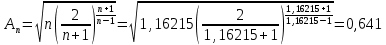
Постоянная расхода
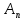 рассчитывается с использованием показателя политропы
рассчитывается с использованием показателя политропы 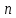 , соответствующего критическому сечению сопла. Тогда:
, соответствующего критическому сечению сопла. Тогда: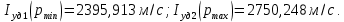
Полученное значение
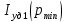 является минимальным на линии 1-2 и в рамках домашнего задания выступает в качестве соответствующего ограничения. Приведенная скорость потока, соответствующая точке пересечения линий
является минимальным на линии 1-2 и в рамках домашнего задания выступает в качестве соответствующего ограничения. Приведенная скорость потока, соответствующая точке пересечения линий  и
и 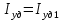 (точка 3) найдем с помощью математического пакета MathCad, а именно с помощью встроенных функций Given и Find, тогда:
(точка 3) найдем с помощью математического пакета MathCad, а именно с помощью встроенных функций Given и Find, тогда: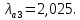
При
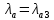 и
и  найдем
найдем 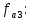
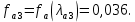
Также для рассматриваемых точек из соответствующих газодинамических функций определяются значения
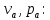
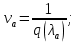
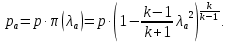
Результаты вычислений представлены в табл. 2.
Таблица 2. Результаты вычислений
| Точка | 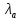 |  |  | 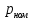 , МПа , МПа | 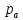 / /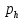 | 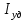 , м/с , м/с |
| 1 | 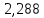 | 6,212 | 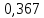 | 4 | 1 | 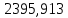 |
| 2 | 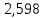 | 21,461 | 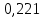 | 20 | 1 | 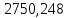 |
| 3 | 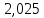 | 3,029 | 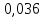 | 20 | 13,441 | 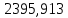 |
Построение границ области допустимых баллистических решений в координатах
(
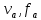 ) удобно осуществлять параметрическим способом. Для этого с некоторым шагом задаются диапазоны значений
) удобно осуществлять параметрическим способом. Для этого с некоторым шагом задаются диапазоны значений  , соответствующие линиям 1-2, 3-2, 3-1. Для данных диапазонов определяются значения
, соответствующие линиям 1-2, 3-2, 3-1. Для данных диапазонов определяются значения  по формуле, представленной выше. Значения
по формуле, представленной выше. Значения  определяются различными способами в зависимости от типа ограничения. Для линии 3-2
определяются различными способами в зависимости от типа ограничения. Для линии 3-2(условие
 ) используется выражение, приведённое выше в настоящей работе; для линий 1-2 (
) используется выражение, приведённое выше в настоящей работе; для линий 1-2 ( ) и 3-1 используются следующие выражения:
) и 3-1 используются следующие выражения: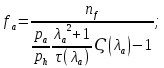
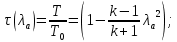
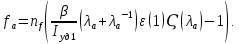
Полученные значения
 используются для графического построения границ области допустимых баллистических решений (рис. 1).
используются для графического построения границ области допустимых баллистических решений (рис. 1).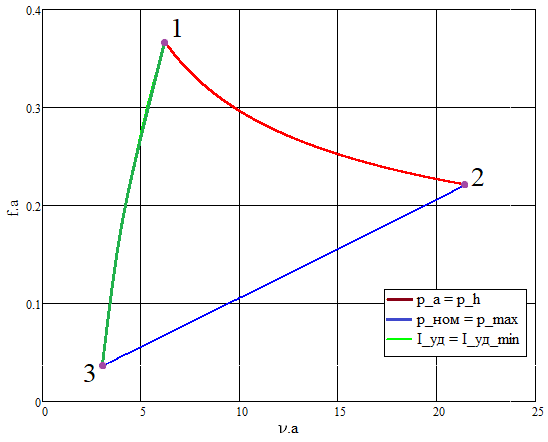
Рис. 1. Область допустимых баллистических решений
В рамках домашнего задания для последующих расчетов выбирается одно значение
 и соответствующий ему диапазон
и соответствующий ему диапазон  или
или  из области допустимых баллистических решений. В качестве опорного решения рассмотрим:
из области допустимых баллистических решений. В качестве опорного решения рассмотрим: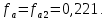
Минимальное значение
 , соответствующее выбранному
, соответствующее выбранному  , определяется как больший из корней квадратного уравнения
, определяется как больший из корней квадратного уравнения 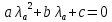 с коэффициентами:
с коэффициентами: