Добавлен: 05.12.2023
Просмотров: 318
Скачиваний: 10
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Волны на поверхности
Волны на поверхности воды
Если сместить участок поверхности жидкости от положения равновесия, то под действием возвращающих сил поверхность начинает двигаться обратно к равновесному положению. Это движение, однако, не останавливается, а превращается в колебательное движение около равновесного положения и распространяется на другие участки. Так возникают волны на поверхности жидкости.
Если возвращающая сила — это преимущественно силы тяжести, то такие волны называются гравитационными волнами (не путать с волнами гравитации). Гравитационные волны на воде можно видеть повсеместно.
Если возвращающая сила — это преимущественно сила поверхностного натяжения, то такие волны называются капиллярными.
Если эти силы сопоставимы, такие волны называются капиллярно-гравитационными.
Волны на поверхности жидкости затухают под действием вязкости и других факторов.
Сосуществование с другими фазами
Формально говоря, для равновесного сосуществования жидкой фазы с другими фазами того же вещества — газообразной или кристаллической — нужны строго определённые условия. Так, при данном давлении нужна строго определённая температура. Тем не менее, в природе и в технике повсеместно жидкость сосуществует с паром, или также и с твёрдым агрегатным состоянием — например, вода с водяным паром и часто со льдом (если считать пар отдельной фазой, присутствующей наряду с воздухом). Это объясняется следующими причинами:
-
Неравновесное состояние. Для испарения жидкости нужно время, пока жидкость не испарилась полностью, она сосуществует с паром. В природе постоянно происходит испарение воды, также как и обратный процесс — конденсация. -
Замкнутый объём. Жидкость в закрытом сосуде начинает испаряться, но поскольку объём ограничен, давление пара повышается, он становится насыщенным ещё до полного испарения жидкости, если её количество было достаточно велико. При достижении состояния насыщения количество испаряемой жидкости равно количеству конденсируемой жидкости, система приходит в равновесие. Таким образом, в ограниченном объёме могут установиться условия, необходимые для равновесного сосуществования жидкости и пара. -
Присутствие атмосферы в условиях земной гравитации. На жидкость действует атмосферное давление (воздух и пар), тогда как для пара должно учитываться практически только его парциальное давление. Поэтому жидкости и пару над её поверхностью соответствуют разные точки на фазовой диаграмме, в области существования жидкой фазы и в области существования газообразной соответственно. Это не отменяет испарения, но на испарение нужно время, в течение которого обе фазы сосуществуют. Без этого условия жидкости вскипали бы и испарялись очень быстро.
Силы, действующие в жидкости
Жидкости делятся на покоящиеся и движущиеся.
Здесь же рассмотрим силы, которые действуют на жидкость и вне ее в общем случае.
Сами эти силы можно разделить на две группы.
1. Силы массовые. По-другому эти силы называют силами, распределенными по массе: на каждую частицу с массой M = W действует сила F, в зависимости от ее массы.
Пусть объем W содержит в себе точку А. Тогда в точке А:
где FА – плотность силы в элементарном объеме.
Плотность массовой силы – векторная величина, отнесена к единичному объему W; ее можно проецировать по осям координат и получить: Fx, Fy, Fz. То есть плотность массовой силы ведет себя, как массовая сила.
Примерами этих сил можно назвать силы тяжести, инерции (кориолисова и переносная силы инерции), электромагнитные силы.
Однако в гидравлике, кроме особых случаев, электромагнитные силы не рассматривают.
2. Поверхностные силы. Таковыми называют силы, которые действуют на элементарную поверхность w, которая может находиться как на поверхности, так и внутри жидкости; на поверхности, произвольно проведенной внутри жидкости.
Таковыми считают силы: силы давления которые составляют нормаль к поверхности; силы трения которые являются касательными к поверхности.
Если по аналогии (1) определить плотность этих сил, то:
нормальное напряжение в точке А:
касательное напряжение в точке А:
И массовые, и поверхностные силы могут быть внешними, которые действуют извне и приложены к какой-то частице или каждому элементу жидкости; внутренними, которые являются парными и их сумма равна нулю.
Давление
Давление — величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности
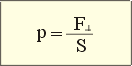
где
p – давление, Па
F – приложенная сила давления, Н
S – площадь поверхности / иначе площадь опоры тела /, м2
Давление — величина скалярная.
Единица СИ давления:

Единица, не входящая в СИ: бар = 10 5 Па.
Единицы допускавшиеся к применению до 1980 г.:
-
миллиметр ртутного столба (мм рт. ст.) -
физическая атмосфера (атм) = 760 мм рт. ст. -
техническая атмосфера (ат) = 1 кгс/(см2)
Приборы для измерения давления. Для измерения давления используют жидкостные (барометр, пьезометр, вакуумметр, дифманометр), механический манометр.
Для измерения давления используют жидкостные (барометр, пьезометр, вакуумметр, дифманометр), механические (манометр, вакуумметр) и электрические приборы. Рассмотрим принцип действия основных из них.
Барометр состоит из открытой чашки, заполненной ртутью, и стеклянной трубки, верхний конец которой запаян,
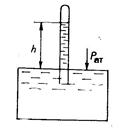 | а нижний опущен в чашку под уровень ртути. В верхней части трубки воздуха нет, поэтому в ней действует давление насыщенных паров ртути |
| Ртутный барометр | |
где
Пьезометр - это прибор для измерения небольших давлений в жидкости при помощи высоты столба этой жидкости.
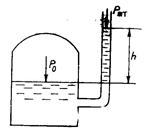 | Он состоит из вертикальной стеклянной трубки, верхний конец которой открыт и сообщается с атмосферой, а нижний присоединен к сосуду, в котором измеряют давление р. |
| Пьезометр | |
По основному уравнению гидростатики
Вакуумметр - это U-образная стеклянная трубка, в колене которой имеется жидкость, тяжелее от той, которая
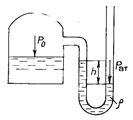 | находится в сосуде. Один конец трубки соединен с сосудом, а второй открыт (рис.2.7). Давление |
| Жидкостной вакууметр | |
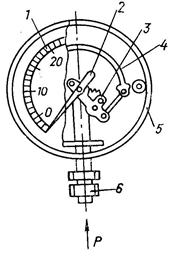
Пружинный манометр состоит из корпуса 5, штуцера 6, манометрической (пружинной) трубки 4, передающего механизма 3, стрелки 2 и шкалы 1. Жидкость под давлением попадает в штуцер, а затем в трубку. Под действием давления трубка разгибается и перемещается ее свободный конец, связанный со стрелкой прибора.
| | |
| | |
2. Гидростатика
Гидростатика – раздел гидравлики, изучающий законы равновесия жидкости и их применение.
Напряжение в жидкости описывается давлением.
Давление (р) – величина, равная отношению модуля силы давления F, действующей перпендикулярно поверхности, к площади этой поверхности.
p=F/S (Н/м2)
При равномерном распределении сил давления, давление на всех участках поверхности одинаково и численно равно силе давления, действующую на поверхность единичной площади.
Рассмотрим наиболее важный для практики частный случай равновесия жидкости, находящейся под действием только сил тяжести.
 Рассмотрим закрытый сосуд, в котором находится жидкость.
Рассмотрим закрытый сосуд, в котором находится жидкость. Обозначим через р0внешнее поверхностное давление, т.е. давление на свободную поверхность жидкости.
Наметим точку А, у которой выделим единицу массы жидкости. К этой единице массы приложена объемная сила – сила тяжести.
Тогда давление в произвольной точке А выразится зависимостью:
р=-ρ gZ+(р0+ρ gZ0) или р=р0+ρ g(Z0-Z)=р0+ρ gh.
Давление р, определяемое по этой формуле, называется абсолютным давлением. рабс=р0+ ρ gh- уравнение и является основным уравнением гидростатики в простейшей гидравлической форме.
Величина ρgh представляет собой ту часть абсолютного давления рабс, которая обусловлена весом самой жидкости. Назовем ее весовым давлением.
рвес=ρ gh.
Основное уравнение гидростатики показывает, что абсолютное давление в точке равно сумме внешнего поверхностного давления р0 и весового давления(ρgh)
Разность между абсолютным гидростатическим давлением и атмосферным называется избыточным или манометрическим давлением (такое давление показывает механический манометр):
ризб=рабс – рат.
Если р0=ратм, то из основного уравнения гидростатики следует, что
рабс=ратм+ρ gh и рабс – ратм=ризб=ρ gh
т.е. избыточное давление равно весовому.
По основному уравнению гидростатики можно определить абсолютное давление в любой точке покоящейся жидкости.
Если взять ряд точек, в которых гидростатическое давление одинаково, и провести через эти точки поверхность, то получим поверхность равного давления.
Закон Паскаля