Добавлен: 05.12.2023
Просмотров: 325
Скачиваний: 10
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
будет отличаться от такового для жидкости, находящейся в покое;
3. удельная потенциальная энергия (т. е. потенциальная энергия единицы веса жидкости) по отношению к некоторой плоскости сравнения для всех точек данного сечения потока жидкости есть величина постоянная.
Понятие жидкости. Реальная и идеальная жидкости
Жидкость – физическое тело, молекулы которого слабо связаны между содой. Поэтому незначительные силы способны легко изменить форму жидкости, которая способна сохранить объем, но не форму.
В гидравлике жидкость рассматривают как непрерывную среду, заполняющую пространство без пустот и промежутков, т.е. отвлекаются от молекулярного строения жидкости и её частицы, даже бесконечно малые, считают состоящими из большого числа молекул.
Реальной жидкостью называют жидкость, обладающую вязкостью (свойство жидкости сопротивляться сдвигу ее слоев).
Идеальная или невязкая жидкость является упрощенной моделью реальной (вязкой) жидкости. По предположению, идеальная жидкость имеет все свойства реальной, кроме вязкости.
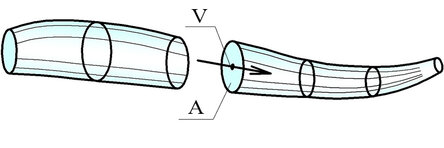
Трубка тока – поверхность, очерченная вдоль небольшого контура внутри которой вдоль линии тока перемещаются частицы жидкости. Стенки трубки тока непроницаемы. Площадь поперечного сечения трубки тока мала, поэтому скорости движения в каждой точке равны (см. рис. 2.34).

Рис. 2.34. Трубка тока
Элементарная струйка – поток жидкости, протекающий в трубке тока Элементарную струйку можно представить также как совокупность линий тока, проходящих через бесконечно малое сечение ds, а разность скоростей соседних линий тока бесконечно мала. Расход элементарной струйки dq = uds. Поток жидкости можно представить как совокупность трубок тока, в которых движутся элементарные струйки.
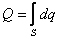 .
.
Средняя скорость потока– скорость, одинаковая в каждой точке потока в данном сечении, соответствует реальному расходу
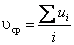 ,
,
где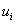 – скорость в точке в данном сечении; i– количество точек.
– скорость в точке в данном сечении; i– количество точек.
Для потока жидкости, состоящего из нескольких трубок тока можно записать
где S – площадь сечения потока жидкости.
Живым или нормальным называют сечение потока перпендикулярное направлению скорости течения (линиям тока).
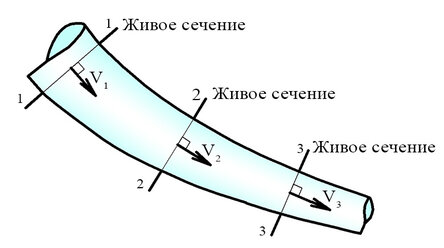
На рисунке изображен поток жидкости, в произвольных точках выбраны перпендикулярные направлениям скоростей живые сечения 1-1, 2-2, 3-3.
Периметр контакта жидкости в данном живом сечении называют смоченным периметром (П, м).
Рассмотрим пример:
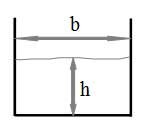
Для представленного сечения смоченный периметр можно определить по формуле:
П=2h+b
Отношение площади живого сечения (А, м2) к смоченному периметру (П, м) называют гидравлическим радиусом.
Rг=А/П, м
Рассмотрим трубу с внутренним диаметром d, полностью заполненную жидкостью.

П=π d
A=π d2/4
Rг=d/4, м
Для заполненной круглой трубы гидравлический диаметр можно определить по формуле:
Dг=4Rг, м
Dг=(4*S)/P
Рассмотрим стационарное течение жидкости на участках с плавной изменяемостью движения.
Расход потока - это количество жидкости, проносимое потоком сквозь живое сечение за единицу времени.
Q=V×A
где Q - объемный расход, А - площадь живого сечения.
Поскольку количество жидкости может измеряться в единицах объема, массы, веса различают:
Формула связи весового, массового и объемного расхода:
G=gm=ρgQ
где ρ - плотность жидкости, g - ускорение свободного падения
При отсутствии притока и оттока жидкости, согласно уравнению неразрывности, расход несжимаемой жидкости остается постоянным.
Доступным и точным методом измерения расхода является объемный способ, в котором фиксируется время наполнения нормированной емкости.
В системе СИ расход измеряют в м3/с, при нормировании характеристик устройств часто используют величину л/мин, для пересчета величин используйте калькулятор единиц измерения расхода, представленный на нашем сайте.
Среднюю скорость можно определить используя зависимость:
V=Q/A
где Q - объемный расход, А - площадь живого сечения.
Если рассматривать поток, как множество элементарных струек, то следует понимать, что скорость движения жидкости в каждом из потоков может отличаться от среднего значения. Средняя скорость - это абстрактное понятие, которое дает возможность рассматривать поток, как единое целое. Такой подход позволяет решить множество инженерных задач при движении жидкости в трубопроводах, каналах и т.д.
Рассчитать скорость при известных значениях расхода и площади можно с помощью калькулятора скорости потока жидкости.
7. Уравнение сплошности или неразрывности (материальный баланс)

Уравнение неразрывности это уравнение материального баланса или иначе закон сохранения массы Если в сплошной среде выделить произвольный объем V , то очевидно Изменение массы во времени Возможно лишь за счет притока жидкости, который равен суммарному массовому расходу жидкости через поверхность s объема V
Рассмотрим установившееся движение потока идеальной несжимаемой жидкости, на которую действует только одна массовая сила - сила тяжести.
Выбреем два живых сечения , 1-1 в начале рассматриваемого участка, 2-2 - в конце.
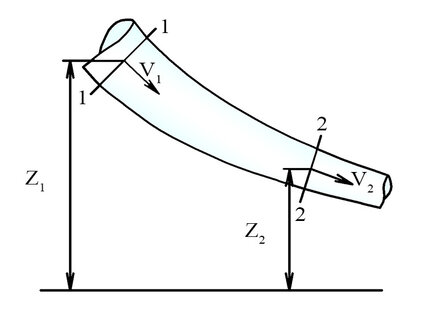
Запишем для этого случая уравнение, связывающее между собой скорость движения жидкости и ее давление в каждом сечении.
z1 + (p1/ρg) + (V12/2g) = z2 + (p2/ρg) + (V22/2g)
Указанное уравнение называют законом или уравнением Бернулли для элементарной струйки идеальной несжимаемой жидкости.
Для каждого рассматриваемого сечения полный напор есть сумма геометрического, пьезометрического и скоростного напора. Для идеальной жидкости (т.е. при отсутствии потерь энергии) полный напор - величина постоянная.
z + p/ρg + V2/2g = Н = const
Уравнение Бернулли можно записать и в другом виде, умножим обе части уравнения на g получим:
gz1 + p1/ρ + V12/2 = gz2 + p2/ρ + V22/2
Составляющие уравнения Бернулли являются различными формами удельной (отнесенной к единице массы) механической энергии жидкости:
3. удельная потенциальная энергия (т. е. потенциальная энергия единицы веса жидкости) по отношению к некоторой плоскости сравнения для всех точек данного сечения потока жидкости есть величина постоянная.
Понятие жидкости. Реальная и идеальная жидкости
Жидкость – физическое тело, молекулы которого слабо связаны между содой. Поэтому незначительные силы способны легко изменить форму жидкости, которая способна сохранить объем, но не форму.
В гидравлике жидкость рассматривают как непрерывную среду, заполняющую пространство без пустот и промежутков, т.е. отвлекаются от молекулярного строения жидкости и её частицы, даже бесконечно малые, считают состоящими из большого числа молекул.
Реальной жидкостью называют жидкость, обладающую вязкостью (свойство жидкости сопротивляться сдвигу ее слоев).
Идеальная или невязкая жидкость является упрощенной моделью реальной (вязкой) жидкости. По предположению, идеальная жидкость имеет все свойства реальной, кроме вязкости.

Элементарная струйка и поток.
Трубка тока – поверхность, очерченная вдоль небольшого контура внутри которой вдоль линии тока перемещаются частицы жидкости. Стенки трубки тока непроницаемы. Площадь поперечного сечения трубки тока мала, поэтому скорости движения в каждой точке равны (см. рис. 2.34).

Рис. 2.34. Трубка тока
Элементарная струйка – поток жидкости, протекающий в трубке тока Элементарную струйку можно представить также как совокупность линий тока, проходящих через бесконечно малое сечение ds, а разность скоростей соседних линий тока бесконечно мала. Расход элементарной струйки dq = uds. Поток жидкости можно представить как совокупность трубок тока, в которых движутся элементарные струйки.
Средняя скорость потока– скорость, одинаковая в каждой точке потока в данном сечении, соответствует реальному расходу
где
Для потока жидкости, состоящего из нескольких трубок тока можно записать
| | 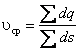 или или | |
где S – площадь сечения потока жидкости.
Живое сечение
Живым или нормальным называют сечение потока перпендикулярное направлению скорости течения (линиям тока).

На рисунке изображен поток жидкости, в произвольных точках выбраны перпендикулярные направлениям скоростей живые сечения 1-1, 2-2, 3-3.
Смоченный периметр
Периметр контакта жидкости в данном живом сечении называют смоченным периметром (П, м).
Рассмотрим пример:

Для представленного сечения смоченный периметр можно определить по формуле:
П=2h+b
Гидравлический радиус
Отношение площади живого сечения (А, м2) к смоченному периметру (П, м) называют гидравлическим радиусом.
Rг=А/П, м
Гидравлический радиус для круглой трубы
Рассмотрим трубу с внутренним диаметром d, полностью заполненную жидкостью.

П=π d
A=π d2/4
Rг=d/4, м
Гидравлический диаметр
Для заполненной круглой трубы гидравлический диаметр можно определить по формуле:
Dг=4Rг, м
Гидравлический диаметр (эквивалентный диаметр) обычно обозначается — dг, dh, Dг. Широко применяется при гидравлических и аэродинамических расчетах различных систем, где формой сечения каналов не является окружность. Гидравлический (эквивалентный) диаметр может служит мерой эффективности системы в пропускании потока жидкости или газа.
Классическая формула гидравлического диаметра (эквивалентного диаметра)
Dг=(4*S)/P
Расход и средняя скорость течения жидкости
Рассмотрим стационарное течение жидкости на участках с плавной изменяемостью движения.

Массовый, объемный и весовой расход
Расход потока - это количество жидкости, проносимое потоком сквозь живое сечение за единицу времени.
Q=V×A
где Q - объемный расход, А - площадь живого сечения.
Поскольку количество жидкости может измеряться в единицах объема, массы, веса различают:
-
массовый расход m, кг/с -
объемный расход Q, л/с, м3/с -
весовой расход G, H/c
Формула связи весового, массового и объемного расхода:
G=gm=ρgQ
где ρ - плотность жидкости, g - ускорение свободного падения
При отсутствии притока и оттока жидкости, согласно уравнению неразрывности, расход несжимаемой жидкости остается постоянным.
Объемный способ измерения расхода
Доступным и точным методом измерения расхода является объемный способ, в котором фиксируется время наполнения нормированной емкости.
В системе СИ расход измеряют в м3/с, при нормировании характеристик устройств часто используют величину л/мин, для пересчета величин используйте калькулятор единиц измерения расхода, представленный на нашем сайте.
Средняя скорость потока
Среднюю скорость можно определить используя зависимость:
V=Q/A
где Q - объемный расход, А - площадь живого сечения.
Если рассматривать поток, как множество элементарных струек, то следует понимать, что скорость движения жидкости в каждом из потоков может отличаться от среднего значения. Средняя скорость - это абстрактное понятие, которое дает возможность рассматривать поток, как единое целое. Такой подход позволяет решить множество инженерных задач при движении жидкости в трубопроводах, каналах и т.д.
Рассчитать скорость при известных значениях расхода и площади можно с помощью калькулятора скорости потока жидкости.
7. Уравнение сплошности или неразрывности (материальный баланс)

Уравнение неразрывности это уравнение материального баланса или иначе закон сохранения массы Если в сплошной среде выделить произвольный объем V , то очевидно Изменение массы во времени Возможно лишь за счет притока жидкости, который равен суммарному массовому расходу жидкости через поверхность s объема V
Уравнение Бернулли для потока идеальной жидкости
Рассмотрим установившееся движение потока идеальной несжимаемой жидкости, на которую действует только одна массовая сила - сила тяжести.
Выбреем два живых сечения , 1-1 в начале рассматриваемого участка, 2-2 - в конце.

Запишем для этого случая уравнение, связывающее между собой скорость движения жидкости и ее давление в каждом сечении.
z1 + (p1/ρg) + (V12/2g) = z2 + (p2/ρg) + (V22/2g)
-
где z - геометрическая высота, -
p - давление в выбранном сечении, -
V - скорость жидкости в выбранном сечении, -
ρ - плотность жидкости, -
g - ускорение свободного падения.
Указанное уравнение называют законом или уравнением Бернулли для элементарной струйки идеальной несжимаемой жидкости.
Для каждого рассматриваемого сечения полный напор есть сумма геометрического, пьезометрического и скоростного напора. Для идеальной жидкости (т.е. при отсутствии потерь энергии) полный напор - величина постоянная.
z + p/ρg + V2/2g = Н = const
-
где z - геометрический напор, -
p/ρg - пьезометрический напор, -
z + p/ρg - статический напор, -
V2/2g - скоростной напор, -
z + p/ρg + V2/2g = Н - полный напор.
Уравнение Бернулли можно записать и в другом виде, умножим обе части уравнения на g получим:
gz1 + p1/ρ + V12/2 = gz2 + p2/ρ + V22/2
Физический смысл уравнения Бернулли
Составляющие уравнения Бернулли являются различными формами удельной (отнесенной к единице массы) механической энергии жидкости:
-
gz - удельная энергия положения, -
p/ρ - удельная энергия давления движущейся жидкости, -
V12/2 - удельная кинетическая энергия жидкости, -
gz + p/ρ + V2/2 = Hg - полная удельная энергия движущейся идеальной жидкости.