Добавлен: 05.12.2023
Просмотров: 317
Скачиваний: 10
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, можно привести и это уравнение к виду:

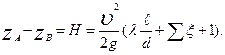
Формулы тождественны между собой, и гидравлические расчеты для обеих схем трубопровода будут одинаковы.
Различие состоит лишь в том, что при истечении под уровень, единица, стоящая в скобках в правой части, представляет собой коэффициент сопротивления «на выход» потока под уровень, в то время как при истечении в атмосферу она учитывает кинетическую энергию, оставшуюся в потоке после выхода из трубопровода, которая может быть так или иначе использована.
Таким образом, напор Н при истечении под уровень равен сумме всех сопротивлений: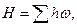 при истечении же в атмосферу он делится на две части: кинетическую энергию, уносимую потоком из трубы, и сумму потерь напора
при истечении же в атмосферу он делится на две части: кинетическую энергию, уносимую потоком из трубы, и сумму потерь напора
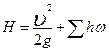 .
.
Гидравлический расчет простого трубопровода сводится к решения трех основных задач (для заданных конфигураций трубопровода, его материала и длины).
Первая задача. Требуется определить напор Н, необходимый для пропуска заданного расхода жидкости Q по заданному трубопроводу диаметром d и длиной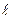 (шероховатость известна). Задача решается путем непосредственного использования формулы с предварительным вычислением средней скорости
(шероховатость известна). Задача решается путем непосредственного использования формулы с предварительным вычислением средней скорости
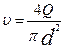 .
.
Тогда искомый напор
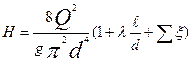
Определение значений коэффициентов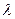 и
и 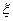 в данной задаче не вызывает затруднений, они находятся на основании известного числа Re (легко находится) и относительной шероховатости трубопровода.
в данной задаче не вызывает затруднений, они находятся на основании известного числа Re (легко находится) и относительной шероховатости трубопровода.
Вторая задача. Требуется определить пропускную способность (расход) трубопровода Q при условии, что известны напор Н, длина трубы
 и ее диаметр d (и шероховатость). Задача решается с помощью формулы, согласно которой
и ее диаметр d (и шероховатость). Задача решается с помощью формулы, согласно которой
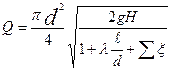
Т.к. коэффициенты и
и  являются функциями числа Re, которое связано с неизвестным и искомым здесь расходом Q, то решение находим методом последовательных приближений, полагая в первом приближении существование квадратичного закона сопротивления, при котором коэффициенты
являются функциями числа Re, которое связано с неизвестным и искомым здесь расходом Q, то решение находим методом последовательных приближений, полагая в первом приближении существование квадратичного закона сопротивления, при котором коэффициенты  и
и  не зависят от числа Re (а определяются только относительной шероховатостью стенок трубопроводов).
не зависят от числа Re (а определяются только относительной шероховатостью стенок трубопроводов).
Третья задача. Требуется определить диаметр трубопровода d при заданных значениях Q, и Н. Здесь также используем формулу, но встречаемся с трудностями в вычислениях вследствие того, что Re неизвестно, неизвестна следовательно и
и Н. Здесь также используем формулу, но встречаемся с трудностями в вычислениях вследствие того, что Re неизвестно, неизвестна следовательно и  . Решение задачи производится также методом последовательных приближений, полагая в первом приближении наличие квадратичного закона сопротивления, при котором коэффициент
. Решение задачи производится также методом последовательных приближений, полагая в первом приближении наличие квадратичного закона сопротивления, при котором коэффициент  является функцией только диаметра (при заданной шероховатости стенок трубы)
является функцией только диаметра (при заданной шероховатости стенок трубы)
Тогда уравнение приводится к виду
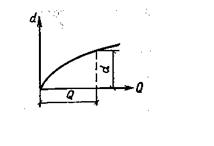
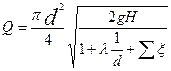 .
.
Задаваясь рядом значений диаметра d1, d2, …,du и вычисляя по последней формуле соответственно Q1, Q2, …, Qu, строим график Q=f(t), из которого определяем диаметр, отвечающий заданному расходу.
11.Основы подземной гидравлики.
Процессы движения жидкостей, газа и воды сквозь пористые породы изучает раздел подземной гидравлики. Расчетные модели базируются на классических положениях гидравлики, однако главной особенностью являются наличие пористой среды, поэтому законы и зависимости имеют отличия. Подземная гидравлика изучает процессы фильтрации. Основной задачей подземной гидравлики является расчет дебитов скважин и их параметров. Структура скважины представлена на рис. 4.1.
Фильтрация - движение жидкостей, газов и их смесей в пористых и трещиноватых средах, в твердых телах, пронизанной системой сообщающихся между собой пор и микротрещин.
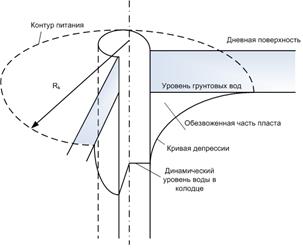
Рис. 4.1. Схема поверхностей фильтрации в пласте с грунтовыми водами
Фильтрация жидкостей и газов по сравнению с движением в трубах и каналах обладает некоторыми особенностями, а именно происходит по чрезвычайно малым в поперечных размерах поровым каналам при очень малых скоростях движения жидкостей. При этом, поскольку площади соприкосновения жидкости с твердыми частицами при движении жидкости в пористой велики, велики и силы трения.
Пористая среда характеризуется коэффициентами пористости и просветности.
Активная пористость (пористость) - безразмерная величина, характеризующая способность пористой среды пропускать жидкость, учитывает только те поры и микротрещины, которые соединены между собой и через которые может фильтроваться жидкость.
Коэффициент пористости m - отношение объема пор (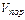 ) ко всему объему пористой среды (
) ко всему объему пористой среды ( 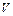 ):
):
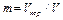 . (4.1)
. (4.1)
Коэффициентом просветности n - отношение площади просветов (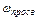 ) в данном сечении пористой среды ко всей площади этого сечения (
) в данном сечении пористой среды ко всей площади этого сечения ( 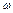 ):
):
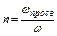
 (4.2)
(4.2)
Среднее по длине пласта значение просветности равно пористости, т.е.
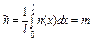 , (4.3)
, (4.3)
Поэтому среднее значение площади просветов
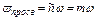
Скоростью фильтрации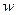 называется отношение объемного расхода жидкости к площади поперечного сечения пласта, нормального к направлению движения жидкости
называется отношение объемного расхода жидкости к площади поперечного сечения пласта, нормального к направлению движения жидкости
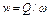 (4.6)
(4.6)
Скорость фильтрации представляет собой фиктивную скорость, с которой двигалась бы жидкость, если бы пористая среда отсутствовала (m=1), поэтому для более корректной характеристики скорости используют понятие средней скорости движения жидкости. Скорость фильтрации и средняя скорость движения связана соотношением:
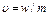 (4.8)
(4.8)
В общем виде средняя скорость движения жидкости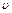 равна отношению объемного расхода к площади просветов
равна отношению объемного расхода к площади просветов 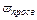 (живому сечению потока):
(живому сечению потока):
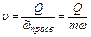 (4.7)
(4.7)
Коэффициент фильтрации с – скорость фильтрации при градиенте давления равном единице, зависит от свойств пористой среды и от свойств фильтрующейся жидкости.
Проницаемость - способность пористой среды пропускать сквозь себя жидкости и газы, характеризуется коэффициентом проницаемости. В отличии от коэффициента фильтрации с коэффициент проницаемости k зависит от свойств пористой среды.
Коэффициент проницаемости и фильтрации связаны соотношением
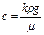 (4.8)
(4.8)
Коэффициент проницаемости имеет размерность площади, а коэффициент фильтрации — размерность скорости.
На практике проницаемость нефтяных и газовых пластов измеряется единицами, называемыми дарси (Д). За единицу проницаемости 1 Д принимают проницаемость такой пористой среды, при фильтрации через образец которой площадью 1 см2, длиной 1 см при перепаде давления в 1 кгс/см2 (98100 Па) расход жидкости вязкостью 1 сП (1 мПа с) составляет 1 см3/с.
с) составляет 1 см3/с.
Для перевода в систему СИ справедливо соотношение:
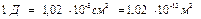 .
.
Проницаемость реальных пластов изменяется от нескольких миллидарси до нескольких дарси.
Формулы тождественны между собой, и гидравлические расчеты для обеих схем трубопровода будут одинаковы.
Различие состоит лишь в том, что при истечении под уровень, единица, стоящая в скобках в правой части, представляет собой коэффициент сопротивления «на выход» потока под уровень, в то время как при истечении в атмосферу она учитывает кинетическую энергию, оставшуюся в потоке после выхода из трубопровода, которая может быть так или иначе использована.
Таким образом, напор Н при истечении под уровень равен сумме всех сопротивлений:
Гидравлический расчет простого трубопровода сводится к решения трех основных задач (для заданных конфигураций трубопровода, его материала и длины).
Первая задача. Требуется определить напор Н, необходимый для пропуска заданного расхода жидкости Q по заданному трубопроводу диаметром d и длиной
Тогда искомый напор
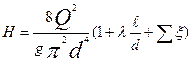
Определение значений коэффициентов
Вторая задача. Требуется определить пропускную способность (расход) трубопровода Q при условии, что известны напор Н, длина трубы
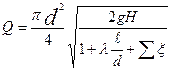
Т.к. коэффициенты
Третья задача. Требуется определить диаметр трубопровода d при заданных значениях Q,
Тогда уравнение приводится к виду

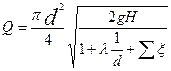 .
.Задаваясь рядом значений диаметра d1, d2, …,du и вычисляя по последней формуле соответственно Q1, Q2, …, Qu, строим график Q=f(t), из которого определяем диаметр, отвечающий заданному расходу.
11.Основы подземной гидравлики.
Процессы движения жидкостей, газа и воды сквозь пористые породы изучает раздел подземной гидравлики. Расчетные модели базируются на классических положениях гидравлики, однако главной особенностью являются наличие пористой среды, поэтому законы и зависимости имеют отличия. Подземная гидравлика изучает процессы фильтрации. Основной задачей подземной гидравлики является расчет дебитов скважин и их параметров. Структура скважины представлена на рис. 4.1.
Фильтрация - движение жидкостей, газов и их смесей в пористых и трещиноватых средах, в твердых телах, пронизанной системой сообщающихся между собой пор и микротрещин.

Рис. 4.1. Схема поверхностей фильтрации в пласте с грунтовыми водами
Фильтрация жидкостей и газов по сравнению с движением в трубах и каналах обладает некоторыми особенностями, а именно происходит по чрезвычайно малым в поперечных размерах поровым каналам при очень малых скоростях движения жидкостей. При этом, поскольку площади соприкосновения жидкости с твердыми частицами при движении жидкости в пористой велики, велики и силы трения.
Пористая среда характеризуется коэффициентами пористости и просветности.
Активная пористость (пористость) - безразмерная величина, характеризующая способность пористой среды пропускать жидкость, учитывает только те поры и микротрещины, которые соединены между собой и через которые может фильтроваться жидкость.
Коэффициент пористости m - отношение объема пор (
Коэффициентом просветности n - отношение площади просветов (
Среднее по длине пласта значение просветности равно пористости, т.е.
Поэтому среднее значение площади просветов
Скоростью фильтрации
Скорость фильтрации представляет собой фиктивную скорость, с которой двигалась бы жидкость, если бы пористая среда отсутствовала (m=1), поэтому для более корректной характеристики скорости используют понятие средней скорости движения жидкости. Скорость фильтрации и средняя скорость движения связана соотношением:
В общем виде средняя скорость движения жидкости
Коэффициент фильтрации с – скорость фильтрации при градиенте давления равном единице, зависит от свойств пористой среды и от свойств фильтрующейся жидкости.
Проницаемость - способность пористой среды пропускать сквозь себя жидкости и газы, характеризуется коэффициентом проницаемости. В отличии от коэффициента фильтрации с коэффициент проницаемости k зависит от свойств пористой среды.
Коэффициент проницаемости и фильтрации связаны соотношением
Коэффициент проницаемости имеет размерность площади, а коэффициент фильтрации — размерность скорости.
На практике проницаемость нефтяных и газовых пластов измеряется единицами, называемыми дарси (Д). За единицу проницаемости 1 Д принимают проницаемость такой пористой среды, при фильтрации через образец которой площадью 1 см2, длиной 1 см при перепаде давления в 1 кгс/см2 (98100 Па) расход жидкости вязкостью 1 сП (1 мПа
Для перевода в систему СИ справедливо соотношение:
Проницаемость реальных пластов изменяется от нескольких миллидарси до нескольких дарси.