Файл: Исследование электрических свойств проводниковых материалов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 58
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
l – ширина и длина пленочного резистора соответственно.
Пример расчета удельного сопротивления проволочного резистора из манганина:
ρ= RS/ l = R (π∙(d/ 2)2) / l = 63,51∙(π∙(0,1/ 2)2)/ 1,04 = 0,480 мкОм ‧ м
d, мм – диаметр проволоки
Результаты остальных расчетов сведены в таблицу 1.
Таблица 1 – Удельного сопротивления проволочных резисторов
Пример расчета сопротивления квадрата поверхности первого материала:
R□ = Rb / l = 39,07 ‧ 2,5 / 0,2 = 488,38 Ом
Результаты остальных расчетов сведены в таблицу 2.
Таблица 2 – Сопротивление квадрата поверхности разных материалов
Таблица 3 – Зависимость сопротивлений от температуры
где αR и αl – температурные коэффициенты сопротивления и линейного расширения соответственно.
Температурные коэффициенты линейного расширения имеют следующие значения:
αl никель = 12,8 ∙ 10−6 К–1;
αl медь = 16,7 ∙ 10−6 К–1;
αl константан = 17,0 ∙ 10−6 К–1.
Температурный коэффициент сопротивления при различных температурах рассчитан по формуле (11).
где RT – сопротивление образца при данной температуре.
Пример расчета температурного коэффициента удельного сопротивления никеля при температуре T = 298 K:
αR= 1/RT‧(R2-RT)/(T-T2) = 1/19,27‧(20,08-19,27)/(313-298) = 2,802‧10-3 К–1
αρ = αR + αl = 2,802‧10-3 + 12,8 ∙ 10−6 = 2,815‧10-3 К–1
Таблица 4 – Температурные коэффициенты αR и αρ
Удельное сопротивление рассчитано по формуле (12).
где С – постоянный коэффициент;
хNi – содержание никеля в сплаве в относительных долях по массе;
Первые два слагаемых в (12) характеризуют удельное сопротивление, обусловленное рассеянием электронов на тепловых колебаниях узлов кристаллической решетки. Предполагается, что эти составляющие удельного сопротивления аддитивно зависят от состава. Третье слагаемое характеризует изменение остаточного сопротивления от состава.
Коэффициент С найден путем подстановки в формулу (12) значения удельного сопротивления константана и соответствующего ему содержания никеля хNi = 0,4. Подставляя различные значения xNi в формулу (12), получены точки для построения кривой ρ = f (x).
Значения удельного сопротивления меди, никеля и константана взяты из справочной литературы:
ρ никель = 0,068 мкОм ‧ м;
ρ медь = 0,017 мкОм ‧ м;
ρ константан = 0,5 мкОм ‧ м.
Значения температурного коэффициента удельного сопротивления сплавов Cu-Ni при различных содержаниях никеля рассчитаны с помощью формулы (13).
где CuNi − удельное сопротивление сплава соответствующего состава, определенного по (12).
Температурные коэффициенты удельного сопротивления никеля и меди взяты из таблицы 4:
αρNi = 2,815‧10-3 К-1
αρCu = 3,126‧10-3 К-1
Расчет коэффициента С:
С = (ρCu-Ni – ρNi ‧ xNi - ρCu (1-xNi))/ (xNi (1-xNi)) =
= (0,5‧10-6-0,068‧10-6‧0,4-0,017‧10-6‧(1-0,4))/(0,4‧(1-0,4))=1,9275‧10-6 Ом‧ м
Пример расчета ρCu-Ni и αρCu-Ni, при xNi= 0,2:
ρCu-Ni = ρNi ‧ xNi + ρCu (1-xNi) + СxNi (1-xNi) = 0,068‧10-6‧0,2+0,017‧10-6‧(1-
- 0,2)+1,9275‧10-6‧0,2‧(1-0,2) = 0,336 мкОм‧м
αρCu-Ni = (ρCu (1-xNi) ‧ αρCu+ xNi‧ αρNi‧ ρNi)/ρCu-Ni = (0,017‧10-6‧(1-0,2) ‧
‧ 3,126 ‧ 10-3+ 0,2‧ 2,815‧ 10-3‧ 0,068‧ 10-6)/ (0,336‧10-6) = 0,241 ‧10-3 К-1
Результаты остальных расчетов занесены в таблицу 5.
Таблица 5 – Зависимость ρ и αρ от содержания никеля в сплаве
6. По данным таблицы 5, на рисунке 3 построены зависимости удельного сопротивления сплава ρCu–Ni и температурного коэффициента удельного сопротивления сплава αρ(хCu–Ni) от состава сплава. Также на графике отмечено экспериментально найденное значение температурного коэффициента удельного сопротивления константана (Содержание никеля в константане ≈ 40%) αρ= - 4,836‧10-6 К-1.
7. Построены температурные зависимости термоЭДС ΔU(T) для исследованных термопар по данным таблицы 6. График расположен на рисунке 4.
Расчет ΔT (Tгор = 298 K):
ΔT = Tгор – Tхол = 298 – 296 = 2 К
Таблица 6 – Измеренное термоЭДС для различных термопар
Пример расчета удельного сопротивления проволочного резистора из манганина:
ρ= RS/ l = R (π∙(d/ 2)2) / l = 63,51∙(π∙(0,1/ 2)2)/ 1,04 = 0,480 мкОм ‧ м
d, мм – диаметр проволоки
Результаты остальных расчетов сведены в таблицу 1.
Таблица 1 – Удельного сопротивления проволочных резисторов
| Материал | R, Ом | l, м | d, мм | ρ, мкОм ‧ м | ρтеоретическое, мкОм ‧ м |
| Манганин | 63,51 | 1,04 | 0,1 | 0,4794 | 0,48 |
| Медь | 9,68 | 8,3 | 0,13 | 0,0155 | 0,017 |
| Нихром | 2,68 | 0,9 | 0,7 | 1,1454 | 1,12 |
| Константан | 198,57 | 1 | 0,06 | 0,5612 | 0,5 |
| Никель | 2,41 | 1,5 | 0,25 | 0,0788 | 0,068 |
Пример расчета сопротивления квадрата поверхности первого материала:
R□ = Rb / l = 39,07 ‧ 2,5 / 0,2 = 488,38 Ом
Результаты остальных расчетов сведены в таблицу 2.
Таблица 2 – Сопротивление квадрата поверхности разных материалов
| Материал | R, Ом | b, мм | l, мм | R□, Ом |
| 1 | 39,07 | 2,5 | 0,2 | 488,38 |
| 2 | 775,3 | 2 | 3,25 | 477,11 |
| 3 | 7599 | 0,6 | 9,5 | 479,94 |
-
Построены температурные зависимости сопротивления R=f (T) для исследованных резисторов. Данные, использованные для построения графика находятся в таблице 4. График изображен на рисунке 1.
Таблица 3 – Зависимость сопротивлений от температуры
| Температура | Никель | Медь | Константан |
| T, K | R, Ом | R, Ом | R, Ом |
| 298 | 19,27 | 109,78 | 30,53 |
| 313 | 20,08 | 114,9 | 30,52 |
| 328 | 22,46 | 118,35 | 30,5 |
| 343 | 22,79 | 121,94 | 30,49 |
| 358 | 24,93 | 126,1 | 30,46 |
| 373 | 24,26 | 129,98 | 30,45 |
| 388 | 27 | 133,78 | 30,45 |
| 403 | 28,83 | 137,5 | 30,42 |
| 423 | 30,43 | 142,44 | 30,4 |
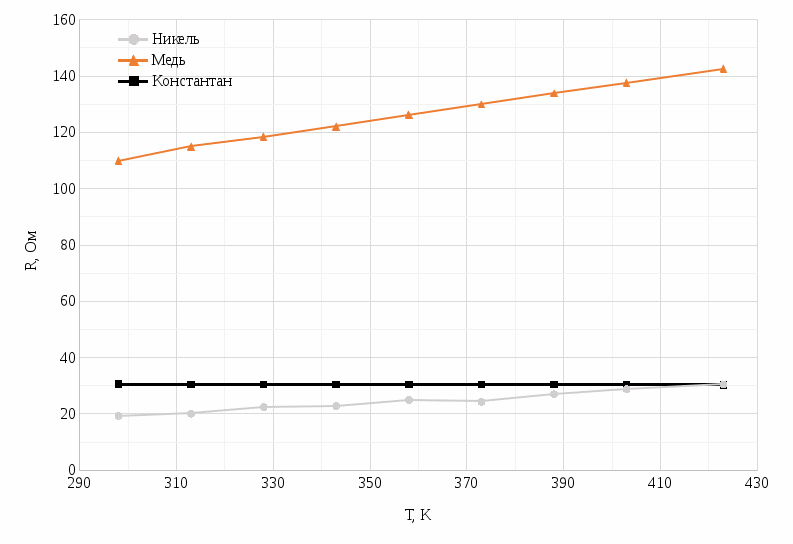 | ||
| | Рисунок 1 – Температурная зависимость сопротивления | |
-
Рассчитан температурный коэффициент удельного сопротивления металлов и сплавов по формуле (10).
| |  | (10) |
где αR и αl – температурные коэффициенты сопротивления и линейного расширения соответственно.
Температурные коэффициенты линейного расширения имеют следующие значения:
αl никель = 12,8 ∙ 10−6 К–1;
αl медь = 16,7 ∙ 10−6 К–1;
αl константан = 17,0 ∙ 10−6 К–1.
Температурный коэффициент сопротивления при различных температурах рассчитан по формуле (11).
| | 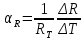 | (11) |
где RT – сопротивление образца при данной температуре.
Пример расчета температурного коэффициента удельного сопротивления никеля при температуре T = 298 K:
αR= 1/RT‧(R2-RT)/(T-T2) = 1/19,27‧(20,08-19,27)/(313-298) = 2,802‧10-3 К–1
αρ = αR + αl = 2,802‧10-3 + 12,8 ∙ 10−6 = 2,815‧10-3 К–1
Таблица 4 – Температурные коэффициенты αR и αρ
| T, К | Никель | Медь | Константан | ||||
| αR, К–1 | αρ, К–1 | αR, К–1 | αρ, К–1 | αR, К–1 | αρ, К–1 | ||
| 298 | 2,802‧10-3 | 2,815‧10-3 | 3,109‧10-3 | 3,126‧10-3 | -2,184‧10-5 | -4,836‧10-6 | |
| 313 | 7,902‧10-3 | 7,915‧10-3 | 2,002‧10-3 | 2,018‧10-3 | -4,369‧10-5 | -2,669‧10-5 | |
| 328 | 9,795‧10-4 | 9,923‧10-4 | 2,022‧10-3 | 2,039‧10-3 | -2,186‧10-5 | -4,858‧10-6 | |
| 343 | 6,260‧10-3 | 6,273‧10-3 | 2,274‧10-3 | 2,291‧10-3 | -6,560‧10-5 | -4,860‧10-5 | |
| 358 | -1,792‧10-3 | -1,779‧10-3 | 2,051‧10-3 | 2,068‧10-3 | -2,189‧10-5 | -4,887‧10-6 | |
| 373 | 7,530‧10-3 | 7,542‧10-3 | 1,949‧10-3 | 1,966‧10-3 | 0 | 1,700‧10-5 | |
| 388 | 4,519‧10-3 | 4,531‧10-3 | 1,854‧10-3 | 1,870‧10-3 | -6,568‧10-5 | -4,868‧10-5 | |
| 403 | 2,775‧10-3 | 2,788‧10-3 | 1,796‧10-3 | 1,813‧10-3 | -3,287‧10-5 | -1,587‧10-5 | |
-
Построена зависимость αρ = f (T) для исследованных материалов. Данные взяты из таблицы 4, графики изображены на рисунке 2.
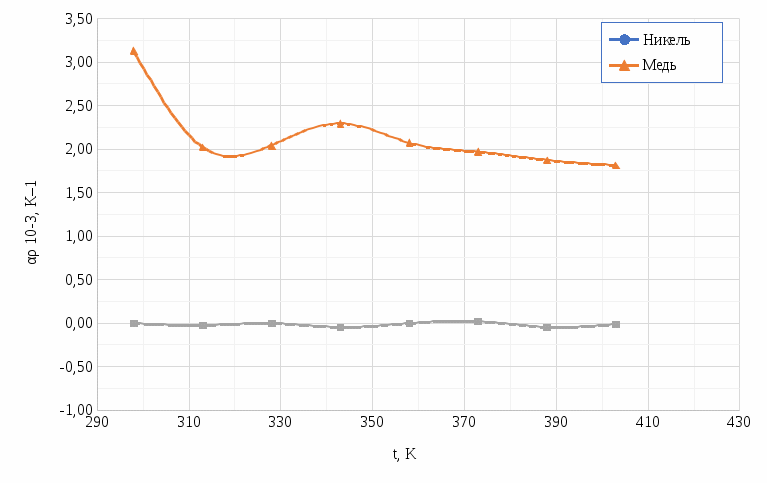 |
| Рисунок 2 – зависимости температурного коэффициента удельного сопротивления от температуры |
-
Рассчитаны зависимости удельного сопротивления и температурного коэффициента удельного сопротивления от состава для сплавов системы Cu - - Ni при комнатной температуре.
Удельное сопротивление рассчитано по формуле (12).
| |  | (12) |
где С – постоянный коэффициент;
хNi – содержание никеля в сплаве в относительных долях по массе;
Первые два слагаемых в (12) характеризуют удельное сопротивление, обусловленное рассеянием электронов на тепловых колебаниях узлов кристаллической решетки. Предполагается, что эти составляющие удельного сопротивления аддитивно зависят от состава. Третье слагаемое характеризует изменение остаточного сопротивления от состава.
Коэффициент С найден путем подстановки в формулу (12) значения удельного сопротивления константана и соответствующего ему содержания никеля хNi = 0,4. Подставляя различные значения xNi в формулу (12), получены точки для построения кривой ρ = f (x).
Значения удельного сопротивления меди, никеля и константана взяты из справочной литературы:
ρ никель = 0,068 мкОм ‧ м;
ρ медь = 0,017 мкОм ‧ м;
ρ константан = 0,5 мкОм ‧ м.
Значения температурного коэффициента удельного сопротивления сплавов Cu-Ni при различных содержаниях никеля рассчитаны с помощью формулы (13).
| |  | (13) |
где CuNi − удельное сопротивление сплава соответствующего состава, определенного по (12).
Температурные коэффициенты удельного сопротивления никеля и меди взяты из таблицы 4:
αρNi = 2,815‧10-3 К-1
αρCu = 3,126‧10-3 К-1
Расчет коэффициента С:
С = (ρCu-Ni – ρNi ‧ xNi - ρCu (1-xNi))/ (xNi (1-xNi)) =
= (0,5‧10-6-0,068‧10-6‧0,4-0,017‧10-6‧(1-0,4))/(0,4‧(1-0,4))=1,9275‧10-6 Ом‧ м
Пример расчета ρCu-Ni и αρCu-Ni, при xNi= 0,2:
ρCu-Ni = ρNi ‧ xNi + ρCu (1-xNi) + СxNi (1-xNi) = 0,068‧10-6‧0,2+0,017‧10-6‧(1-
- 0,2)+1,9275‧10-6‧0,2‧(1-0,2) = 0,336 мкОм‧м
αρCu-Ni = (ρCu (1-xNi) ‧ αρCu+ xNi‧ αρNi‧ ρNi)/ρCu-Ni = (0,017‧10-6‧(1-0,2) ‧
‧ 3,126 ‧ 10-3+ 0,2‧ 2,815‧ 10-3‧ 0,068‧ 10-6)/ (0,336‧10-6) = 0,241 ‧10-3 К-1
Результаты остальных расчетов занесены в таблицу 5.
Таблица 5 – Зависимость ρ и αρ от содержания никеля в сплаве
| xNi | 0 | 0,2 | 0,4 | 0,6 | 0,8 | 1 |
| ρ, мкОм ‧ м | 0,017 | 0,336 | 0,500 | 0,510 | 0,366 | 0,068 |
| αρ, мК–1 | 3,126 | 0,241 | 0,217 | 0,267 | 0,447 | 2,815 |
6. По данным таблицы 5, на рисунке 3 построены зависимости удельного сопротивления сплава ρCu–Ni и температурного коэффициента удельного сопротивления сплава αρ(хCu–Ni) от состава сплава. Также на графике отмечено экспериментально найденное значение температурного коэффициента удельного сопротивления константана (Содержание никеля в константане ≈ 40%) αρ= - 4,836‧10-6 К-1.
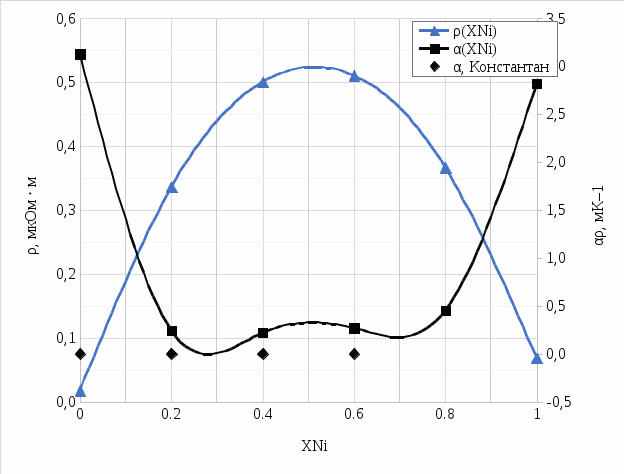 |
| Рисунок 3 – Графики зависимостей ρ и αρ от содержания никеля в сплаве |
7. Построены температурные зависимости термоЭДС ΔU(T) для исследованных термопар по данным таблицы 6. График расположен на рисунке 4.
Расчет ΔT (Tгор = 298 K):
ΔT = Tгор – Tхол = 298 – 296 = 2 К
Таблица 6 – Измеренное термоЭДС для различных термопар
| Tгор, K | Tхол, K | ΔT, K | ΔU, мВ | ||
| Медь–железо | Медь– константан | Медь– манганин | |||
| 298 | 296 | 2 | -0,13 | -0,12 | -0,08 |
| 313 | 297 | 16 | 0,5 | 0,46 | -0,05 |
| 328 | 297 | 31 | 0,88 | 0,86 | -0,04 |
| 343 | 297,8 | 45,2 | 1,24 | 1,3 | -0,03 |
| 358 | 299 | 59 | 1,69 | 1,82 | -0,01 |
| 373 | 299,3 | 73,7 | 2,09 | 2,32 | -0,005 |
| 388 | 301 | 87 | 2,47 | 2,81 | 0,02 |
| 403 | 301 | 102 | 2,88 | 3,38 | 0,03 |
| 423 | 302 | 121 | 3,35 | 4,07 | 0,04 |