Файл: Задача определение постоянной датчика Холла, концентрации и подвижности носителей тока в полупроводнике.docx
Добавлен: 05.12.2023
Просмотров: 98
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Изучение эффекта Холла в полупроводниках №18-8
Цель работы: изучение эффекта Холла.
Задача: определение постоянной датчика Холла, концентрации и подвижности носителей тока в полупроводнике.
Приборы и принадлежности: установка для изучения эффекта Холла «ФПК-08».
Техника безопасности: к работе с установкой допускаются лица, ознакомленные с ее устройством, принципом действия и знающие правила техники безопасности при работе с напряжением до 1000В.
ОБЩИЕ ПОЛОЖЕНИЯ
Для количественной характеристики электрического тока в проводниках вводятся понятия силы тока Iи плотности тока
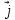 . При равномерном распределении плотности тока по сечению проводника плотность тока
. При равномерном распределении плотности тока по сечению проводника плотность тока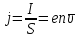 , (1)
, (1) где S – площадь поперечного сечения проводника. e – заряд носителей тока, n – их концентрация,
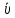 – средняя скорость направленного движения подвижных носителей (дрейфовая скорость).
– средняя скорость направленного движения подвижных носителей (дрейфовая скорость).Плотность тока
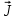 в каждой точке проводника связана с напряженностью электрического поля
в каждой точке проводника связана с напряженностью электрического поля 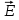 этой точке законом Ома в дифференциальной форме
этой точке законом Ома в дифференциальной форме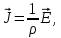 (2)
(2)где ???? – удельное сопротивление проводника.
Для однородного проводника длиной Ɩ
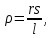 (3)
(3)где r – сопротивление этого проводника.
Если по проводнику идет ток, то на каждый подвижный носитель действует сила со стороны электрического поля Fэл ∼ Eи сила трения Fтр ∼
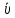 . При стационарном движении носителя (с постоянной скоростью
. При стационарном движении носителя (с постоянной скоростью 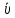 ) Fэл = Fтр следовательно,
) Fэл = Fтр следовательно, 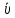 ∼ E. Коэффициент пропорциональности в этой зависимости называется подвижностью
∼ E. Коэффициент пропорциональности в этой зависимости называется подвижностью
μ, т.е.
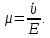 (4)
(4)Из соотношений (1), (2), (4) следует, что
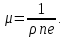 (5)
(5)Подвижность μ находит широкое применение в теории электропроводности полупроводников и металлов. К полупроводникам принято относить твердые вещества с удельным сопротивлением ???? ∽ (10-6
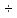 108) Ом
108) Ом м. У металлов при комнатной температуре
м. У металлов при комнатной температуре???? ∽ (10-8
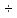 10-6) Ом
10-6) Ом м. В таблице 1 приведены характерные значения концентрации nи подвижности μ носителей тока в полупроводниках и металлах.
м. В таблице 1 приведены характерные значения концентрации nи подвижности μ носителей тока в полупроводниках и металлах. Таблица 1
| Тип твердого тела | Удельное сопротивление ????, Ом  м м | Концентрация подвижных носителей n, м-3 | Подвижность носителей тока μ, м2/Вс |
| Полупроводники | 10-6 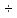 108 108 | 1019 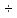 1025 1025 | 10-4 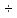 10 10 |
| Металлы | 10-8 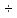 10-6 10-6 | 1028 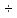 1029 1029 | 10-4 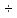 10-3 10-3 |
Интересно, что значения подвижностей тока в полупроводниках могут превышать подвижности электронов в металлах. Значительная разница удельных сопротивлений полупроводников и металлов обусловлена существенным различием в значениях концентрации свободных носителей заряда (см. формулу (5))
Во всех полупроводниках и металлах наблюдается эффект Холла, который является одним из наиболее эффективных, современных методов измерения характеристик носителей тока в этих веществах.
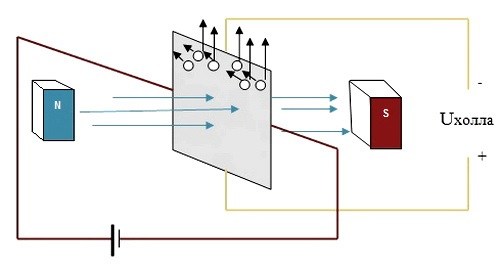
Если проводящий образец в виде прямоугольной пластины толщиной d, шириной aи длиной lпоместить в магнитное поле с индукцией
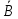 и пропустить по нему ток силой I, как показано на рис.1, то в нем появится разность потенциалов [1]
и пропустить по нему ток силой I, как показано на рис.1, то в нем появится разность потенциалов [1]
Рис. 1 Эффект Холла
 Ux= R
Ux= R 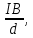 (6)
(6)где R – постоянная Холла. Этот эффект обусловлен силой Лоренца, которая действует со стороны магнитного поля на подвижные носители тока, дрейфующие в электрическом поле со скоростью
 . При этом направление этой силы не зависит от знака заряда носителей, что позволяет по знаку холловской разности потенциалов установить знак носителей тока.
. При этом направление этой силы не зависит от знака заряда носителей, что позволяет по знаку холловской разности потенциалов установить знак носителей тока.При изменении направления магнитного поля на обратное или при изменении направления тока, протекающего через образец, на обратное разность потенциалов
Ux(эдс Холла) меняет знак на противоположный.
Если основной вклад в эффект вносит один из носителей (электроны в металлах, электроны или дырки в полупроводниках), то для расчета постоянной Холлы можно пользоваться выражением
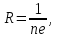 (7)
(7)где e– элементарный заряд (модуль заряда электрона).
ЭКСПЕРИМЕНТАЛЬНАЯ УСТАНОВКА И
МЕТОДИКА ЭКСПЕРИМЕНТА
Установка состоит их двух блоков (рис. 2) – измерительного блока 1 и блока с исследуемым образцом 2 (датчиком Холла).
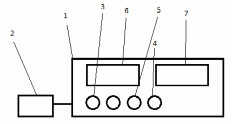
Рис. 2 Схема установки
На передней панели измерительного блока размещены следующие органы управления и индикации:
- кнопки «ТОК + -» 3, позволяющие регулировать ток через катушку электромагнита и исследуемый образец;
- кнопка «ЭЛ. МАГНИТ – ДАТЧ. ХОЛЛА» 4, с помощью которой осуществляется переход от регулировки тока датчика и регулировки тока электромагнита и обратно;
-кнопка «СБРОС» 5, после нажатия, которой значение тока обнуляется, и направление тока меняется на противоположное
;
- табло «мА» 6, которое позволяет проводить измерение тока, протекающего через катушку электромагнита, либо через датчик Холла;
- табло «мВ» 7, служащее для измерения разности потенциалов U.
На задней панели измерительного блока расположен выключатель «СЕТЬ».
В блоке 2 установлен электромагнит и датчик Холла. Сверху блок имеет окно, через которое видны полюса электромагнита и плата с датчиком Холла. Индукция магнитного поля в зазоре электромагнита определяется эмпирической формулой
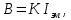 (8)
(8)где Iэм – сила тока, протекающего через электромагнит, K=2,123 Тл/А.
Датчик Холла представляет полупроводниковую пластину прямоугольной формы размерами a=31 мкм, d=35 мкм, l=42 мкм (см. Рис. 1). Сопротивление датчика r=1,8 кОм. Удельное сопротивление с учетом S=a
 d(3) может быть рассчитано по формуле
d(3) может быть рассчитано по формуле 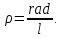 (9)
(9)При отсутствии магнитного поля в соответствии с (6) эдс Холла равна нулю. Однако вследствие различных причин (например, недостаточно точной установки выходных электродов датчика на одной эквипотенциальной поверхности) измерительный прибор может показать некоторую разность потенциалов U0 даже при B=0. При B
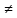 0 показания приборов, измеряющих разность потенциалов, описываются выражением
0 показания приборов, измеряющих разность потенциалов, описываются выражением 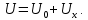
Для выделения из измеряемой разности потенциалов Uинтересующего нас холловского слагаемого Uxиспользуется тот факт, что величина Ux, в отличие от U0, изменяет знак при изменении направления магнитного поля на противоположное. Поэтому два последовательных измерения разности потенциалов U1 и U2, проведенные для обоих направлений магнитного поля, описываются соотношениями
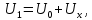
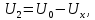
откуда следует
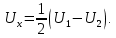 (10)
(10)В работе находится зависимость холловской разности потенциалов Ux от величины тока
Iчерез образец при заданном значении индукции B магнитного поля. В соответствии с формулой (6) эта зависимость имеет вид прямой, проходящей через начало координат (рис.3). Тангенс угла
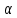 наклона этой прямой, как показывает выражение (6), есть
наклона этой прямой, как показывает выражение (6), есть 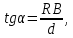
откуда
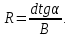 (11)
(11)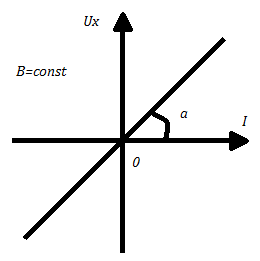
Рис. 3 Примерный вид экспериментальной зависимости
Значение постоянной Холла Rпозволяет по вытекающим из (5), (7) соотношениям
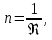 (12)
(12)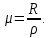 (13)
(13)В заданном значении рассчитать концентрацию nи подвижность μ носителей тока в
исследуемом полупроводнике.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
-
Величину индукции Bмагнитного поля, при которой снимается токовая зависимость Ux(I), задает преподаватель. Рекомендуемый интервал возможных значений магнитного поля (1,0 2,0) 10-2 Тл. Это значение заносится в таблицу 2.
2,0) 10-2 Тл. Это значение заносится в таблицу 2.
Таблица 2
| В, Тл | | I, мА | -2,0 | -1,5 | -1,0 | -0,5 | 0 | 0,5 | 1,0 | 1,5 | 2,0 | |
| Iэм, мА | | U1, мВ | | | | | | | | | | |
| | | | U2, мВ | | | | | | | | | |
| | | | Ux, мВ | | | | | | | | | |