Файл: Параметрлі есептерді шешуді дістсілдері.docx

5. Графиктердің қиылысу нүктелерін табыңыз



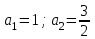
6. а=сonst түзуін жазамыз және оны - -тен +-ке дейін созамыз.

Жауап.

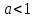болғанд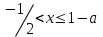а

болғанда

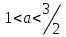болғанда,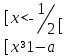

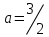болғанда, шешім жоқ

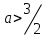болғанда,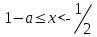

2.2. ПАРАМЕТРЛЕРІ БАР ЕСЕПТЕРДІ ШЕШУДІҢ КООРДИНАТАЛЫҚ-ПАРАМЕТРЛІК ӘДІСІ

---

Жоғарыда айтылғандай, параметр ұғымы айнымалы шама ұғымымен тығыз байланысты. Сонымен, айнымалы шама-әртүрлі мәндерді қабылдайтын шама.

Параметр-сандық мәндері белгілі бір элементті сол тектегі элементтер жиынтығынан ажыратуға мүмкіндік беретін шама.

Егер белгісіз шамадан басқа теңдеуге әріптермен көрсетілген белгісіз, бірақ тұрақты сандар кірсе, онда олар параметрлер деп аталады, ал теңдеу параметрлік деп аталады.

Мысалы: ах = 9; 2х – 7q = 8; (2а + 5)х² – ах + 3 =0.

Мұнда х — белгісіз, а және р-параметрлер.

Параметрді қамтитын теңдеуді шешу-бұл параметрдің әрбір мәні үшін берілген теңдеудің барлық түбірлерінің жиынын табу.

Бір айнымалысы бар сызықтық теңдеу деп аталатын нәрсені еске түсірейік.

Анықтама: ax = b түр теңдеуі, мұндағы x – айнымалы, a және b – кейбір сандар бір айнымалысы бар сызықтық теңдеу деп аталады.

1. 
   Параметрі бар есептерге, мысалы, жалпы түрінде сызықтық және квадрат теңдеулердің шешімін табу, параметр мәніне байланысты қол жетімді түбірлер санына теңдеуді зерттеу жатады.
   
2. 
   Параметрмен теңдеуді шешу, әдетте, теңдеулердің шексіз жиынтығын шешуді білдіреді.
   
3. 
   Егер теңдеудегі параметрге белгілі бір сандық мән берілсе, онда екі жағдайдың бірі мүмкін:
   

1. Бұл тек сандар мен белгісіз және параметрлері жоқ теңдеу болады;

2. Мағынасы жоқ шарт шығады.

Бірінші жағдайда параметрдің мәні рұқсат етілген, екіншісінде рұқсат етілмеген деп аталады. Есептерді шешкен кезде параметрлердің рұқсат етілген мәндері нақты мағынадан анықталады.

Координатно-параметрический метод. Параметрлері бар есептерді шешудің ең тиімді әдістерінің бірін қарастырыңыз-координаталық-параметрлік әдіс. Координаталық-параметрлік әдіс немесе КП әдісі-координаталық – параметрлік жазықтықты қолдана отырып, параметрлері бар есептерді шешу әдісі. Жазықтықта жалпы басталуы бар екі өзара перпендикуляр сандық ось берілсін (яғни олардың біреуі (Ох) координат деп аталады; екіншісі (Оа) параметрлік, ал жазықтық (хОа немесе аОх) координаталық параметрлік. параметр теңдеу логарифмдік есептеу Параметрі бар есептерді осы әдіспен шешкен кезде координаталық-параметрлік жазықтықтың барлық нүктелерінің жиынтығын, х координатасының мәндерін және А параметрін табу керек, олардың әрқайсысы тапсырма жағдайында берілген шартты (қатынасты) қанағаттандырады.

---

Егер көрсетілген нүктелер жиынтығы табылса, онда әрбір қол жетімді параметр мәні a= const осы жиынтықтың қажетті шешімін беретін х нүктелерінің координаттарын сәйкестендіруге немесе есептің шешімдері бар параметр мәндерін көрсетуге болады.

Параметрлері бар теңдеулердің координаталық-параметрлік әдісімен шешу. Теңдеу берілсін F(х, а) = 0 (біз оны * белгілейміз), мұнда F(х, а) - айнымалы функция х және сандық параметр а.

Екі ерекше жағдайды қарастырайық:

1. х координаттар-а параметрінің функциясы:

х = f(а)

Көлденең параметрлік осі бар ХОа координаталық-параметрлік жазықтығында Оа барлық нүктелердің жиынтығы, х координатасының мәндері және ( * ) теңдеуін қанағаттандыратын а параметрі-функция аргументінің рөлі параметр ойнайтын функцияның графигі.

2. а параметр-х координатасының функциясы:

а = f(х)

Бұл жағдайда Оа тік параметрлік осі бар aОХ координаталық-параметрлік жазықтығын қарастыруға және ( * ) теңдеуді қанағаттандыратын барлық нүктелердің жиынтығын, координаталық мәндерді және параметрлерді түсіндіруге болады.функция графигі мұндағы функция аргументінің рөлін координат ойнайды.

Қарастырылып отырған координаталық-параметрлік әдісте (*) теңдеуімен анықталған координаталық-параметрлік жазықтықтың барлық нүктелерінің жиынын табу орталық орын алатынын атап өткен жөн.

(*) теңдеуінің сол жағы бірінші немесе екінші дәрежелі көпмүшелер болған кезде қарапайым болады.

Сонымен, аналитикалық геометрия курсында түрдің теңдеулері дәлелденді

Р(х, а) = 0,

Мұнда Р(х,а) – екінші дәрежелі көпмүше салыстырмалы х және а, координаталық-параметрлік жазықтықта сызықтарды анықтайды: эллипс, гипербола, парабола немесе жұп түзулер (қиылысатын, параллель немесе бір-біріне біріктірілген).

Мысалы, координаталық параметрлік жазықтықта ХОа теңдеулер

,

,



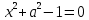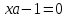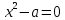
шеңбер, гипербола және парабола сәйкесінше анықталады, ал теңдеу



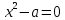
қиылысатын (өзара перпендикуляр ) түзулердің жұбын анықтайды.

"Ішінара аймақтар"әдісі. Бір айнымалы теңсіздіктерді шешуге арналған "интервалдар" әдісінің аналогы болып табылады.

Қарастырылып отырған әдіске сәйкес келетін тапсырмалардың жалпы белгілері:

---

• 
  Есепте бір параметр а және бір х айнымалы берілген;
  
• 
  Олар кейбір аналитикалық өрнектерді құрайды F(x;a), G(x;a)
  
• 
  F(x;a)=0,G(x;a)=0 теңдеулер графиктері, олар оңай салынады.
  

Енді облыстық әдіспен шешудің барлық қадамдарын егжей-тегжейлі қарастырайық.

Мысалы. Теңсіздік берілсін Р (х,а) > 0, (1)

Мұнда Р (х ,а) – көпмүшелік, оның аргументтері айнымалы х және апараметр болып табылады.

Теңдеу болсын

Р (х,а) =0

координаталық-параметрлік жазықтықтағы кейбір сызықтарды анықтайды.

Осы сызықтармен координаталық жазықтықты ақырлы санға бөлейік n «ішінара аймақтар» G1,G2,…….Gn, сызықтармен шектелген Р=0.

"Ішінара аймақтардың" әрқайсысында Gi(i=1,2,…….., n) көпмүшелік Р(х,а) нөлден ерекшеленеді, өйткені ондағы нүктелер Р (х,а) =0 осы "ішінара аймақтардың" шекарасына жатады.

Әділ теорема: Әр облыста Gi(i=1,2,…….., n), сызықтар Р=0 КП-жазықтықты, көпмүшені бөліңіз Р (х,а) не оң, не теріс.

Осылайша, теңсіздікті шешу (1) - теңсіздік орындалатын (X,a) сандарының барлық жұптарының жиынтығы сол аймақтардың жиынтығын құрайды Gi(i=1,2,…….., n), онда мағынасы Р (х,а) оң.

Теңсіздіктердің қайсысы екенін анықтау үшін Р>0 немесе P<0 бұл салада орындалады, мәнді есептеу жеткілікті Р (х,а) осы аймақтың белгілі бір нүктесінде.

Теңсіздік Р (х,а) < 0 сол сияқты шешіледі.

Алгебралық теңсіздіктер жүйесін шешу



ол орындалатын аймақтар жүйесінің теңсіздіктерінің әрқайсысы үшін іздеуден және осы аймақтардың барлығының қиылысын табудан тұрады.

P(x, a) > 0 түрдің теңсіздігі берілсін. Бұл түр үшін координаталық-параметрлік әдіс негізінде шешім алгоритмін тұжырымдаймыз:

1) рұқсат етілген мәндер аймағын координаталық-параметрлік жазықтықта табыңыз (айнымалы және параметрдің рұқсат етілген мәндерінің аймағы).

2) Координаталық-параметрлік жазықтықта барлық нүктелерден тұратын, х координатасы мен а параметрінің мәндері бар сызықтар құрыңыз, олардың әрқайсысында өрнек бар P(х,а) нөлге айналады немесе жоқ.

3) Осы сызықтармен табылған рұқсат етілген мәндер аймағын "ішінара аймақтарға"бөліңіз.

4) Өрнек белгісін зерттеу P(х,а) алынған жеке облыстардың әрқайсысында. Ол үшін өрнек белгісін қою жеткілікті P(х,а) "жеке аймақтардың"әрқайсысында бір нүктеде.

5) Жауап ретінде өрнек "ішінара аймақтардан" жазылады P(x,a) оң. Теңсіздік P(x,a) < 0 сол сияқты шешіледі.

---

Координаталық жазықтық. Параметрге есепте қандай рөл берілгеніне байланысты (айнымалымен тең емес немесе тең), сәйкесінше екі негізгі графикалық техниканы ажыратуға болады: координаталық жазықтықта Графикалық кескін салу (X;Y), екіншісі (Х;а) немесе (а,Х).

Жазықтықта (X;Y) функция у=f(х,а) а параметріне байланысты қисықтар тобын анықтайды.
0>

---