ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 189
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Xoa координаталық-параметрлік жазықтығында алынған теңсіздіктер жүйесінің шешімі x > 0 сәулесінен a = 0, ал A > 0 кезінде x = 0 параметрлік осінің нүктелері жоқ тоқсанның барлық I нүктелерінен тұратын жиын болып табылады, сондай-ақ бұрыш нүктелері
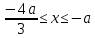 , x = -a. 12-суретте бұл жиынтық штрихталған. Жауап: Егер a < 0, онда шешімі жоқ; егер a = 0, онда x > 0; егер a > 0, онда
, x = -a. 12-суретте бұл жиынтық штрихталған. Жауап: Егер a < 0, онда шешімі жоқ; егер a = 0, онда x > 0; егер a > 0, онда 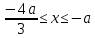 және x > 0.
және x > 0.Показательные и логарифмические уравнения и неравенства с параметрами
12. Қандай мәндерде а теңдеу
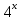 - (a + 2)*
- (a + 2)*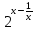 + 2a *
+ 2a * 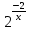 = 0 дәл екі шешім бар ма?
= 0 дәл екі шешім бар ма?Шешім: теңдеудің екі бөлігін де көбейту арқылы (x ≠ 0)
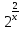 ≠ 0:
≠ 0: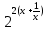 - (a+2)*
- (a+2)*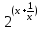 + 2a = 0 ;
+ 2a = 0 ; 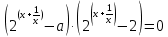 ;
;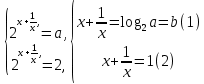
(1) теңдеу жиынға x ≠ 0,
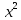 – bx + 1 = 0 квадрат теңдеуге тең, егер оның дискриминанты оң болса, оның екі шешімі бар
– bx + 1 = 0 квадрат теңдеуге тең, егер оның дискриминанты оң болса, оның екі шешімі барD =
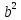 - 4 > 0 ; |b| > 2 ; |
- 4 > 0 ; |b| > 2 ; |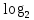 a| > 2 ;
a| > 2 ; 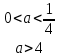
(2) теңдеудің нақты шешімдері жоқ.
ХОУ координаталық-параметрлік жазықтығында (x; b) барлық нүктелер жиыны, координаталық мәндер және олардың әрқайсысының параметрлері (1) теңдеуін қанағаттандырады,
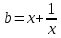 функцияның графигі болып табылады, тікелей графиктерді қосу арқылы алынған b = x және
функцияның графигі болып табылады, тікелей графиктерді қосу арқылы алынған b = x және 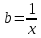 гиперболасы.
гиперболасы. 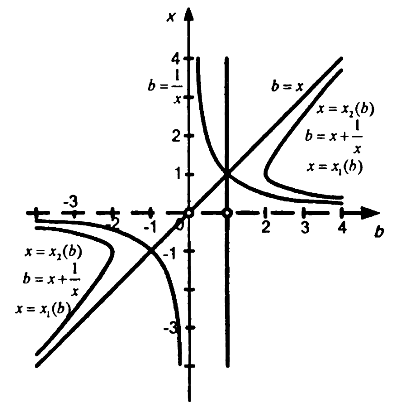
Сурет-13
Сондықтан b < -2 (0 < а < 1/4) және b > 2 (a>4) тең болғанда, (1) теңдеуінің тура екі шешімі бар, өйткені түзу
b = const бұл жағдайда функцияның графигі (3) екі нүктеде қиылысады. b = 1 кезінде (1) - ден алынған (2) теңдеудің шешімдері жоқ.
Жауабы: 0 < a <
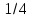 , a > 4.
, a > 4.13. Теңдеуді шешіңіз
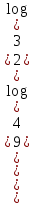 а параметрінің әрбір мәні үшін.
а параметрінің әрбір мәні үшін.Шешім: негіздерді теңестіріңіз:
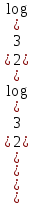
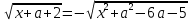
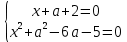
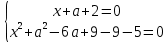
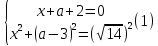
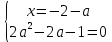
Әрі қарай, сіз екі жүйеден тұратын жиынтық жасай аласыз:
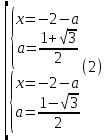
XОa координаталық-параметрлік жазықтығында (1) теңдеулер жүйесінің шешімі
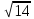 радиус шеңберімен түзудің қиылысу нүктелерімен бейнеленген және центрі x = 0 және a = 3 нүктелерінде, ал жүйелер жиынтығының шешімі (2) түзу жұптардың қиылысатын екі нүктесімен бейнеленген (14-сурет)
радиус шеңберімен түзудің қиылысу нүктелерімен бейнеленген және центрі x = 0 және a = 3 нүктелерінде, ал жүйелер жиынтығының шешімі (2) түзу жұптардың қиылысатын екі нүктесімен бейнеленген (14-сурет)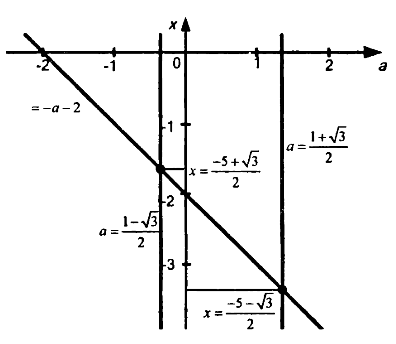
Сурет - 14
Жауап: Егер
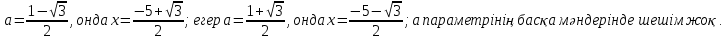
14. Теңсіздікті шешіңіз
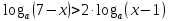 әрбір рұқсат етілген мән үшін а.
әрбір рұқсат етілген мән үшін а.Шешім: рұқсат етілген мәндер аймағын ескере отырып, жүйені құрайық:
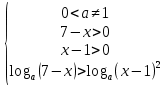
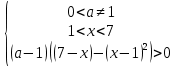
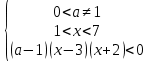
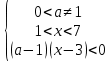
XОа координаталық-параметрлік осіне барлық нүктелердің жиынын, x координатасының мәндерін және а параметрін салайық, олардың әрқайсысы алынған жүйені қанағаттандырады (15-суретте бұл жиын штрихталған).
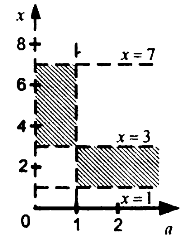
Сурет-15
Жауап: Егер
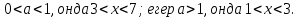
15. Теңсіздікті шешіңіз
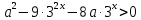 барлық мәндер үшін а.
барлық мәндер үшін а.Шешім: Жүйені құрайық:
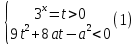
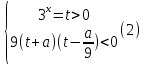
tOa координаталық-параметрлік жазықтығында t > 0 теңсіздігі жоғарғы жартылай жазықтықты көрсетеді(параметрлік осі жоқ t = 0).
Түзу сызықтар t = -a және t =
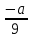 жазықтықты төрт жартылай аймаққа бөліңіз (I-IV). Осы сызықтар бойымен теңсіздіктің сол жағы нөлге айналады, ал олардың арасында белгі сақталады: I және III облыстарда оң, II және IV – де теріс (координаталық-параметрлік жазықтықта теңсіздіктің шешімін анықтайды (2)).
жазықтықты төрт жартылай аймаққа бөліңіз (I-IV). Осы сызықтар бойымен теңсіздіктің сол жағы нөлге айналады, ал олардың арасында белгі сақталады: I және III облыстарда оң, II және IV – де теріс (координаталық-параметрлік жазықтықта теңсіздіктің шешімін анықтайды (2)).Жазықтықтағы (1) және (2) теңсіздік жүйелерін шешу – T > 0 жартылай жазықтығының II және IV аймақтармен қиылысуы (16-суретте бұл жиын көлеңкеленген).
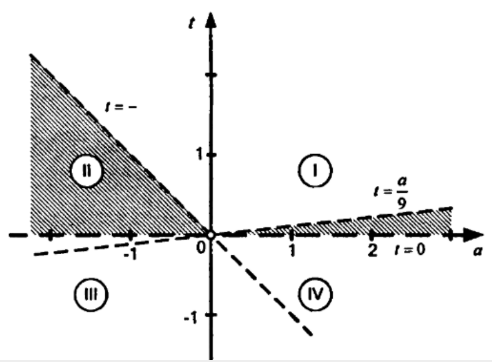
Сурет 16
Біз қарастырылып отырған жүйенің шешімін a әр мәні үшін жазамыз және қолданылатын алмастыруды қолданамыз:
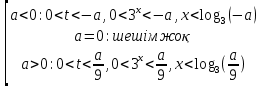
Жауабы:
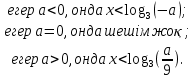
Тригонометрические уравнения и неравенства с параметрами.
16. а параметрінің қандай мәндерінде теңдеу болады
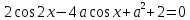 ?
?Шешім: есіңізде болсын
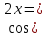 2cos2x – 1.
2cos2x – 1.4cos2x – 2 - 4a∙
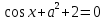 ;
;4cos2x – 4a∙
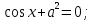
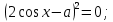
2
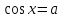 .
.Алынған тригонометриялық теңдеудің |a| > 2параметрдің барлық мәндерінде нақты түбірлер болмайды.
17-суретте тік параметрлік осі бар aОХ координаталық-параметрлік жазықтықтағы шешім көрсетілген.
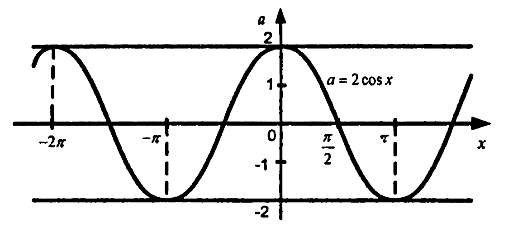
Сурет 17
17. Теңдеуді шешіңіз
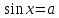 аралыққа жататын а параметрінің әрбір рұқсат етілген мәні үшін [
аралыққа жататын а параметрінің әрбір рұқсат етілген мәні үшін [
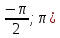 .
.Шешім: 18-суретте тік параметрлік осі бар координаталық-параметрлік жазықтықта шешім көрсетілген.
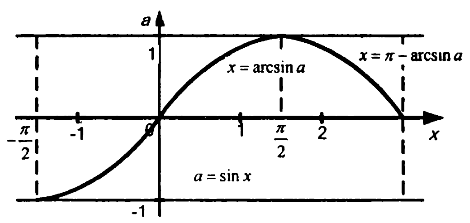
Сурет - 18
Жауабы: Егер
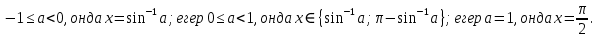
18. Әрбір параметр мәні үшін a ≠ 0 теңсіздікті шешіңіз
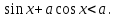
Шешім: теңсіздікті баламалы жүйемен ауыстырыңыз:
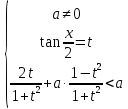
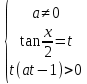
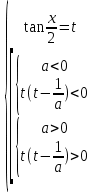
19-суретте жүйелер жиынтығының шешімі көрсетілген.
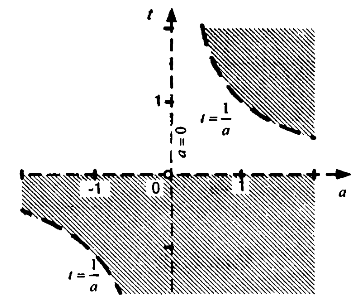
Сурет - 19
Сондықтан, егер
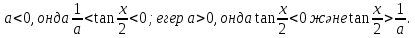
Біз қарапайым тригонометриялық теңсіздіктерді шешеміз және жауап аламыз.
Жауабы: Егер
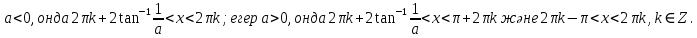
-
2.3. ПАРАМЕТРЛІ ИНТЕРВАЛДАР ӘДІСІМЕН БӨЛШЕК-РАЦИОНАЛДЫ ТЕҢСІЗДІКТЕРДІ ШЕШУ
Интервал әдісі. Интервал әдісі, ең алдымен, функцияның нөлдерін немесе оның аралықтарын табу мәселелерімен байланысты математикалық қызметтің маңызды әдістерінің бірі болып табылады.теңсіздік үшін тұрақтылық белгісі. Сондай-ақ, интервал әдісі функцияларды зерттеу және график құру мәселелерінде өте тиімді және маңызды. Бұл функция графигінің асимптотикалық өзгеруін анықтаған кезде, экстремумның нүктелері мен түрлерінің орналасу мәселелерінде, сондай-ақ функцияның монотондылығының аралықтарында кездеседі. Дәл осы әдіс әр түрлі мәселелерді шешуде тиімдірек, онсыз күрделі теңсіздіктерді шешу мүмкін емес. Оны түсінудің қарапайымдылығы мен практикалық қолданудағы тиімділігін де ескеру қажет.
Интервал әдісі қолданылған кезде бірнеше ескертулерді ескеру қажет.
Ескерту 1, интервал әдісі көпмүшелік немесе бөлшек өрнек нөлмен салыстырылған кезде ғана қолданылады.
Ескерті 2, екінші кезекте көбейткіштерге бөлінеді: көпмүше немесе бөлшек өрнектің алымы мен бөлгіші.
Ескерту 3, егер теңсіздік канондық түрге келтірілсе, онда оң жақ аралықта "+"белгісі болады. Теңсіздіктің канондық түрі-бұл әр түрлі биномдардың және "ашылмайтын" көпмүшелердің көбейтіндісі, онда үлкен коэффициент оң болады.
Теңсіздікті интервал әдісімен шешудің бірнеше әдісі бар:
I) 3х - 5>10 – сызықтық теңсіздік. Тасымалдау шешімі: 3х>15,онда х>5, және т.б.
II) х2>0 сандар арқылы шешуге болады.
III) Неғұрлым күрделі теңсіздіктер ( бөлшек, рационал және т. б.)
Рационалды теңсіздік.
Анықтама 1: Х-қа қатысты рационалды өрнектері бар сол және оң жақтағы теңсіздіктер белгісіз х-пен рационалды теңсіздік деп аталады.
Мысалы:
(5x+1)(3-2x)<0
(4x-6/5-x)>2
Анықтама 2. Белгісіз х - пен теңсіздіктің шешімі-бұл теңсіздікке ауыстырылған кезде х орнына дұрыс сандық теңсіздік пайда болатын сан,х орнына дұрыс сандық теңсіздік алынады.
Теңсіздікті шешу-оның барлық шешімдерін табу немесе олардың жоқтығын көрсету.
x-x0<0 x-x0>0
Түрдің теңсіздіктерін шешуге арналған интервал әдісі A(x)<0 және A(x)>0 және келесі тұжырымға негізделген x0 нүктесі Ox осін екі бөлікке бөледі:
1) х0 нүктесінің оң жағындағы кез келген x үшін х-x0 биномы оң болады;
2) х0 нүктесінің сол жағында орналасқан кез келген x үшін х-x0 биномы теріс болады.
Теңсіздікті шешу қажет болсын
(X-
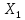 ) (X-
) (X-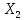 )∙…∙(X-
)∙…∙(X-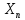 )>0; біз қоямыз
)>0; біз қоямыз(X-
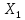 )(X-
)(X-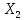 )(X-
)(X-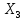 )(X-
)(X-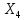 )>0 Сонда:
)>0 Сонда:Сол сияқты, біз келесі теңсіздікті аламыз (X-
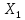 )(X-
)(X-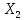 )(X-
)(X-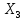 )(X-
)(X-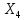 )>0
)>0X үшін интервалдардан, және (
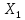 ;∞), (
;∞), (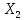 ;
;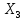 ), (-∞;
), (-∞;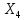 );
);(X-