ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 165
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
n различных элементов называются выборки, отличающиеся только составом самих элементов. Число 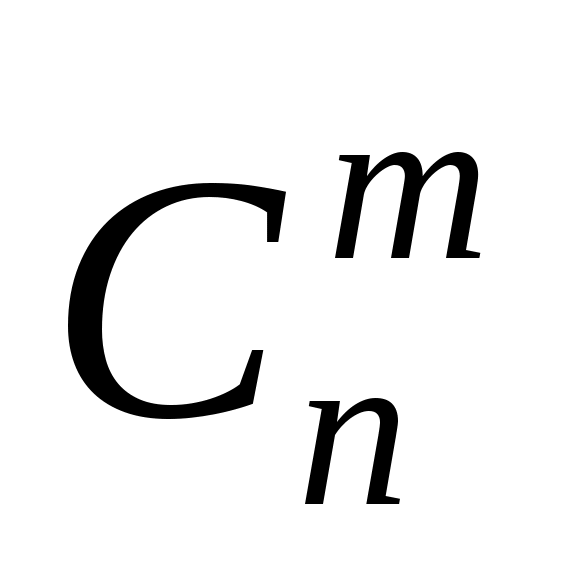 таких сочетаний находится по формуле:
таких сочетаний находится по формуле:
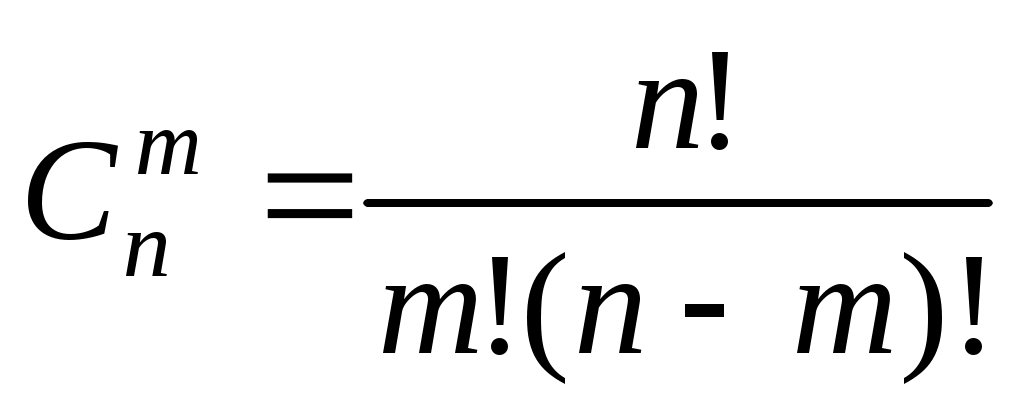 .
.
Пример 1. Игральную кость бросают один раз. Найти вероятность появления четного числа очков.
Решение. При подбрасывании одной игральной кости пространство элементарных событий (число выпавших очков) состоит из шести исходов: Ω = {1, 2, 3, 4, 5, 6}. Пусть A – событие, состоящее в появлении четного числа очков. В этом случае событию А благоприятствуют исходы выпадения 2, 4, 6 очков, т.е.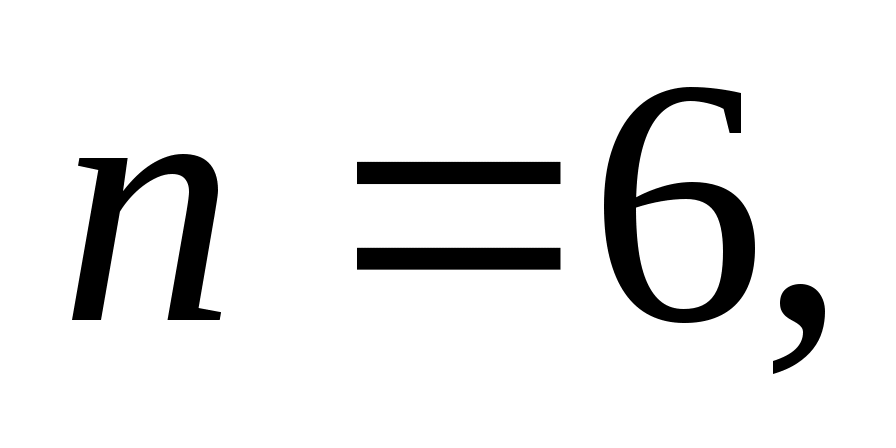
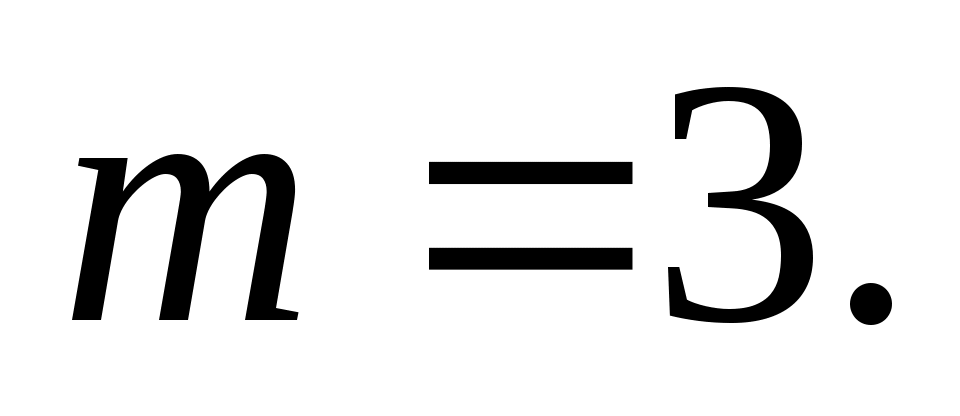 тогда
тогда
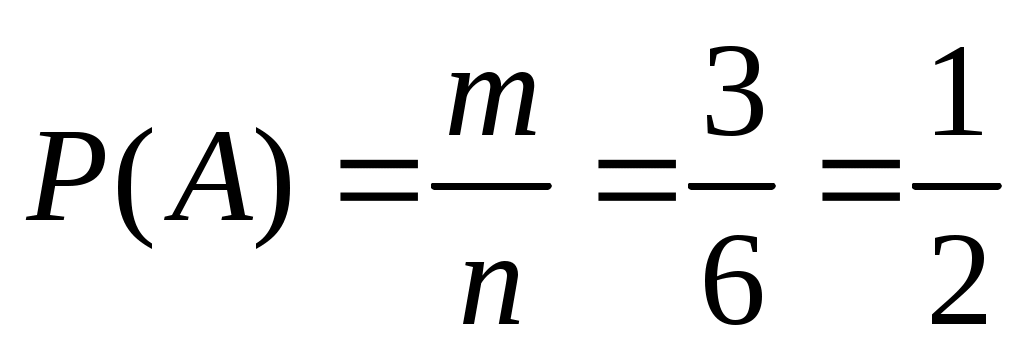 .
.
Пример 2. В ящике пять белых и четыре черных шара. Из ящика вынимают три шара. Какова вероятность того, что эти шары белые? Какова вероятность того, что один шар белый?
Решение. Пусть событие A состоит в извлечении трех белых шаров. Общее число исходов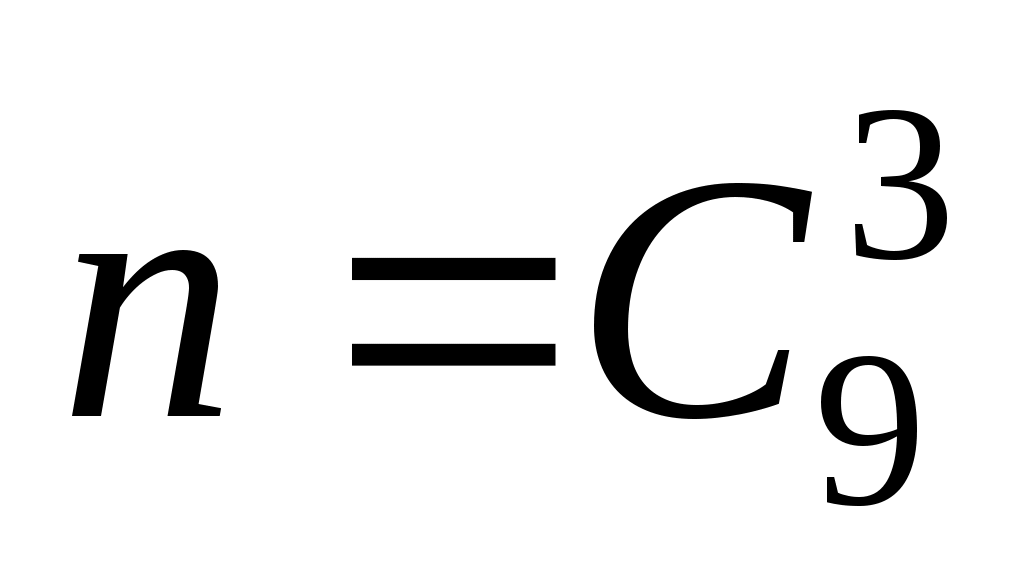 (столько различных выборок по три шара можно составить из имеющихся в ящике девяти шаров). Число m исходов опыта, благоприятных A, равно
(столько различных выборок по три шара можно составить из имеющихся в ящике девяти шаров). Число m исходов опыта, благоприятных A, равно 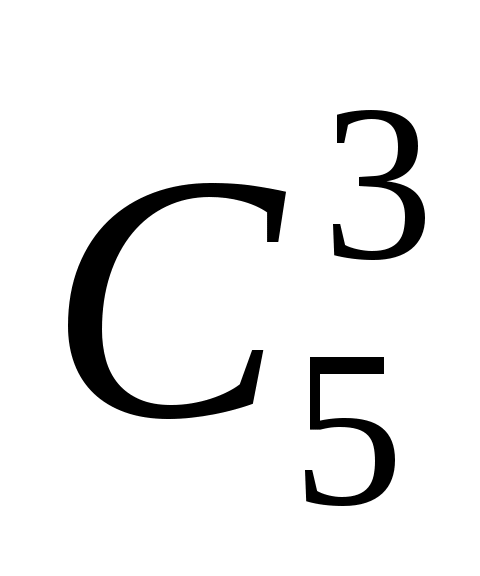 (
(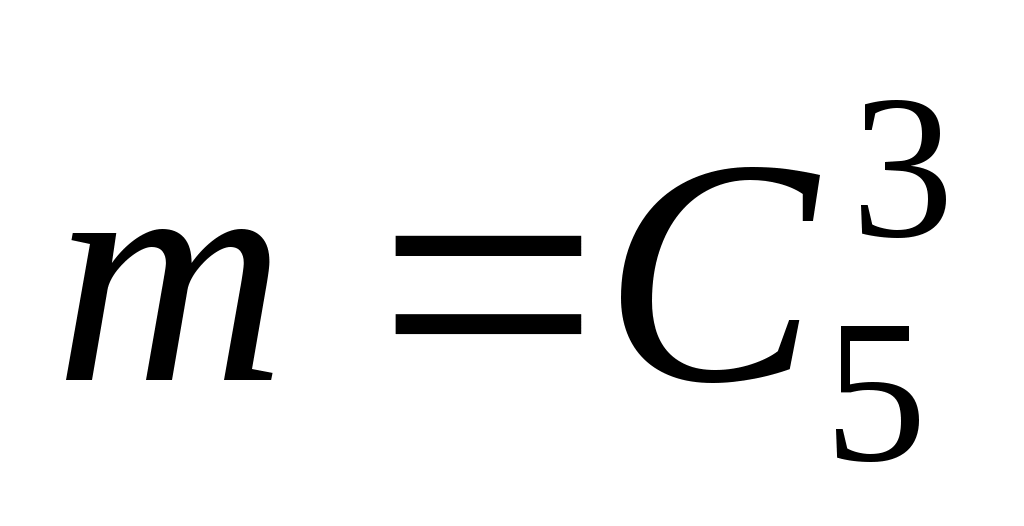 ), так как столько различных выборок по три шара можно составить из имеющихся пяти белых шаров.
), так как столько различных выборок по три шара можно составить из имеющихся пяти белых шаров.
Тогда
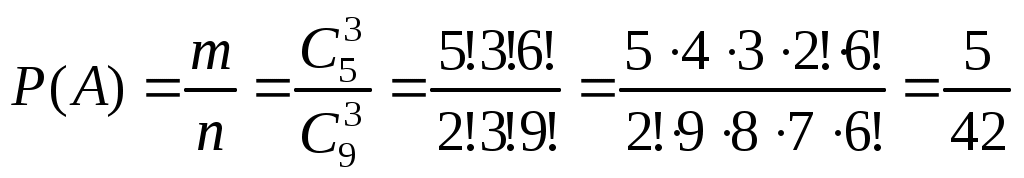 .
.
Пусть событие B состоит в извлечении трех шаров, один из которых – белый. Этот шар можно вынуть способами из пяти белых, а оставшиеся 3 – 1 = 2 шара выборки можно вынуть
способами из пяти белых, а оставшиеся 3 – 1 = 2 шара выборки можно вынуть
 способами из четырех черных шаров. Тогда число выборок, благоприятных B, определяется комбинированием всех этих способов заполнения выборки, т.е.
способами из четырех черных шаров. Тогда число выборок, благоприятных B, определяется комбинированием всех этих способов заполнения выборки, т.е. 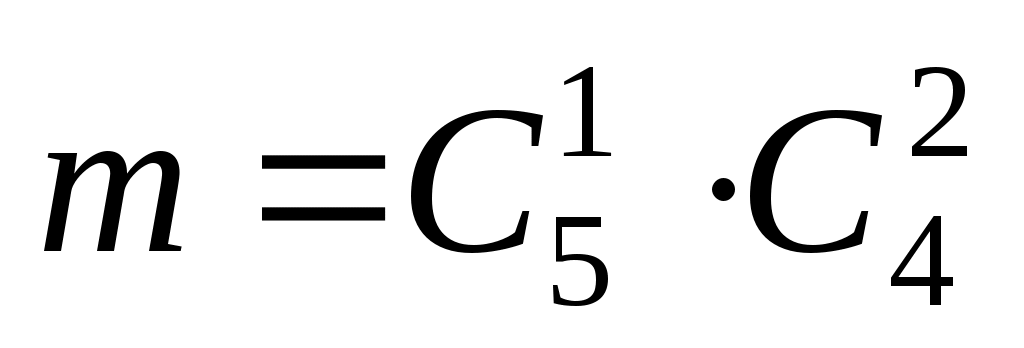 . Откуда
. Откуда
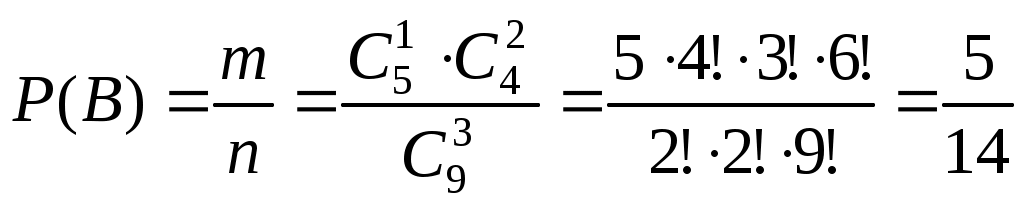 .
.
Суммой A+ B двух случайных событий A и B называется событие, состоящее в появлении события A или события B,или обоих этих событий.
Произведением AB двух событий A и B называется событие, состоящее в совместном появлении события Aи события B.
Противоположным по отношению к событию A называется событие , происходящее всегда, когда не происходит A.
, происходящее всегда, когда не происходит A.
Вероятность суммы совместных событий
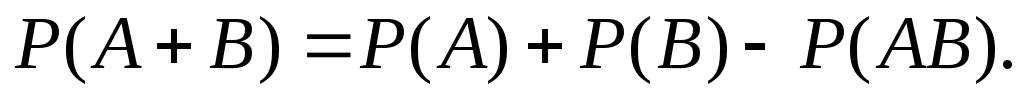
Если события A и B несовместны, то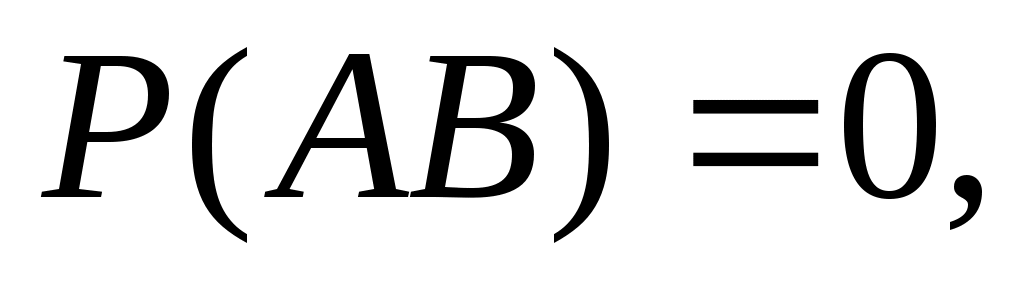 следовательно,
следовательно,
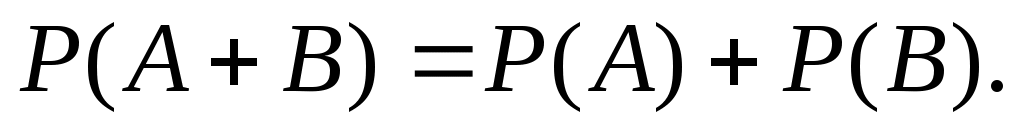
Так как противоположные события несовместны и образуют полную группу, то сумма их вероятностей
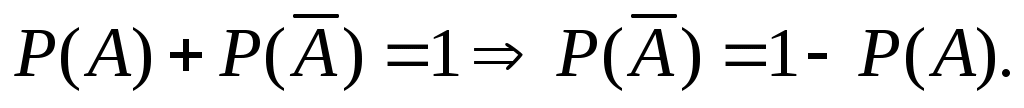
Условное событие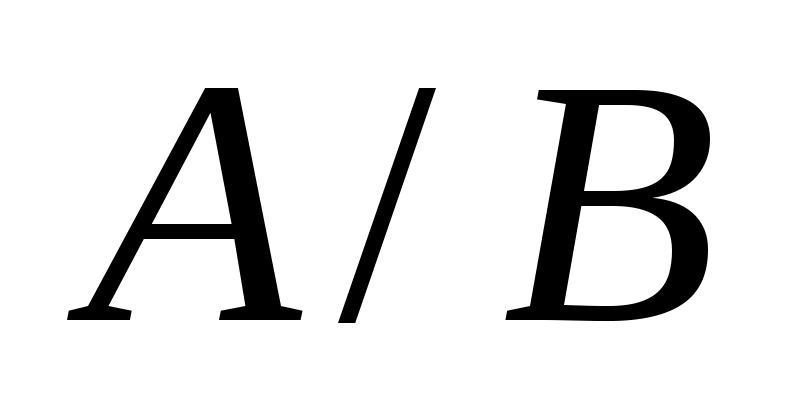 – это событие A при условии, что событие B уже произошло.
– это событие A при условии, что событие B уже произошло.
Вероятность произведения событий

где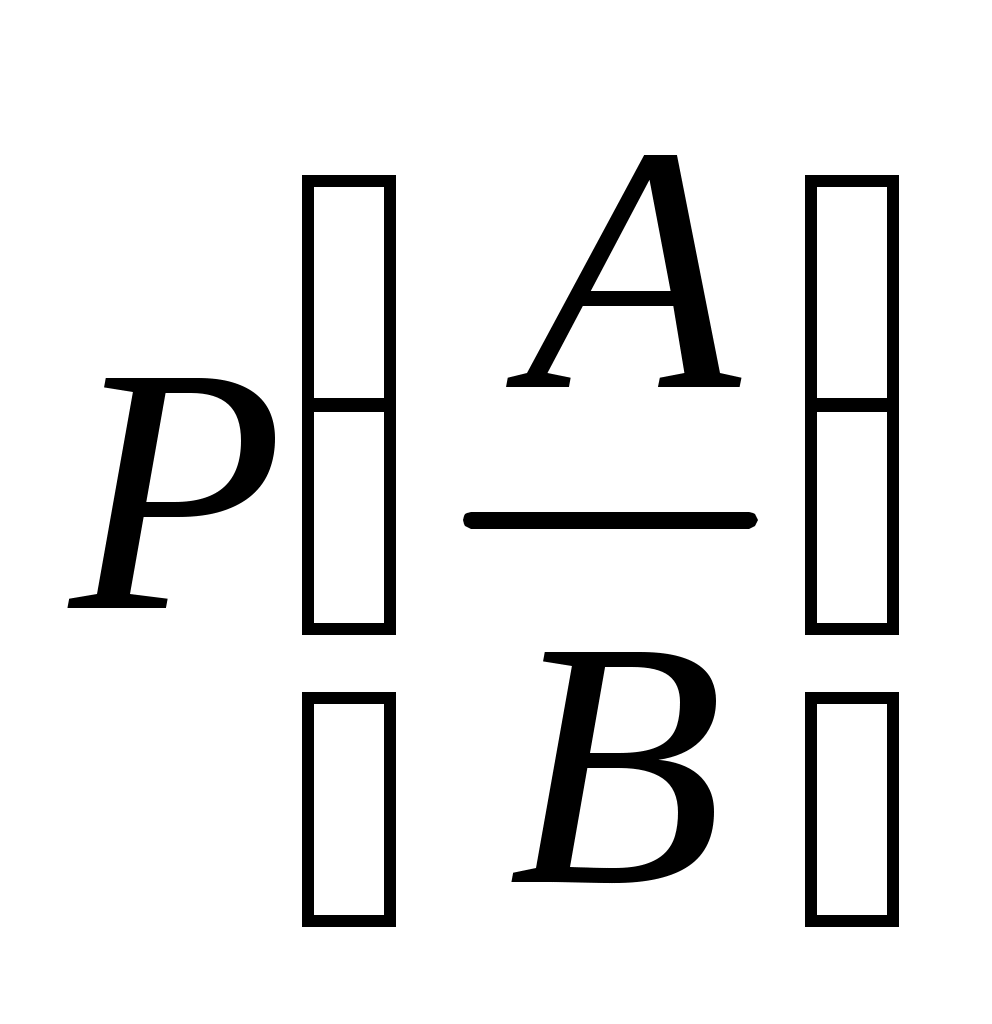 и
и 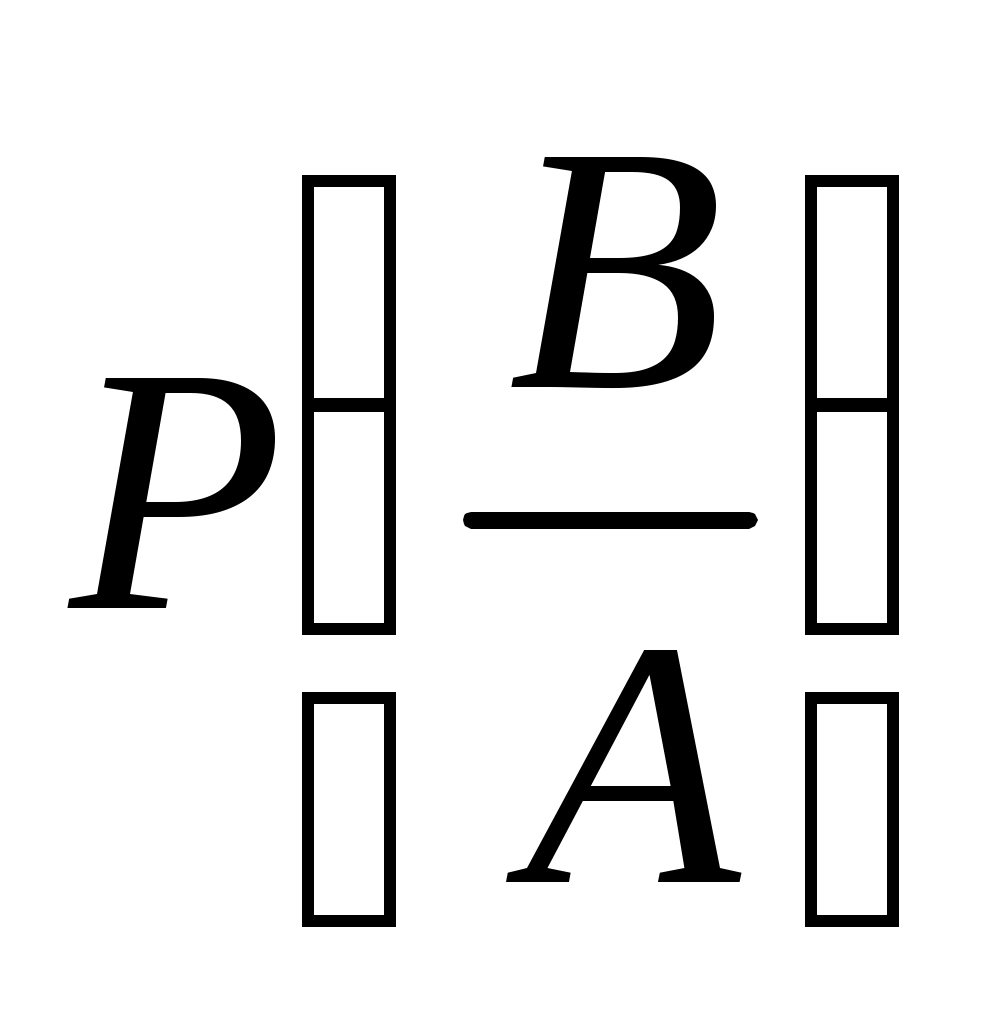 – вероятности условных событий.
– вероятности условных событий.
Если события Aи B независимы,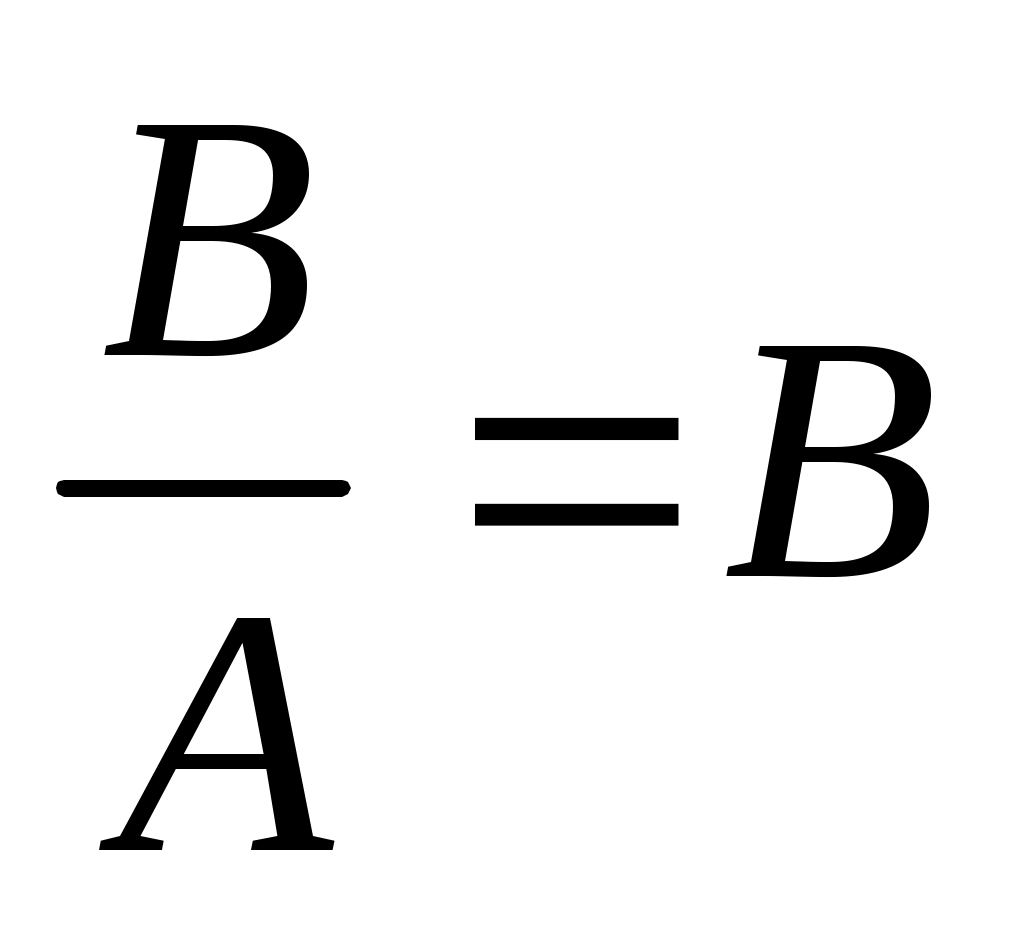 ,
, 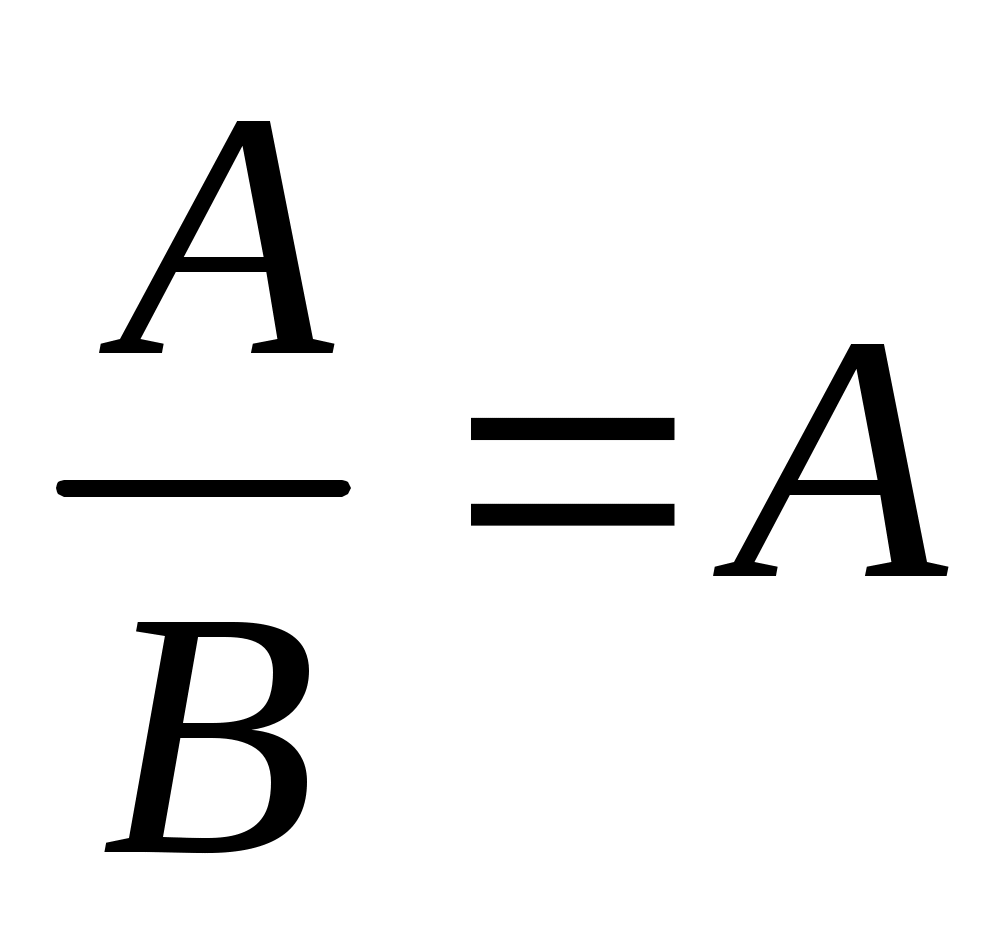 , и имеет место формула
, и имеет место формула
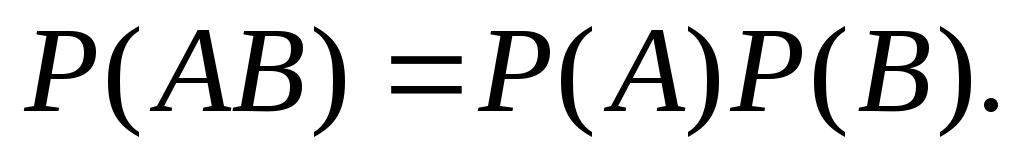
Пример 3. Разрыв электрической цепи происходит при выходе из строя двух элементов
A и B или двух элементов C и D. Найти вероятность разрыва цепи, если элементы выходят из строя независимо друг от друга с вероятностями 0,3 и 0,6, 0,4 и 0,5 соответственно.
Решение. Если события A, B, C, D – выход из строя соответствующих элементов, то по определению произведения и суммы событий согласно условию задачи разрыв цепи есть событие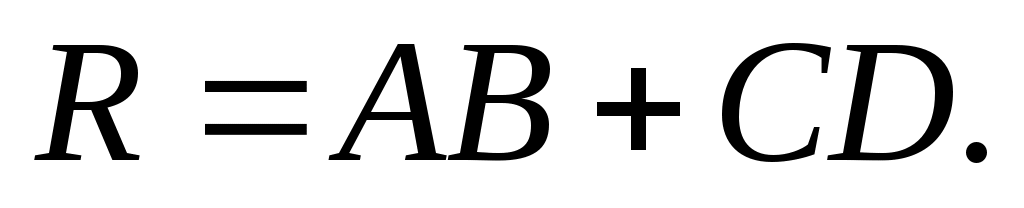
События A, B, C, Dнезависимы, но могут быть совместными, и следовательно,
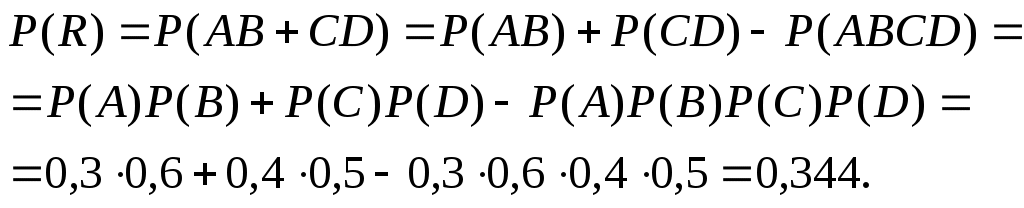
 Пример 4. Два стрелка попадают в мишень с вероятностями соответственно 0,6 и 0,8. Какова вероятность того, что после залпа в мишени будет одна пробоина? Какова вероятность, что в мишени будет хотя бы одна пробоина?
Пример 4. Два стрелка попадают в мишень с вероятностями соответственно 0,6 и 0,8. Какова вероятность того, что после залпа в мишени будет одна пробоина? Какова вероятность, что в мишени будет хотя бы одна пробоина?
Решение. Если – попадание первого стрелка,
– попадание первого стрелка,  – попадание второго стрелка, то после залпа (совместная стрельба) в мишени будет одна пробоина от кого-то одного и промаха другого стрелка, т.е.
– попадание второго стрелка, то после залпа (совместная стрельба) в мишени будет одна пробоина от кого-то одного и промаха другого стрелка, т.е. 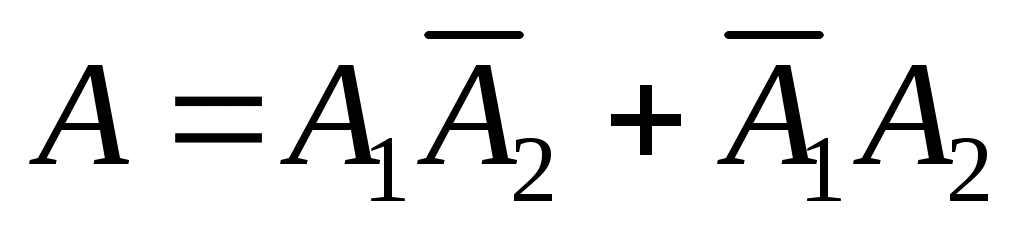 , где слагаемые, очевидно, несовместны, а попадания или промахи стрелков независимы. Поэтому, используя формулу вероятности противоположного события, получим
, где слагаемые, очевидно, несовместны, а попадания или промахи стрелков независимы. Поэтому, используя формулу вероятности противоположного события, получим
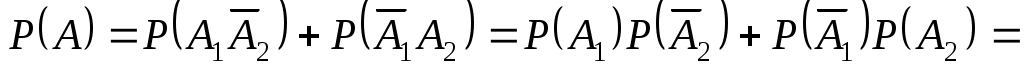
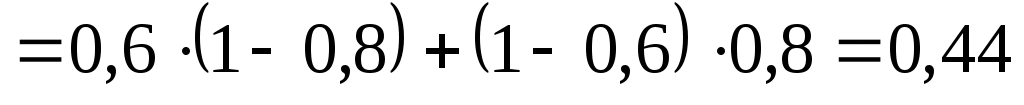 .
.
Пусть событие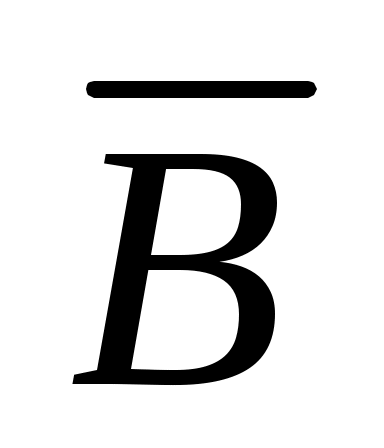 = (хотя бы одна пробоина); тогда противоположное ему событие
= (хотя бы одна пробоина); тогда противоположное ему событие 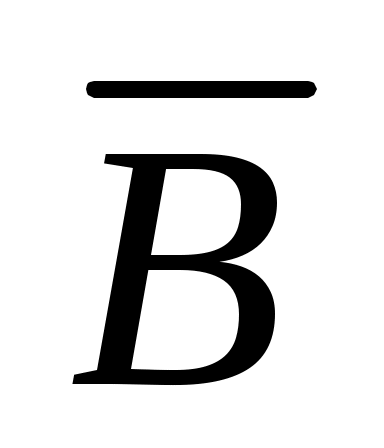 = (ни одной пробоины), т.е.
= (ни одной пробоины), т.е. 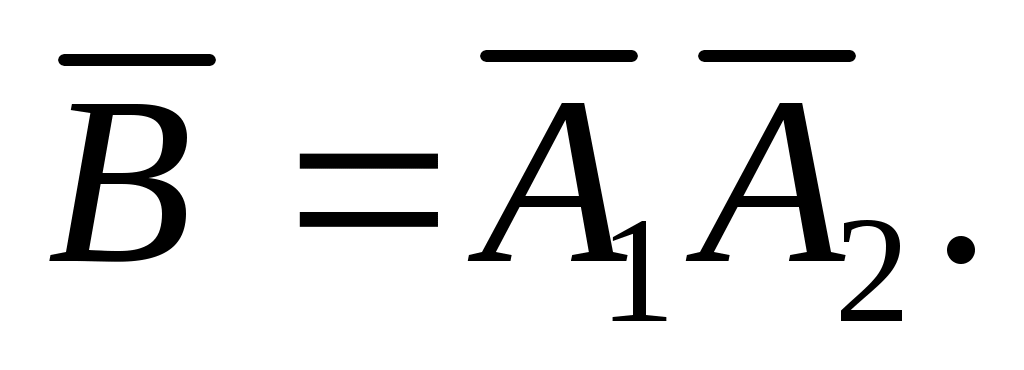 Так как
Так как 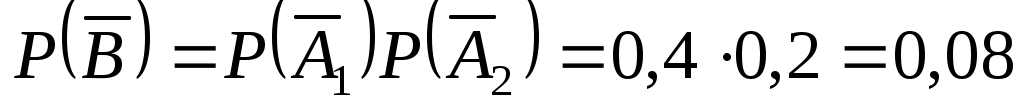
, то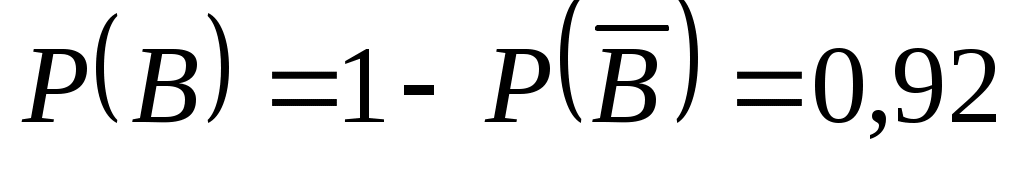 .
.
Формула полной вероятности. Формула Байеса. Вероятность события А, котороеможет произойти при наступлении одного из несовместных событий (гипотез)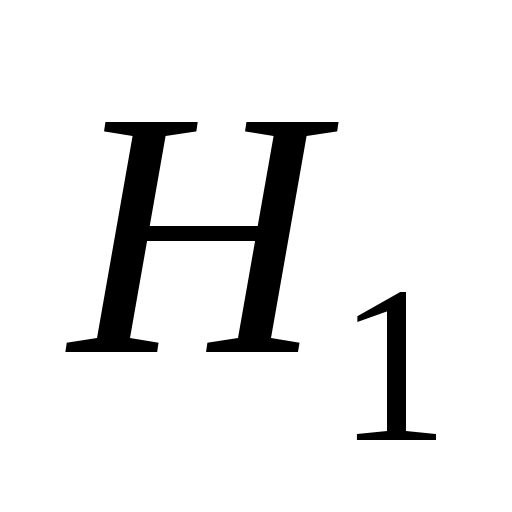 ,
,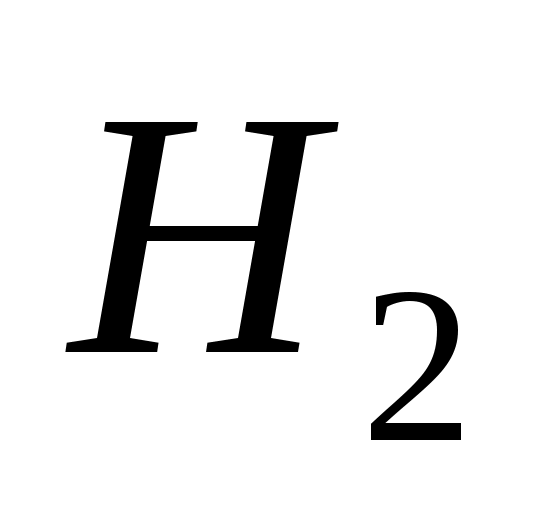 ,…,
,…,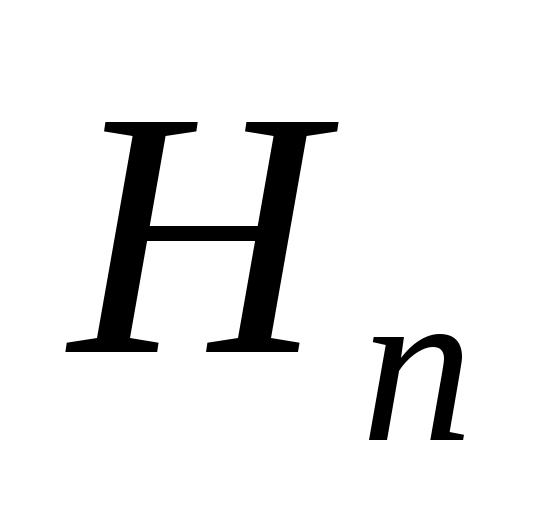 , образующих полную группу событий
, образующих полную группу событий 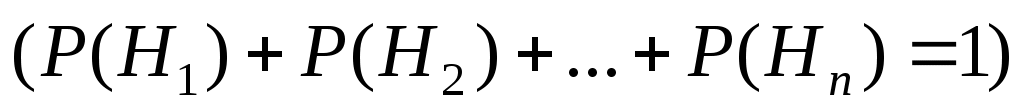 ,вычисляется по формуле
,вычисляется по формуле
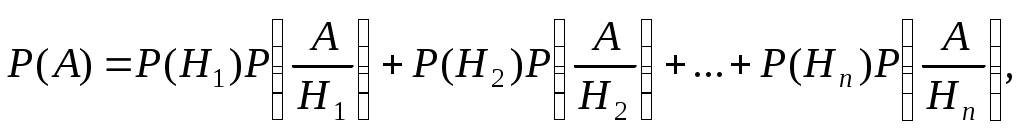
где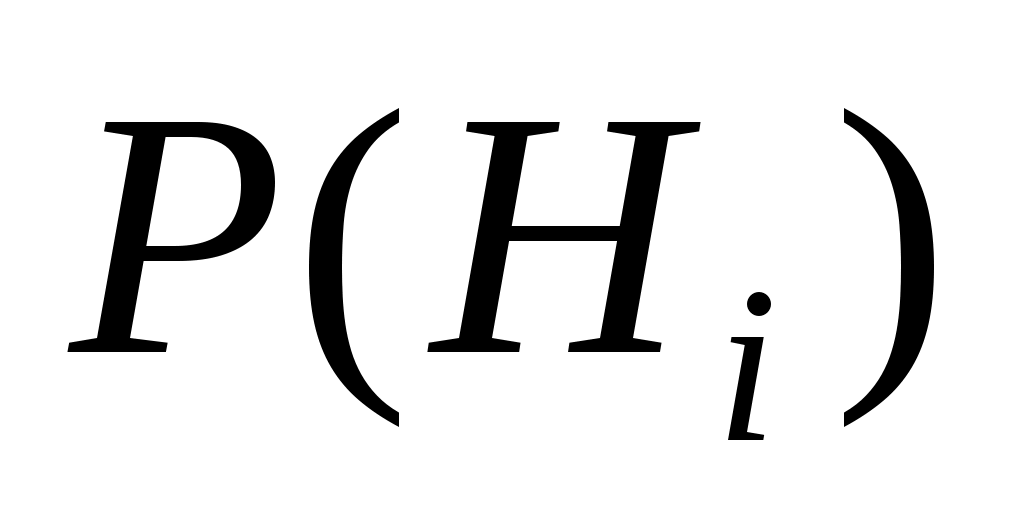 – вероятность события
– вероятность события 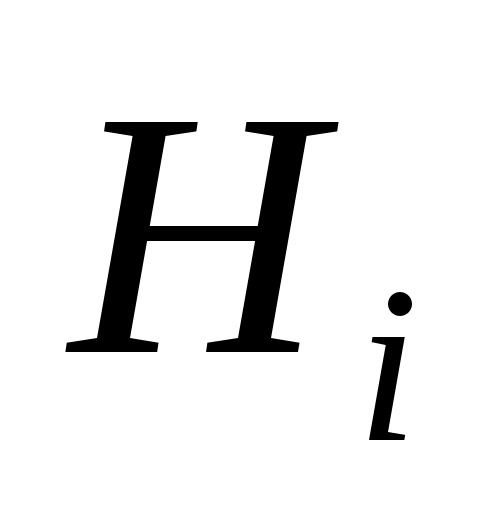 ;
; 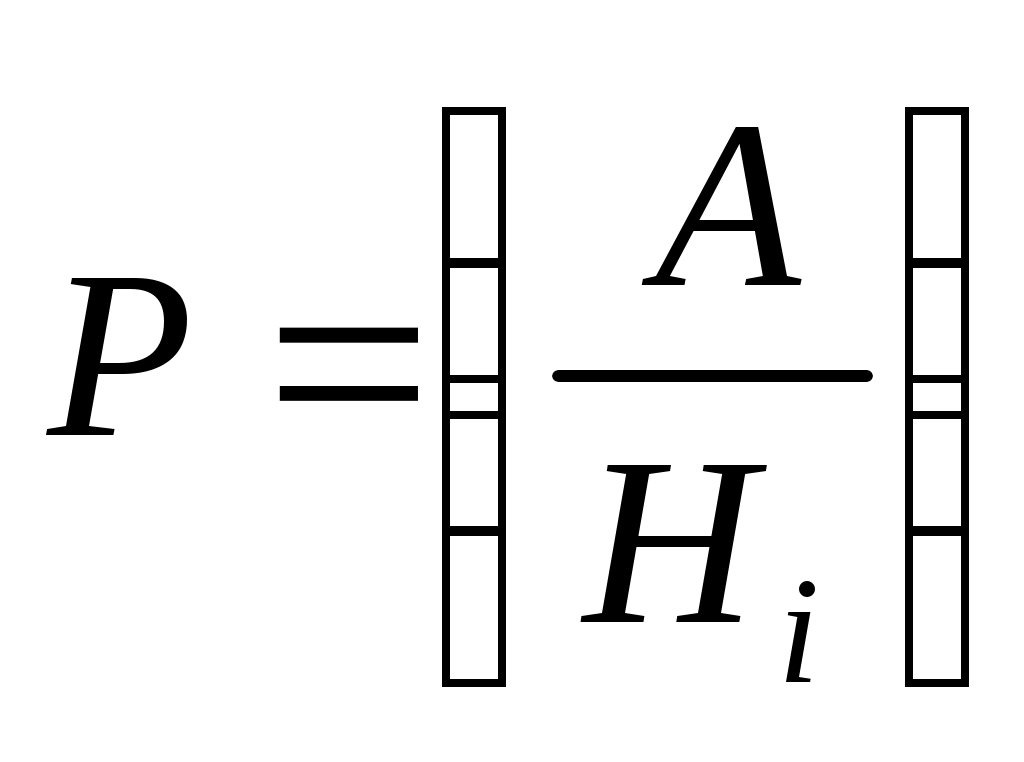 – условная вероятность события A при наступлении события
– условная вероятность события A при наступлении события 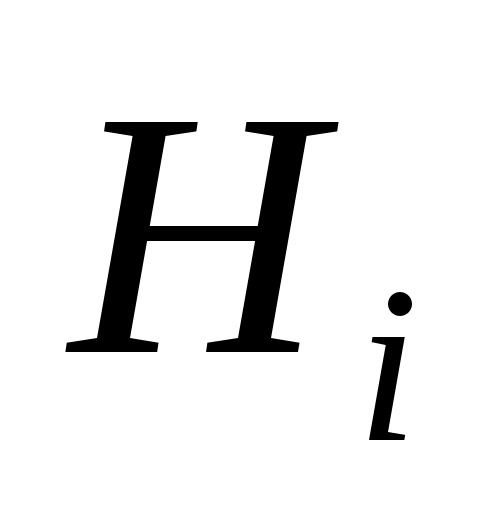 ,
, 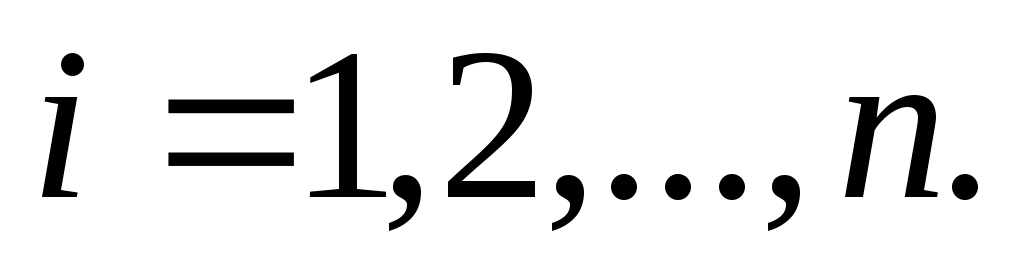
Полученная формула для
 называется формулой полной вероятности и применяется при наличии полной группы несовместных событий.
называется формулой полной вероятности и применяется при наличии полной группы несовместных событий.
С формулой полной вероятности тесно связана формула Байеса. Если до проведения опыта вероятности (априорные) гипотез были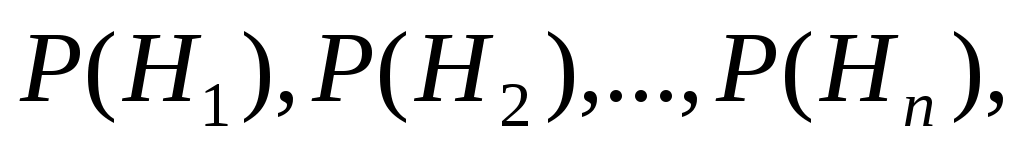 а в результате опыта событие Aпроизошло, то с учетом этого «новые», т.е. условные вероятности (апостериорные) гипотез, вычисляются по формуле
а в результате опыта событие Aпроизошло, то с учетом этого «новые», т.е. условные вероятности (апостериорные) гипотез, вычисляются по формуле
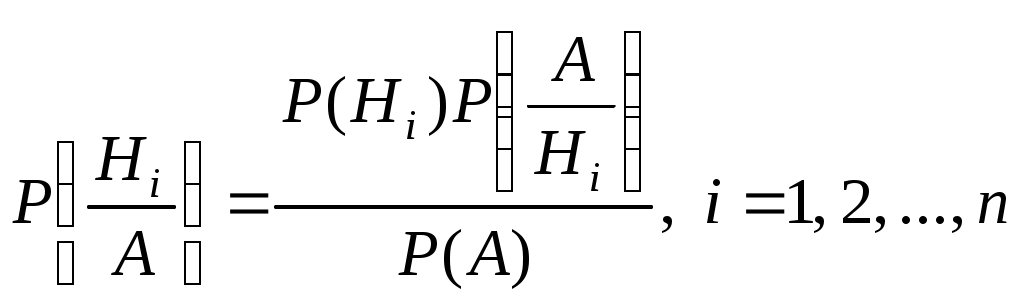 ,
,
где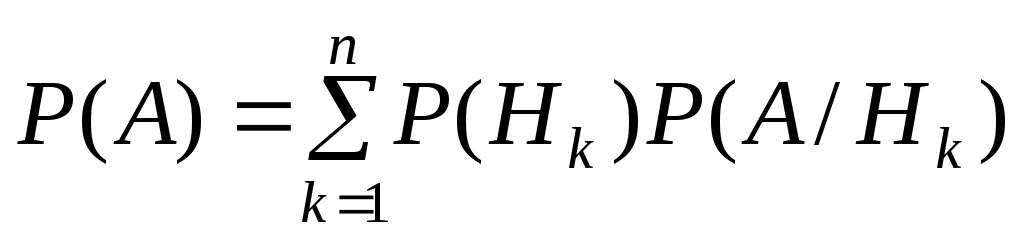 .
.
С помощью формулы Байеса возможно «пересмотреть» вероятность гипотез с учетом полученного (известного) результата опыта.
Пример 5. Имеются два ящика с шарами. В первом ящике шесть белых и четыре черных шара, во втором ящике десять белых и пять черных шаров. Из
первого ящика во второй, не глядя, перекладывается один шар. После этого из второго ящика берут один шар. Найти вероятность того, что этот шар будет белым.
Решение. Пусть событие A – появление белого шара из второго ящика при гипотезах: – из первого ящика во второй переложен белый шар,
– из первого ящика во второй переложен белый шар,  – из первого ящика во второй переложен черный шар. Вероятности гипотез
– из первого ящика во второй переложен черный шар. Вероятности гипотез  и
и  равны вероятности извлечения из первого ящика одного белого или одного черного шара соответственно:
равны вероятности извлечения из первого ящика одного белого или одного черного шара соответственно:
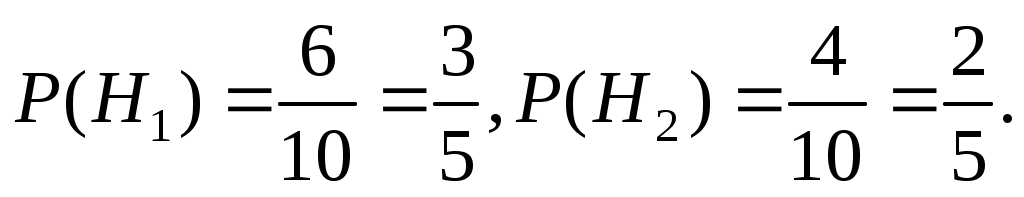
После того, как во второй ящик из первого переложен один шар, количество шаров во втором ящике увеличится на единицу и станет равным 16. При перекладывании белого шара из первого ящика число белых шаров во втором ящике станет равным 11, а при перекладывании черного шара число белых шаров во втором ящике останется прежним. Тогда условные вероятности извлечения белого шара после перекладывания из второго ящика следующие: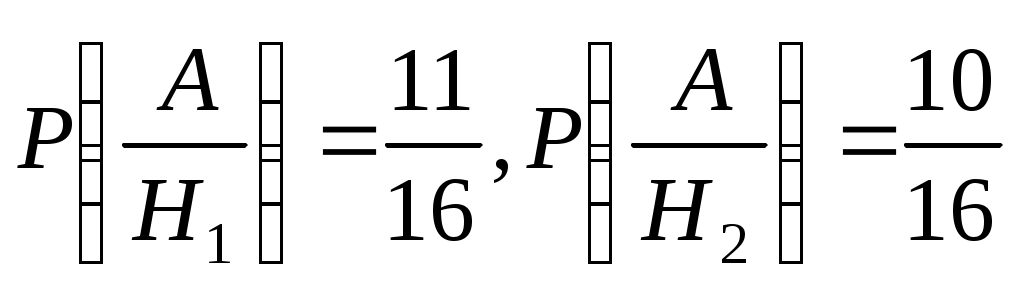 .
.
Искомая вероятность:
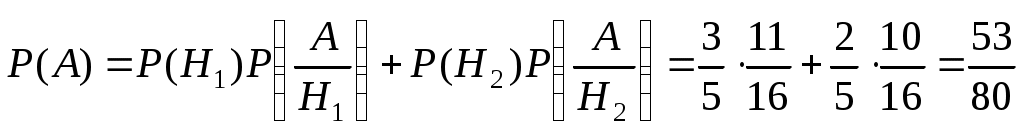 .
.
Пример 6.На трех станках производятся одинаковые детали, причем на первом станке производят 25 %, на втором 35 %, на третьем 40 % всех деталей. В продукции трех станков брак составляет 5, 4 и 2 % соответственно. Все детали поступают на склад.
Найти вероятность того, что случайно выбранная деталь окажется бракованной.
Случайно взятая на складе деталь оказалась бракованной. Какова вероятность, что она изготовлена на первом станке
Решение. Пусть событие A – выбор бракованной детали. Есть три гипотезы: – деталь изготовлена на первом станке;
– деталь изготовлена на первом станке; 
Пример 1. Игральную кость бросают один раз. Найти вероятность появления четного числа очков.
Решение. При подбрасывании одной игральной кости пространство элементарных событий (число выпавших очков) состоит из шести исходов: Ω = {1, 2, 3, 4, 5, 6}. Пусть A – событие, состоящее в появлении четного числа очков. В этом случае событию А благоприятствуют исходы выпадения 2, 4, 6 очков, т.е.
Пример 2. В ящике пять белых и четыре черных шара. Из ящика вынимают три шара. Какова вероятность того, что эти шары белые? Какова вероятность того, что один шар белый?
Решение. Пусть событие A состоит в извлечении трех белых шаров. Общее число исходов
Тогда
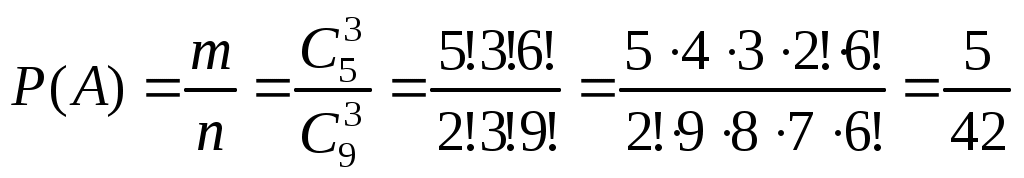 .
.Пусть событие B состоит в извлечении трех шаров, один из которых – белый. Этот шар можно вынуть
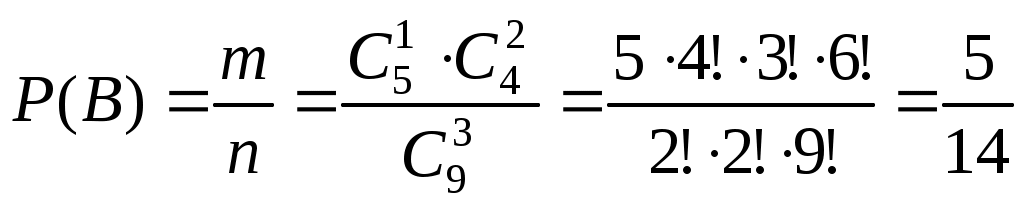 .
.Суммой A+ B двух случайных событий A и B называется событие, состоящее в появлении события A или события B,или обоих этих событий.
Произведением AB двух событий A и B называется событие, состоящее в совместном появлении события Aи события B.
Противоположным по отношению к событию A называется событие
Вероятность суммы совместных событий
Если события A и B несовместны, то
Так как противоположные события несовместны и образуют полную группу, то сумма их вероятностей
Условное событие
Вероятность произведения событий
где
Если события Aи B независимы,
Пример 3. Разрыв электрической цепи происходит при выходе из строя двух элементов
A и B или двух элементов C и D. Найти вероятность разрыва цепи, если элементы выходят из строя независимо друг от друга с вероятностями 0,3 и 0,6, 0,4 и 0,5 соответственно.
Решение. Если события A, B, C, D – выход из строя соответствующих элементов, то по определению произведения и суммы событий согласно условию задачи разрыв цепи есть событие
События A, B, C, Dнезависимы, но могут быть совместными, и следовательно,
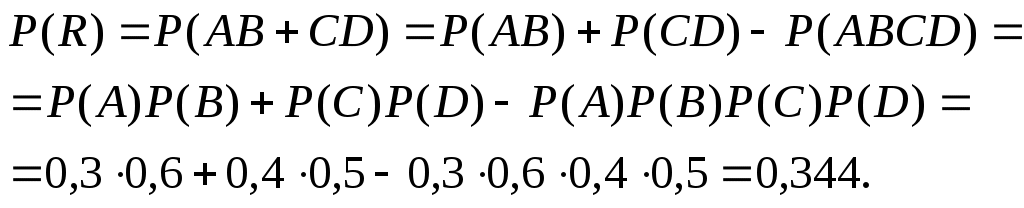
Решение. Если
Пусть событие
, то
Формула полной вероятности. Формула Байеса. Вероятность события А, котороеможет произойти при наступлении одного из несовместных событий (гипотез)
где
Полученная формула для
С формулой полной вероятности тесно связана формула Байеса. Если до проведения опыта вероятности (априорные) гипотез были
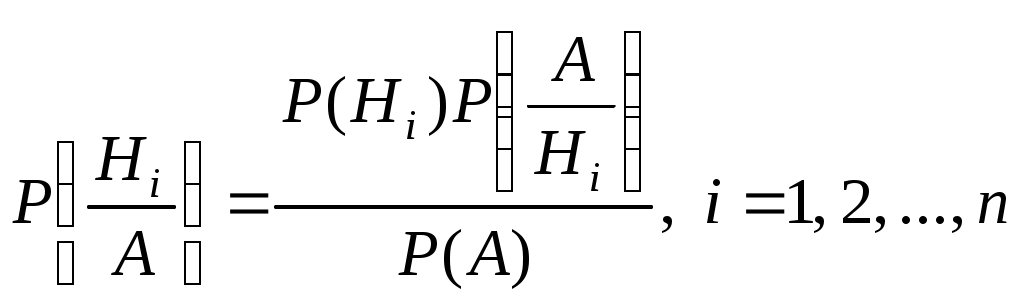 ,
,где
С помощью формулы Байеса возможно «пересмотреть» вероятность гипотез с учетом полученного (известного) результата опыта.
Пример 5. Имеются два ящика с шарами. В первом ящике шесть белых и четыре черных шара, во втором ящике десять белых и пять черных шаров. Из
первого ящика во второй, не глядя, перекладывается один шар. После этого из второго ящика берут один шар. Найти вероятность того, что этот шар будет белым.
Решение. Пусть событие A – появление белого шара из второго ящика при гипотезах:
После того, как во второй ящик из первого переложен один шар, количество шаров во втором ящике увеличится на единицу и станет равным 16. При перекладывании белого шара из первого ящика число белых шаров во втором ящике станет равным 11, а при перекладывании черного шара число белых шаров во втором ящике останется прежним. Тогда условные вероятности извлечения белого шара после перекладывания из второго ящика следующие:
Искомая вероятность:
Пример 6.На трех станках производятся одинаковые детали, причем на первом станке производят 25 %, на втором 35 %, на третьем 40 % всех деталей. В продукции трех станков брак составляет 5, 4 и 2 % соответственно. Все детали поступают на склад.
Найти вероятность того, что случайно выбранная деталь окажется бракованной.
Случайно взятая на складе деталь оказалась бракованной. Какова вероятность, что она изготовлена на первом станке
Решение. Пусть событие A – выбор бракованной детали. Есть три гипотезы: