ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 177
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
– деталь изготовлена на втором станке; 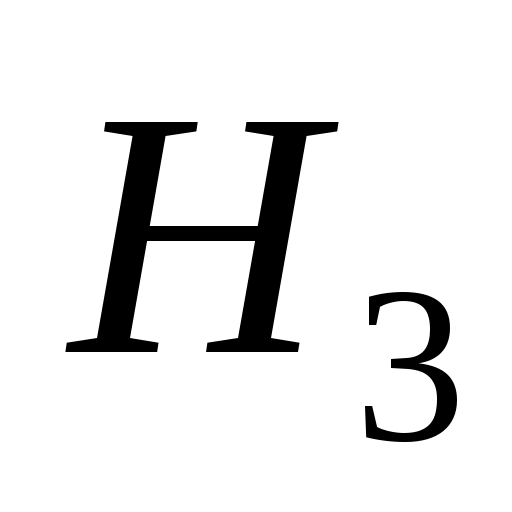 – деталь изготовлена на третьем станке.
– деталь изготовлена на третьем станке.
По условию вероятности этих гипотез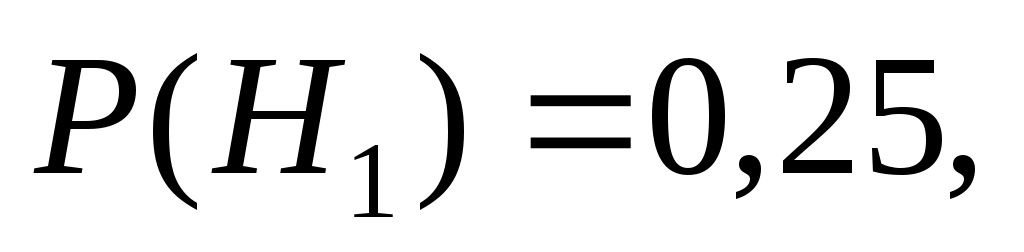
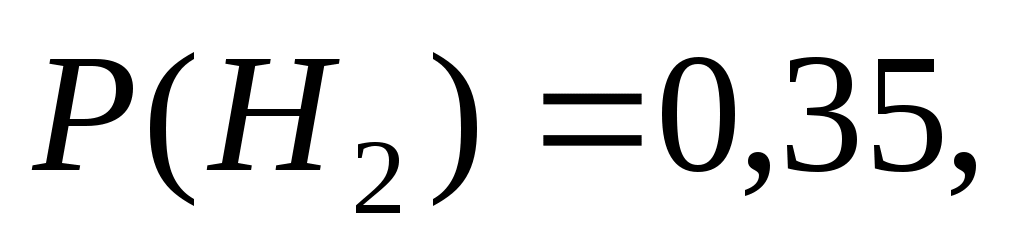
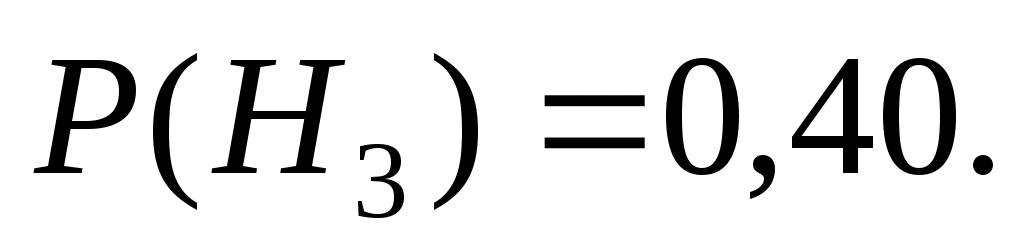 Условные вероятности события A – вероятности появления бракованной детали в продукции первого, второго или третьего станков:
Условные вероятности события A – вероятности появления бракованной детали в продукции первого, второго или третьего станков: 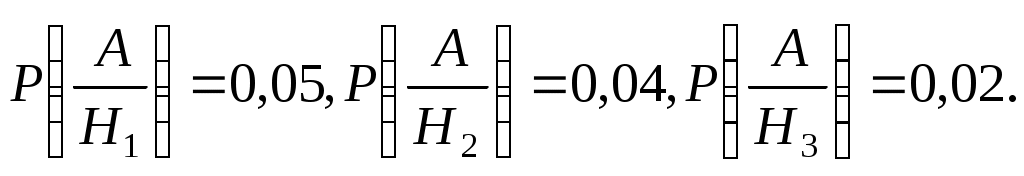
Тогда:
а) вероятность события A находим по формуле полной вероятности:
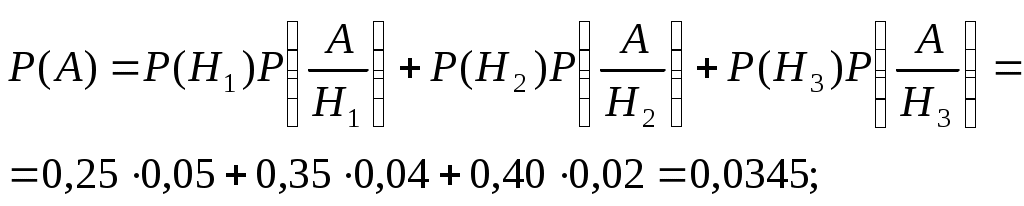
б) вероятность изготовления на первом станке находим по формуле Байеса:
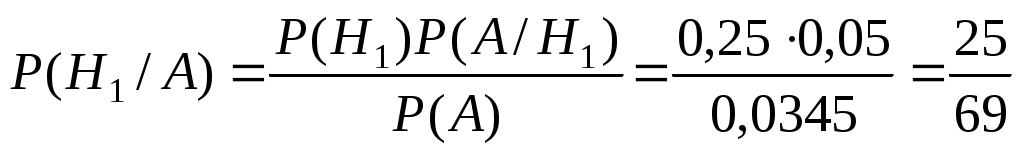 .
.
Испытания называются независимыми, если результаты любого испытания не зависят от результатов других испытаний.
Формула Бернулли. Пусть производится n независимых испытаний в одинаковых условиях и каждое испытание имеет только два исхода: событие A (успех) или событие Ā (неуспех). Вероятность появления события A (успех) при одном испытании обозначим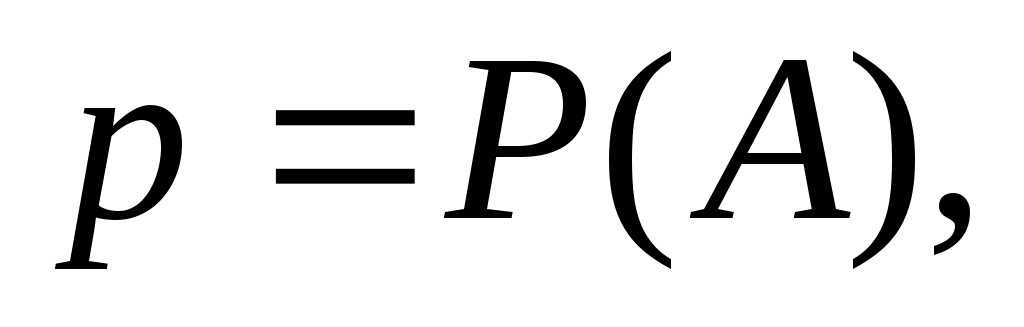 а вероятность неуспеха обозначим
а вероятность неуспеха обозначим 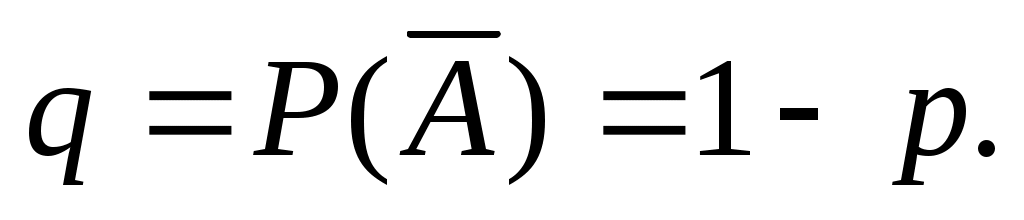 Вероятность
Вероятность 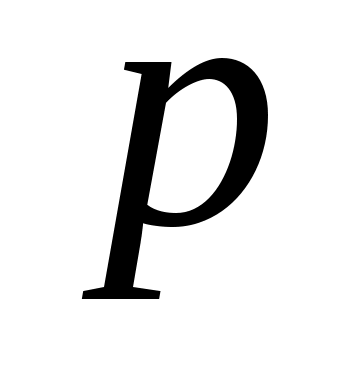 постоянна во всех испытаниях и отлична от нуля и единицы. Вероятность того, что при
постоянна во всех испытаниях и отлична от нуля и единицы. Вероятность того, что при 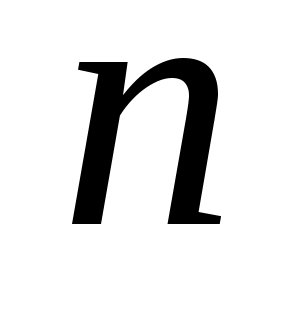 повторных испытаниях успех произойдет ровно
повторных испытаниях успех произойдет ровно 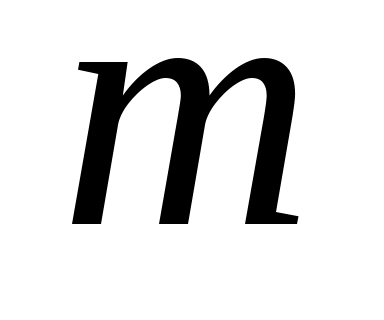 раз, определяется по формуле Бернулли:
раз, определяется по формуле Бернулли:
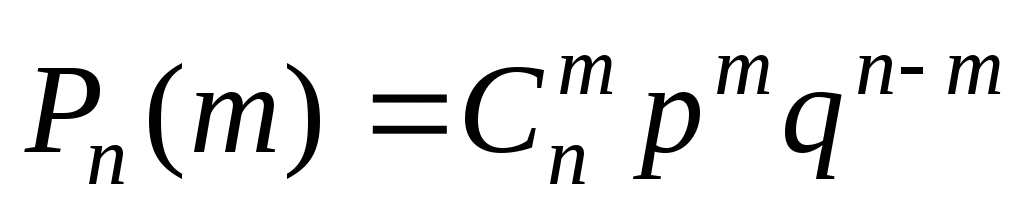 .
.
Вероятность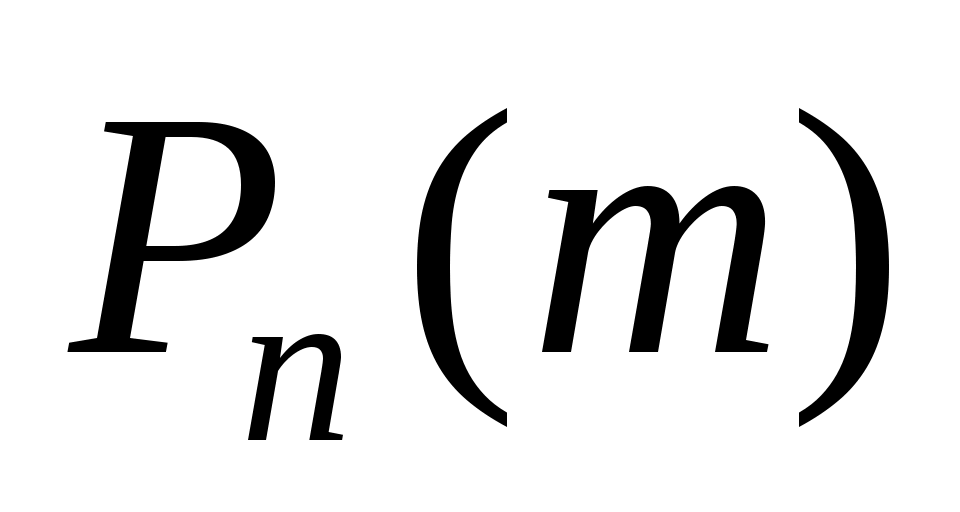 сначала увеличивается при изменении m от нуля до некоторого значения
сначала увеличивается при изменении m от нуля до некоторого значения 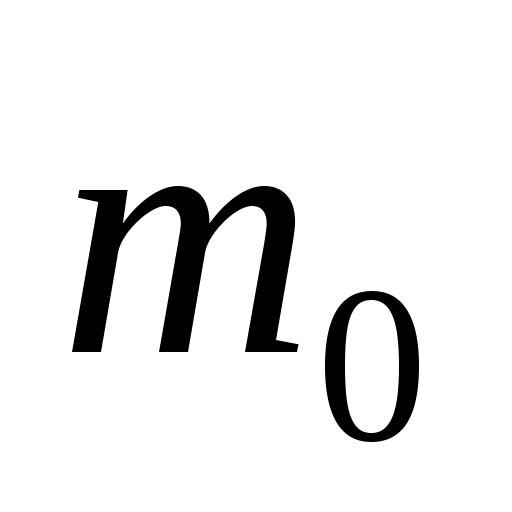 , а затем уменьшается при изменении
, а затем уменьшается при изменении 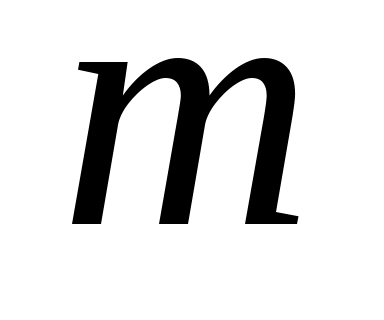 от
от 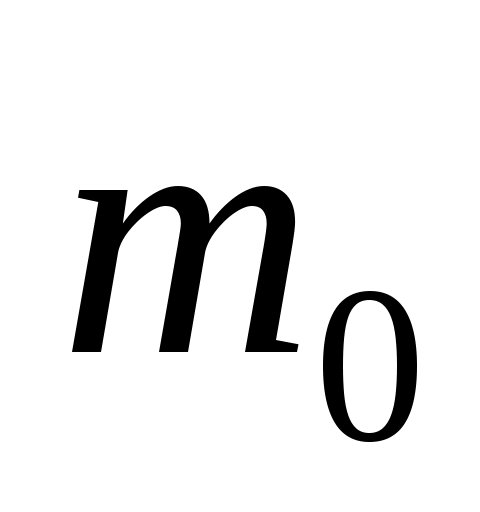 до
до 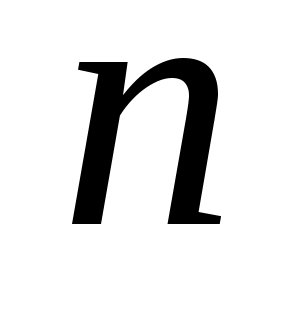 . Величина
. Величина 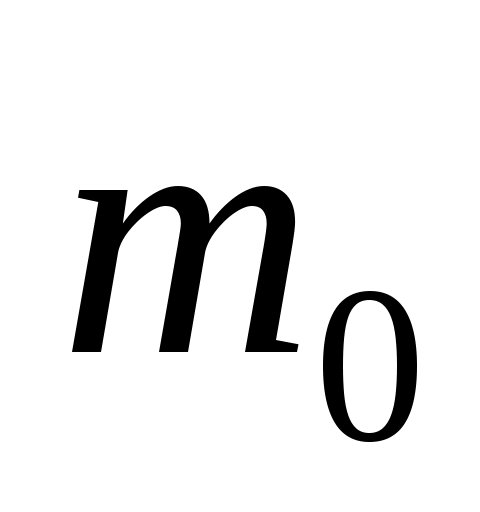 называется наивероятнейшим числом наступления события A в
называется наивероятнейшим числом наступления события A в 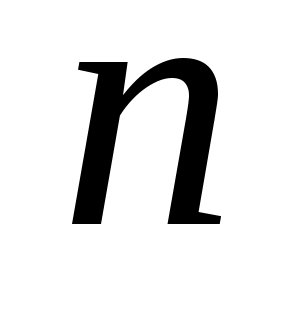 испытаниях и удовлетворяет условию:
испытаниях и удовлетворяет условию: 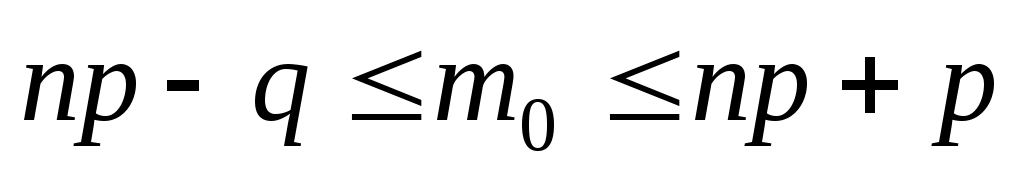 . При целом значении
. При целом значении 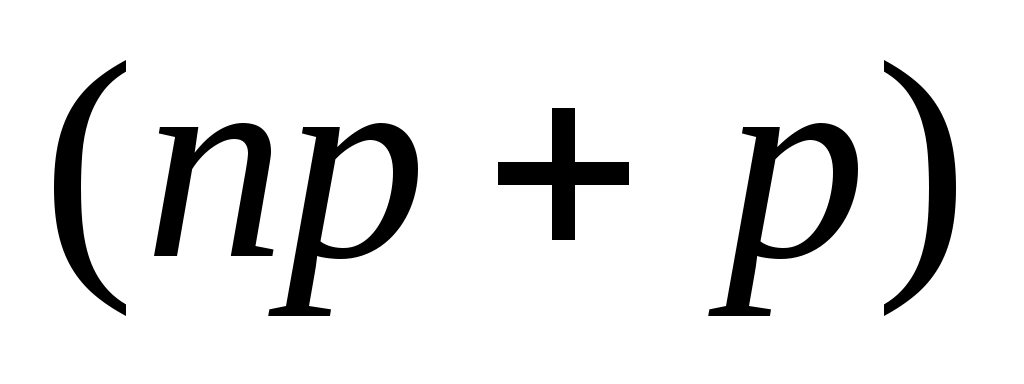
имеются два значения: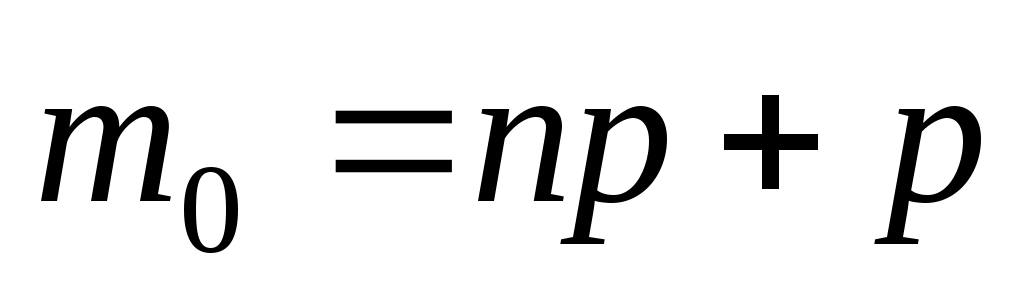 и
и 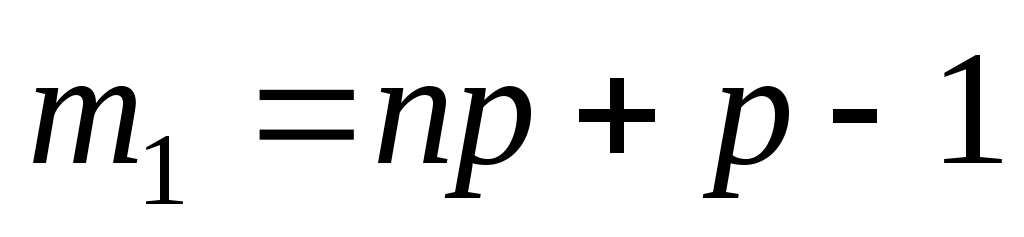 ; принецелом значении одно –
; принецелом значении одно –  .
.
Вероятность хотя бы одного успеха в nнезависимых испытаниях, произведенных в одинаковых условиях,
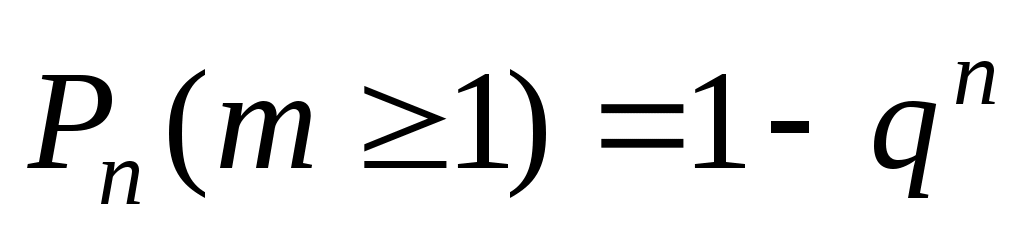 .
.
Для приближенного вычисления вероятностей применяют предельные теоремы Муавра – Лапласа и Пуассона.
применяют предельные теоремы Муавра – Лапласа и Пуассона.
Локальная теорема Муавра – Лапласа. Если число независимых испытаний, производимых в одинаковых условиях, достаточно велико, и вероятность p появления события Aв каждом испытании постоянна и отлична от нуля и единицы, то вероятность
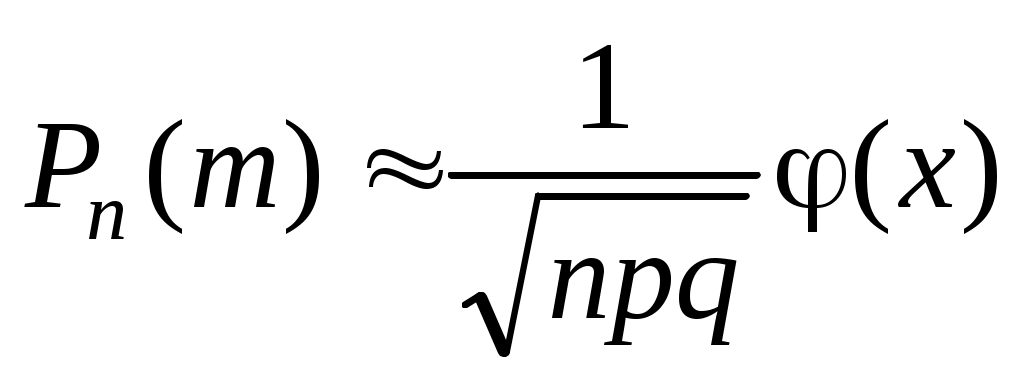 ,
,
где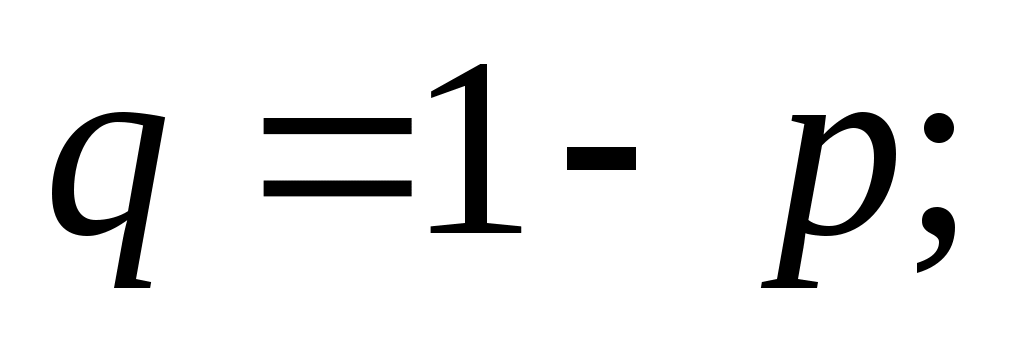
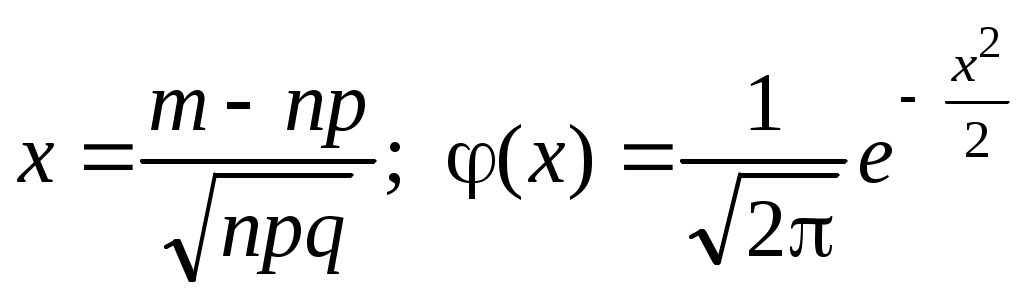 ;
; 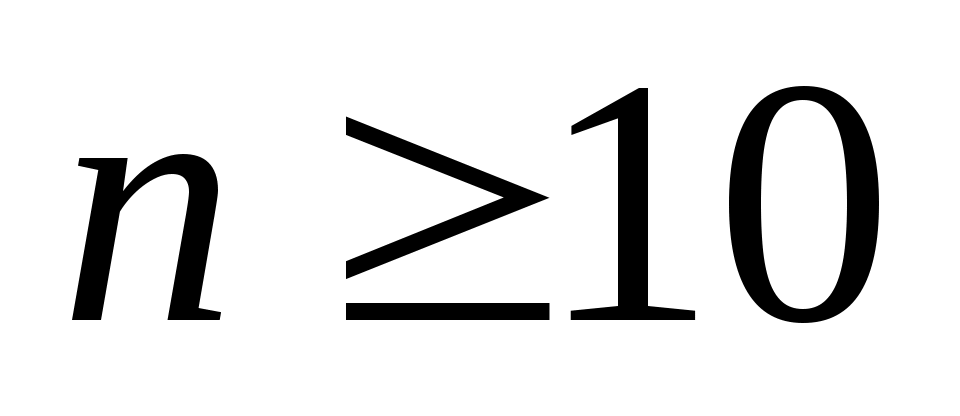 .
.
Отметим, что функция Гаусса (х) – четная и для нее составлены таблицы (прил.1).
Вероятность появления события A в независимых испытаниях не менее
независимых испытаниях не менее 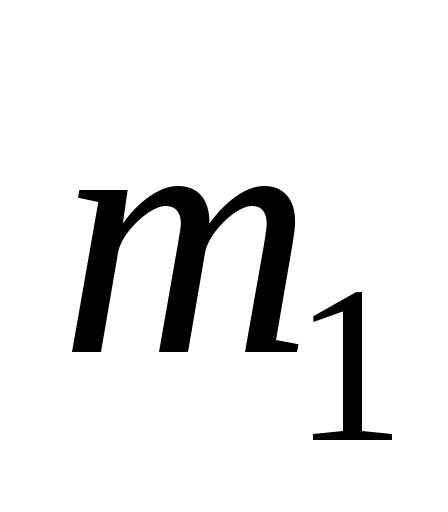 и не более
и не более  раз
раз
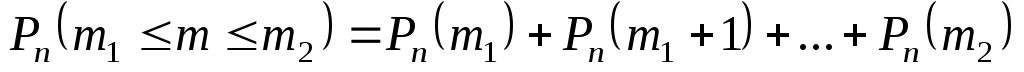 .
.
При большом числе испытаний вероятность
вероятность 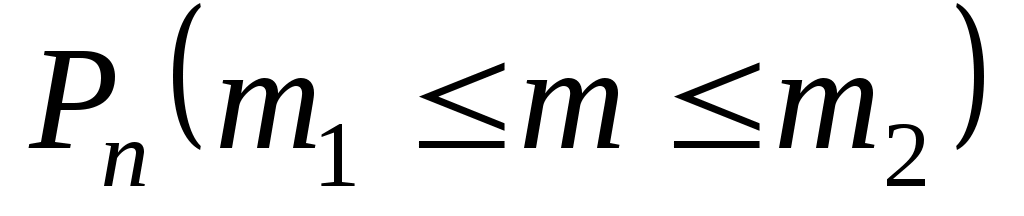 находят с помощью интегральной теоремы Муавра – Лапласа.
находят с помощью интегральной теоремы Муавра – Лапласа.
Интегральная теорема Муавра – Лапласа. Если число испытаний достаточно велико и вероятность
достаточно велико и вероятность  появления события A в каждом испытании постоянна и отлична от нуля и единицы, то вероятность
появления события A в каждом испытании постоянна и отлична от нуля и единицы, то вероятность
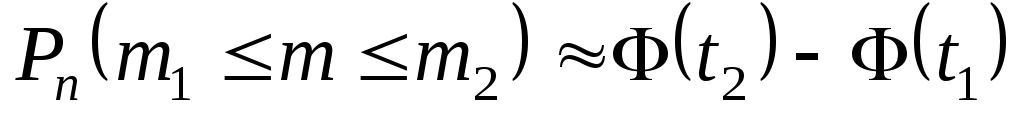 ,
,
где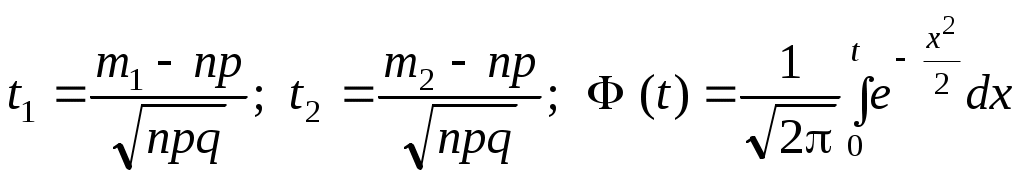 ;
; 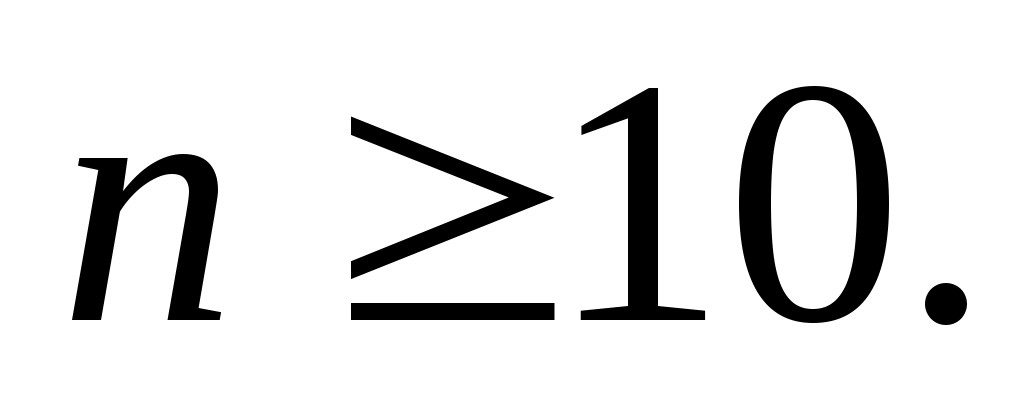
функция Лапласа Ф(t) – нечетная и для нее составлены таблицы (прил.2).
Теорема Бернулли. Если в n независимых испытаниях вероятность появления события A постоянна для каждого испытания и отлична от нуля и единицы, то при достаточно большом числе испытаний с вероятностью как угодно близкой к единице (практически достоверной) относительная частота события A будет сколь угодно мало отличаться от его вероятности.
Например, из интегральной теоремы Муавра – Лапласа следует, что для любого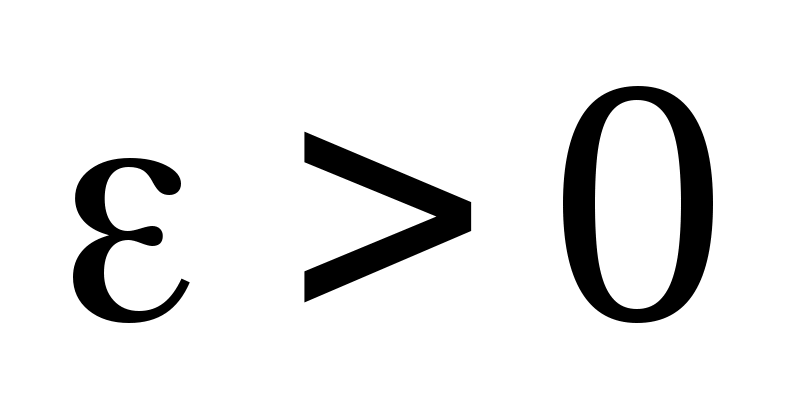 (
(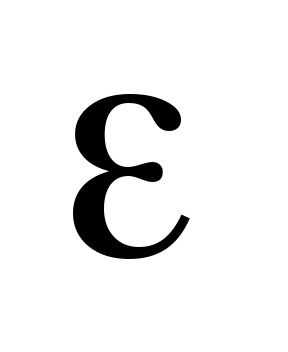 – малое положительное число) имеет место формула
– малое положительное число) имеет место формула
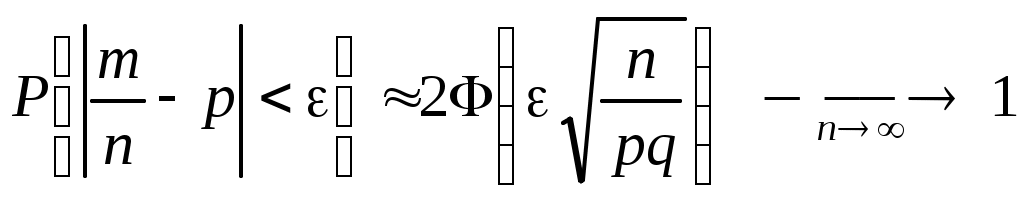 .
.
Закон Пуассона. Пусть число n независимых испытаний велико, вероятность появления события A в каждом испытании постоянна и представляет малое число. Тогда при
появления события A в каждом испытании постоянна и представляет малое число. Тогда при 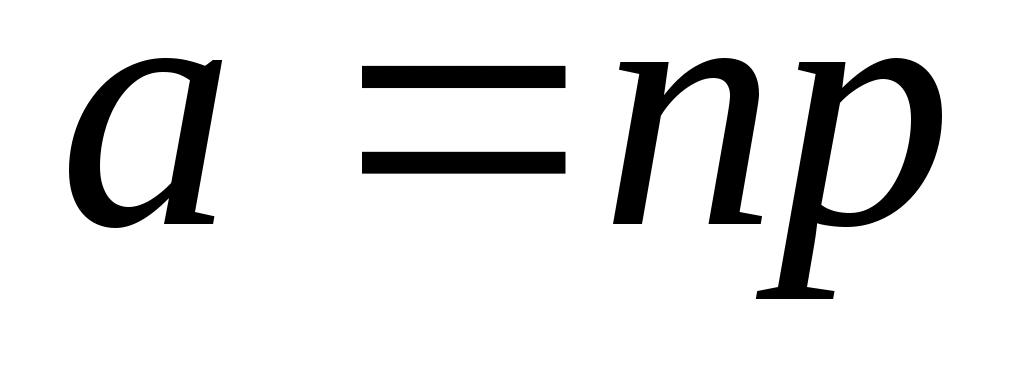 (среднее число появлений события в
(среднее число появлений события в  испытаниях) имеем приближенную формулу вероятности редких событий:
испытаниях) имеем приближенную формулу вероятности редких событий:
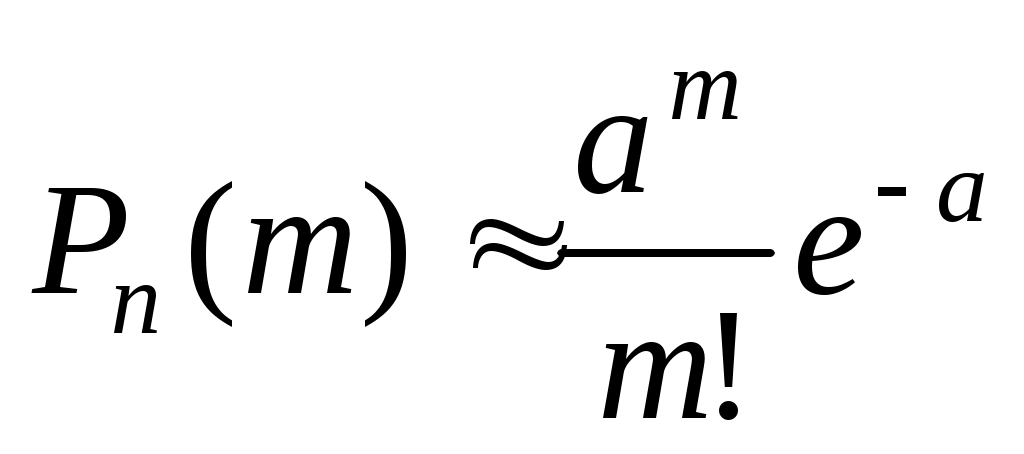 .
.
Такое событие A называют редким событием, а закон распределения Пуассона – законом редких событий.
Пример 7. Производятся четыре независимых выстрела по мишени. Вероятность попадания в мишень при одном выстреле постоянна и равна 0,8. Найти вероятность:
двух попаданий в мишень;
не менее двух попаданий в мишень.
Решение. По условию имеем число выстрелов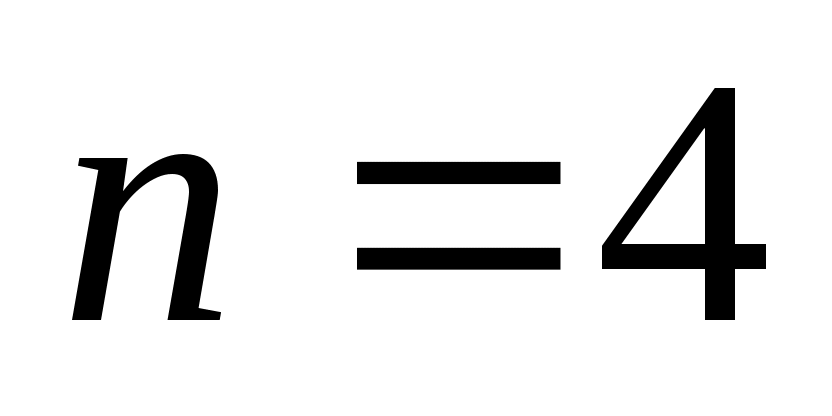 , вероятность попадания в мишень при одном выстреле
, вероятность попадания в мишень при одном выстреле 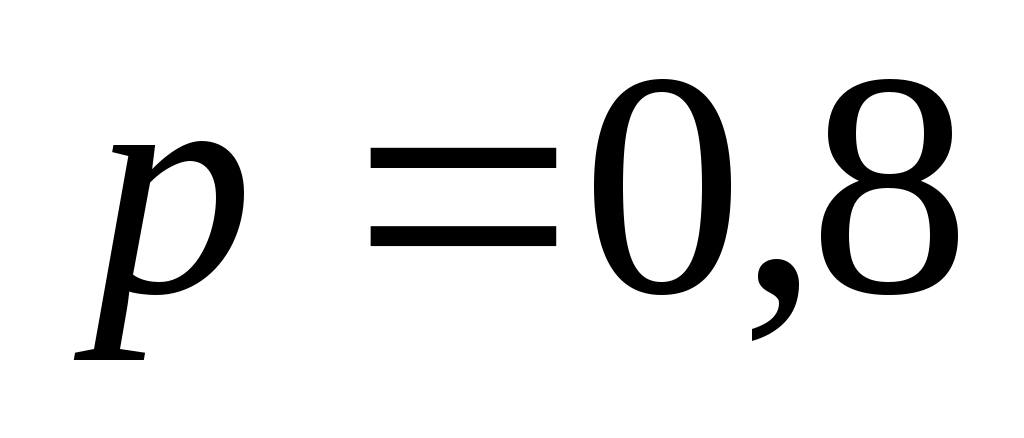 ; тогда вероятность промаха при одном выстреле
; тогда вероятность промаха при одном выстреле 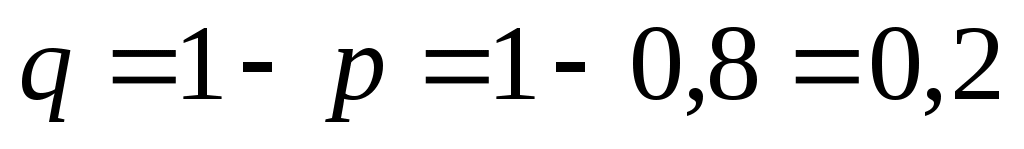 .
.
Вероятность двух попаданий в мишень при четырех выстрелах:
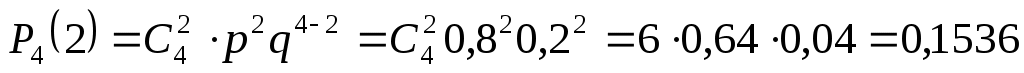 .
.
Не менее двух попаданий в мишень при четырех выстрелах означает два или три, или четыре попадания в мишень. Вероятность не менее двух попаданий в мишень
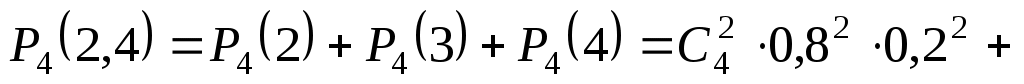
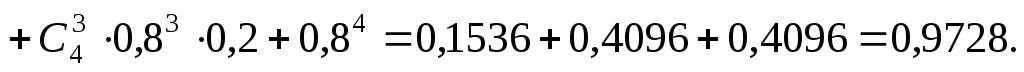
Пример 8. При установившемся технологическом процессе из 100 изготовленных деталей 10 деталей имеют дефект. Найти вероятность того, что среди 80 изготовленных деталей семь будут иметь дефект.
Решение. В этой задаче испытание состоит в проверке каждой детали на наличие дефекта. Пусть событие A – обнаружение дефекта при проверке детали. По условию задачи вероятность события A в каждом опыте постоянна и равна 0,1. Так как число опытов велико, искомую вероятность находят с помощью локальной теоремы Муавра – Лапласа.
Итак,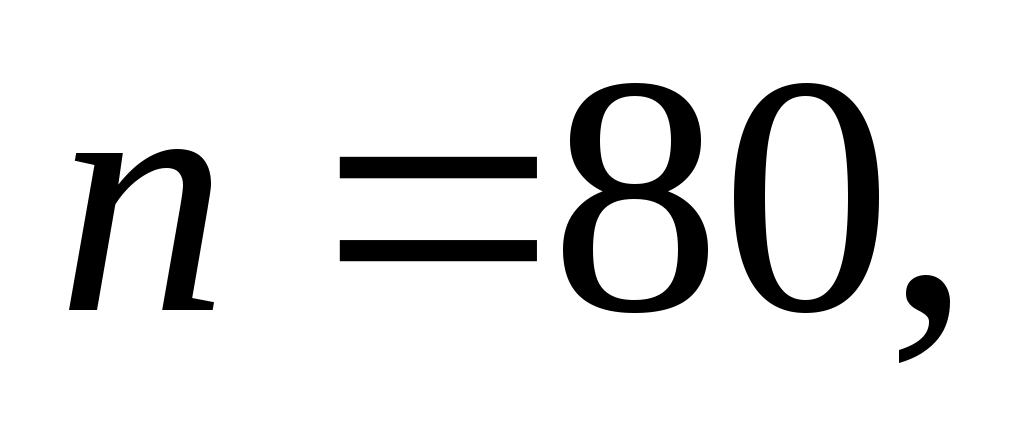
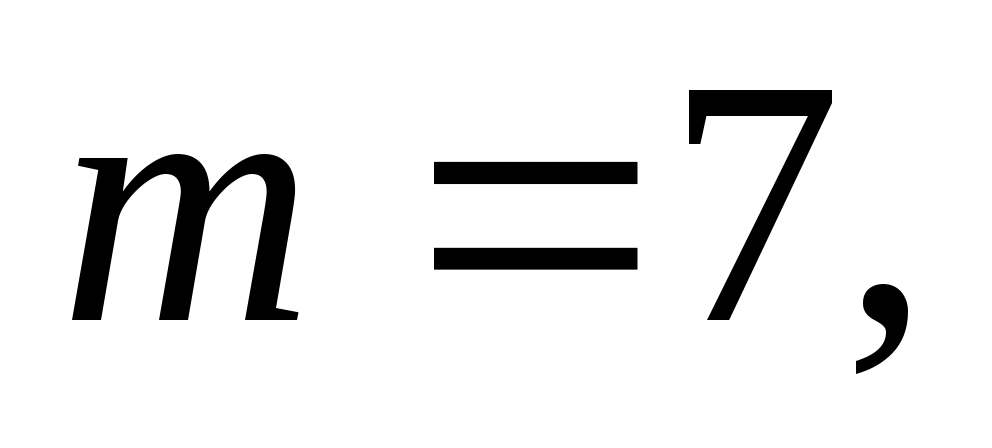
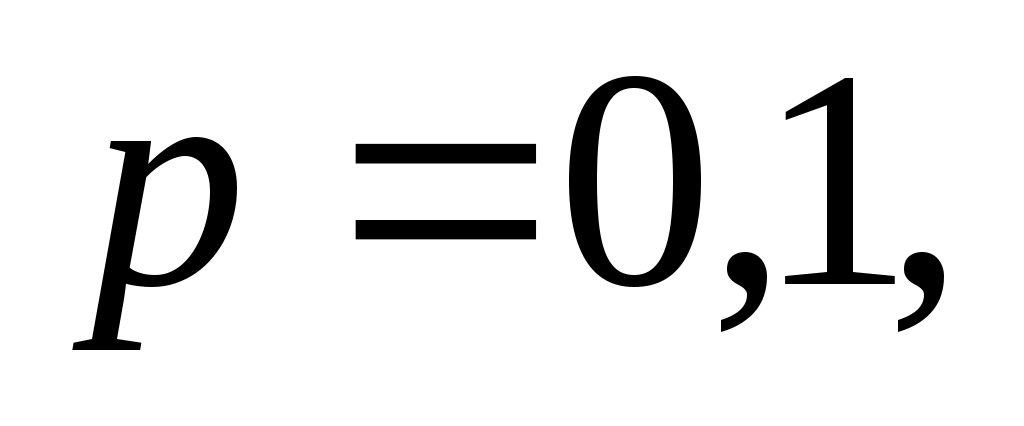
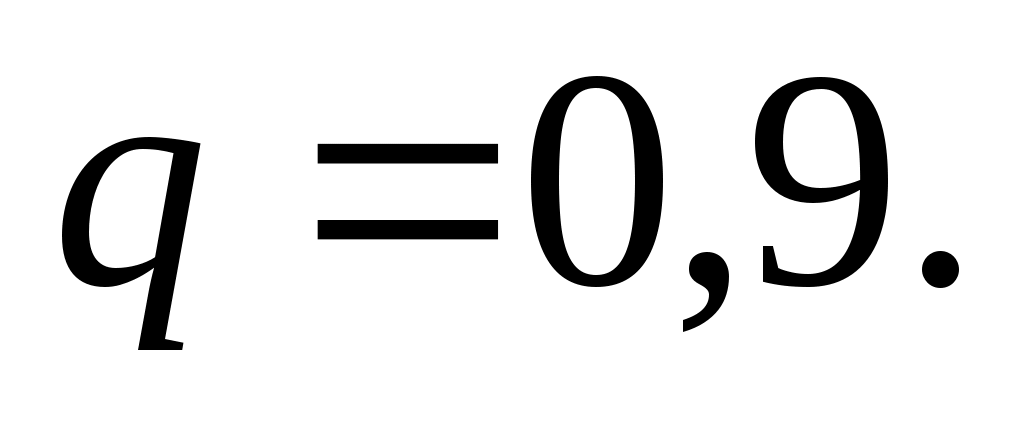
Тогда
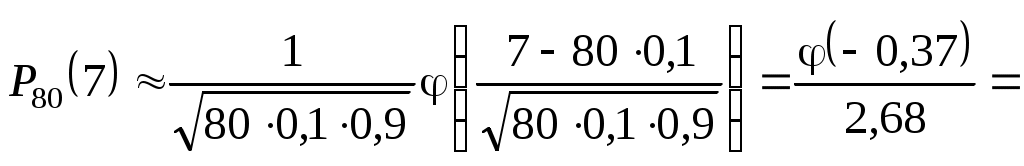
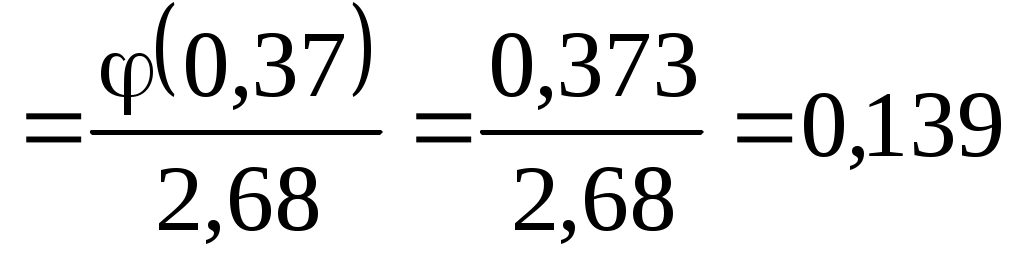
По условию вероятности этих гипотез
Тогда:
а) вероятность события A находим по формуле полной вероятности:
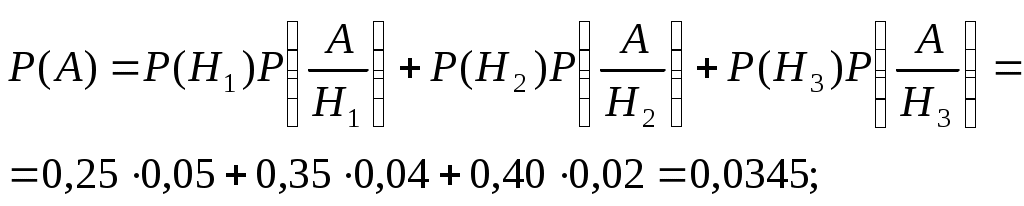
б) вероятность изготовления на первом станке находим по формуле Байеса:
1.2. Повторение независимых опытов
Испытания называются независимыми, если результаты любого испытания не зависят от результатов других испытаний.
Формула Бернулли. Пусть производится n независимых испытаний в одинаковых условиях и каждое испытание имеет только два исхода: событие A (успех) или событие Ā (неуспех). Вероятность появления события A (успех) при одном испытании обозначим
Вероятность
имеются два значения:
Вероятность хотя бы одного успеха в nнезависимых испытаниях, произведенных в одинаковых условиях,
Для приближенного вычисления вероятностей
Локальная теорема Муавра – Лапласа. Если число независимых испытаний, производимых в одинаковых условиях, достаточно велико, и вероятность p появления события Aв каждом испытании постоянна и отлична от нуля и единицы, то вероятность
где
Отметим, что функция Гаусса (х) – четная и для нее составлены таблицы (прил.1).
Вероятность появления события A в
При большом числе испытаний
Интегральная теорема Муавра – Лапласа. Если число испытаний
где
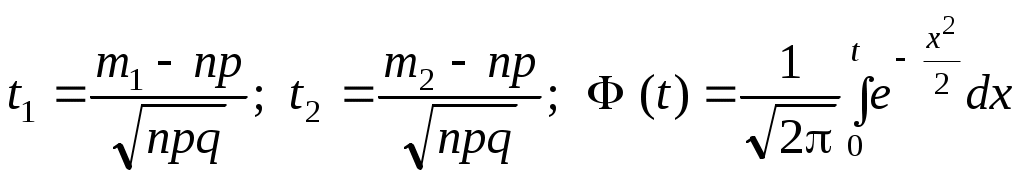 ;
; функция Лапласа Ф(t) – нечетная и для нее составлены таблицы (прил.2).
Теорема Бернулли. Если в n независимых испытаниях вероятность появления события A постоянна для каждого испытания и отлична от нуля и единицы, то при достаточно большом числе испытаний с вероятностью как угодно близкой к единице (практически достоверной) относительная частота события A будет сколь угодно мало отличаться от его вероятности.
Например, из интегральной теоремы Муавра – Лапласа следует, что для любого
Закон Пуассона. Пусть число n независимых испытаний велико, вероятность
Такое событие A называют редким событием, а закон распределения Пуассона – законом редких событий.
Пример 7. Производятся четыре независимых выстрела по мишени. Вероятность попадания в мишень при одном выстреле постоянна и равна 0,8. Найти вероятность:
двух попаданий в мишень;
не менее двух попаданий в мишень.
Решение. По условию имеем число выстрелов
Вероятность двух попаданий в мишень при четырех выстрелах:
Не менее двух попаданий в мишень при четырех выстрелах означает два или три, или четыре попадания в мишень. Вероятность не менее двух попаданий в мишень
Пример 8. При установившемся технологическом процессе из 100 изготовленных деталей 10 деталей имеют дефект. Найти вероятность того, что среди 80 изготовленных деталей семь будут иметь дефект.
Решение. В этой задаче испытание состоит в проверке каждой детали на наличие дефекта. Пусть событие A – обнаружение дефекта при проверке детали. По условию задачи вероятность события A в каждом опыте постоянна и равна 0,1. Так как число опытов велико, искомую вероятность находят с помощью локальной теоремы Муавра – Лапласа.
Итак,
Тогда