ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 179
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, находят критическое значение 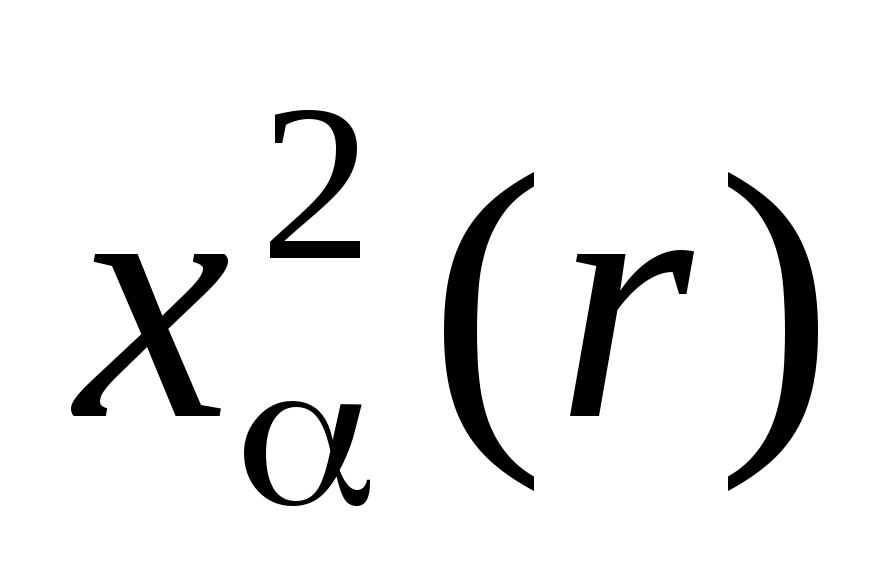 . Вычисленное по выборке значение
. Вычисленное по выборке значение 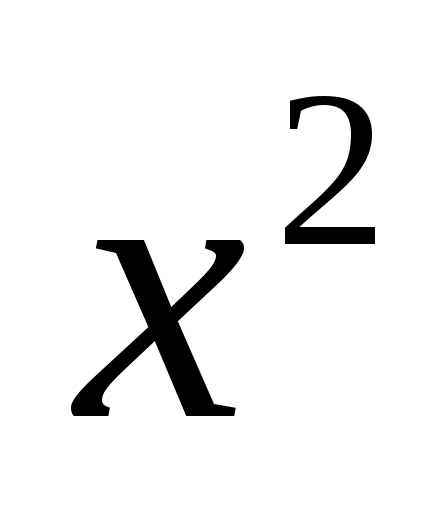 сравнивают с критическим значением: если
сравнивают с критическим значением: если 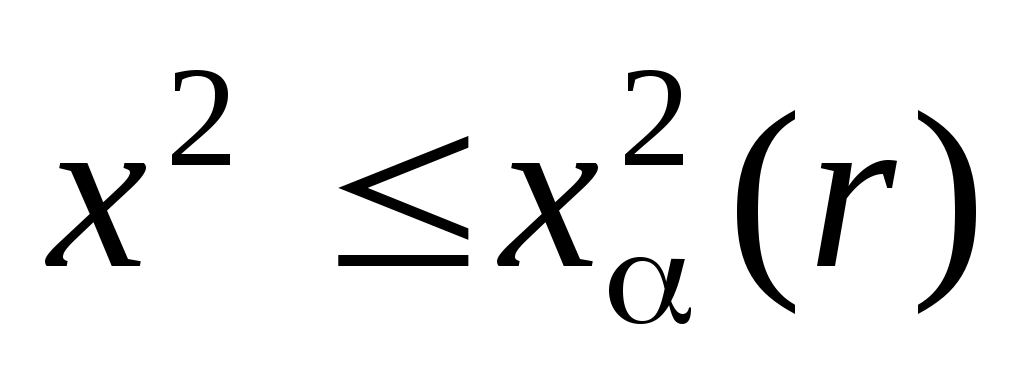 , то различие эмпирических данных с теоретическим распределением можно считать несущественным и гипотеза о согласии эмпирических данных с теоретическим распределением не отвергается; если
, то различие эмпирических данных с теоретическим распределением можно считать несущественным и гипотеза о согласии эмпирических данных с теоретическим распределением не отвергается; если 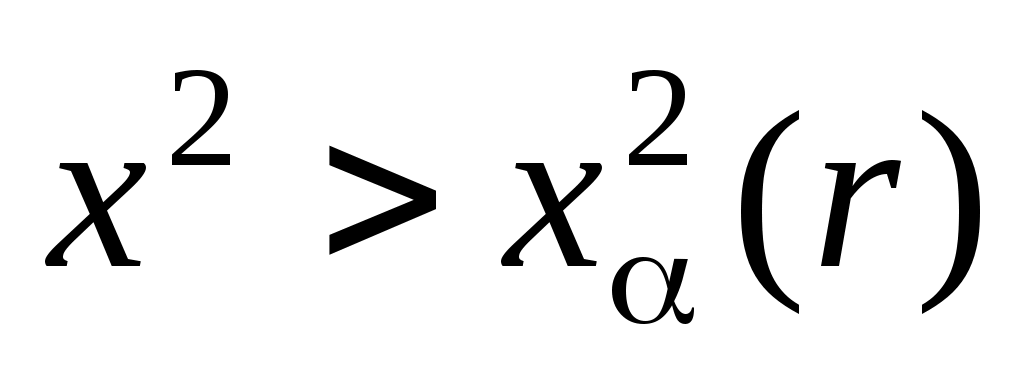 , называемой критической областью, то различия существенны и гипотезу о согласии следует отвергнуть.
, называемой критической областью, то различия существенны и гипотезу о согласии следует отвергнуть.
Отметим, что при использовании критерия Пирсона значения, частоты которых малы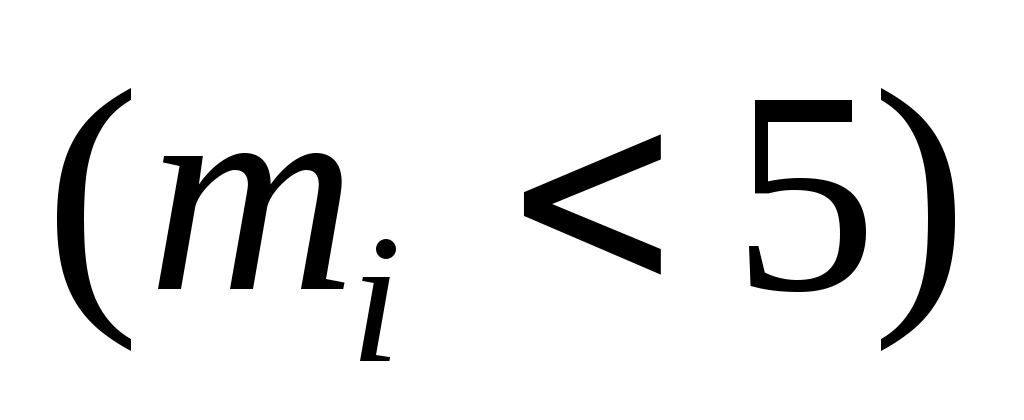 можно объединить (обычно это крайние значения или интервалы).
можно объединить (обычно это крайние значения или интервалы).
Пример 15. При проведении испытаний материала на разрыв получено 50 значений, характеризующих прочность на разрыв. По этим данным составлен сгруппированный вариационный ряд (масштаб 104 Па).
Оценить согласие полученных данных с нормальным распределением при уровне значимости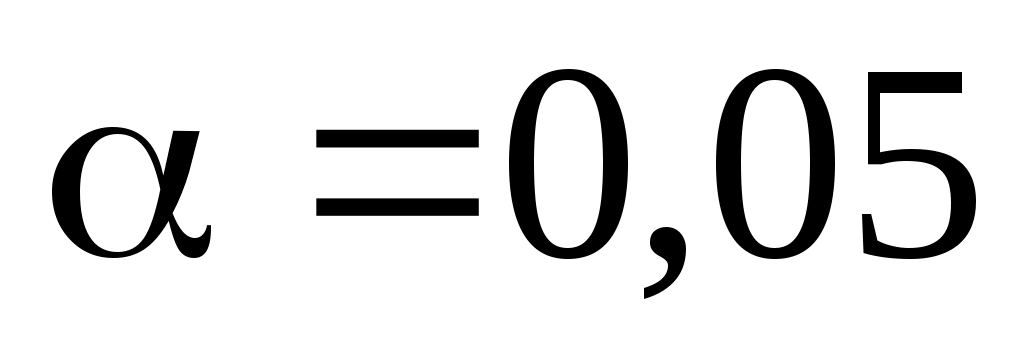 и получить приближенную интервальную оценку для параметра
и получить приближенную интервальную оценку для параметра 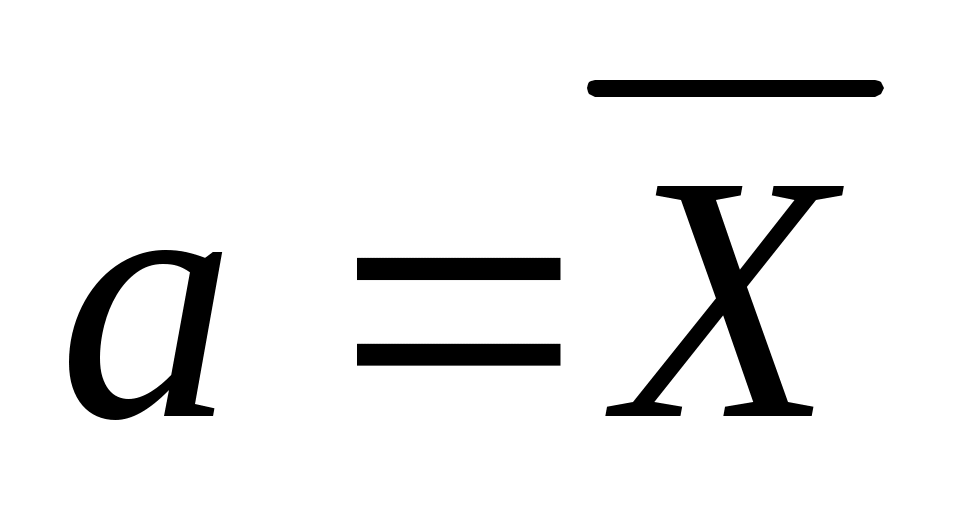 с надежностью
с надежностью 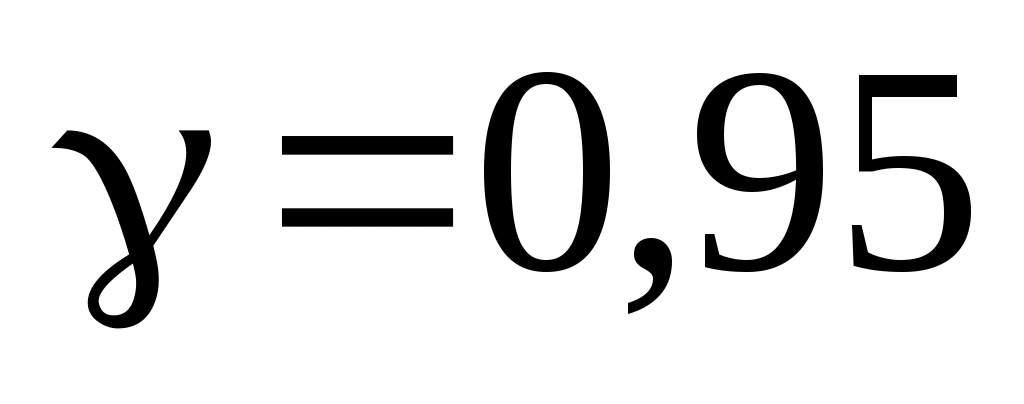 .
.
Решение. Введем условную варианту, определив шаг h = 20 и выбрав ложный нуль C = 190, и найдем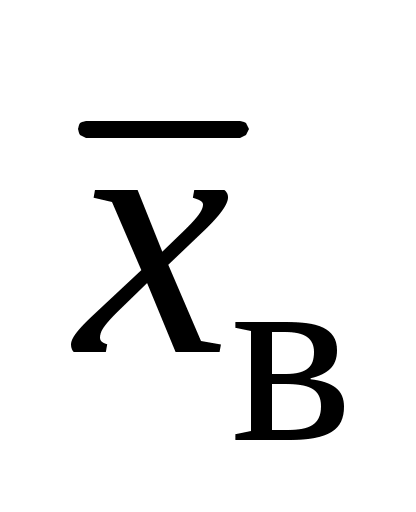 и
и 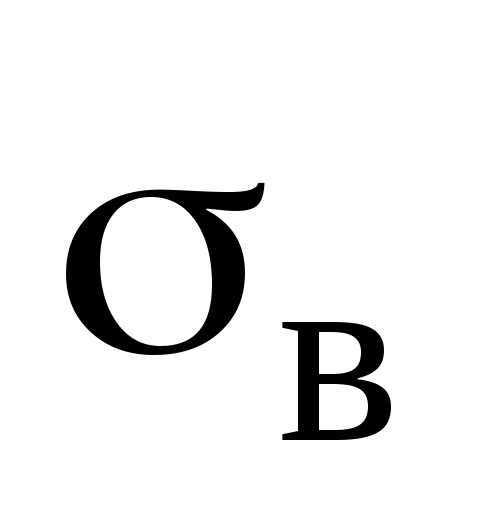 (табл.2).
(табл.2).
Таблица 2
По данным табл.2 имеем n = 50 и
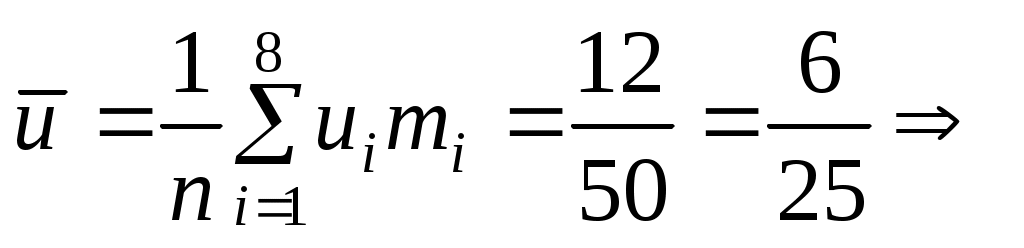
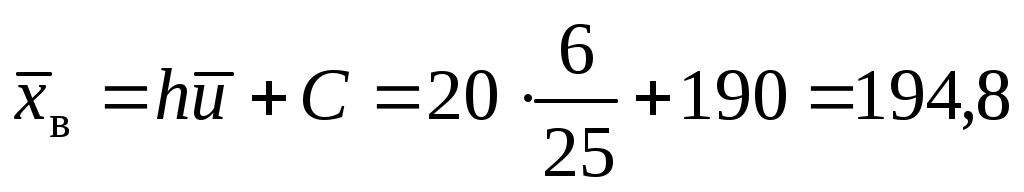 ;
;
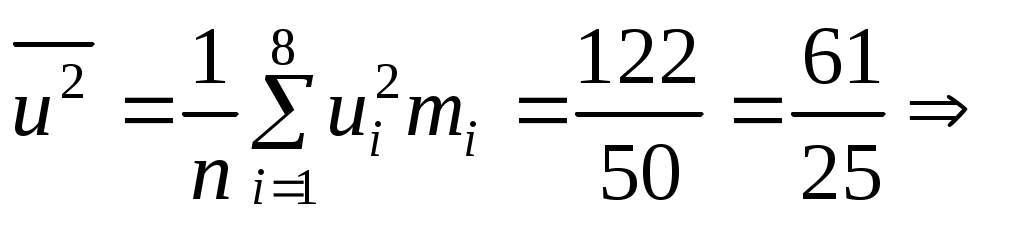
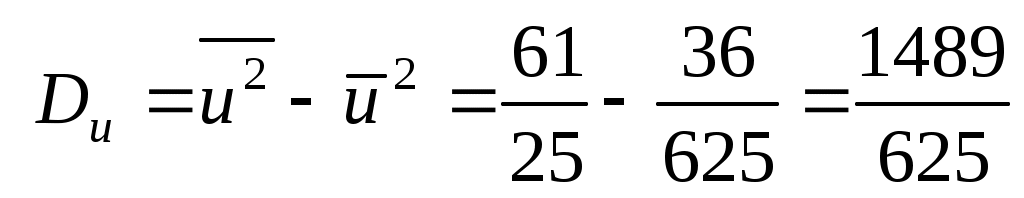 ;
;
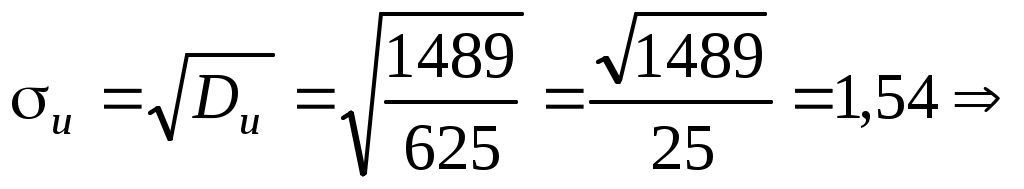
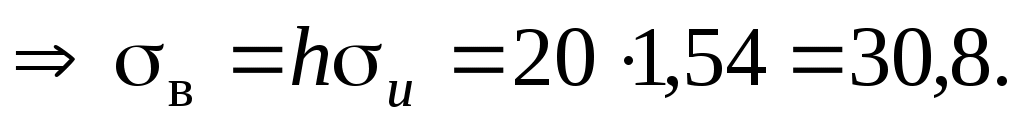
Найдем теоретические частоты (табл.3) для интервалов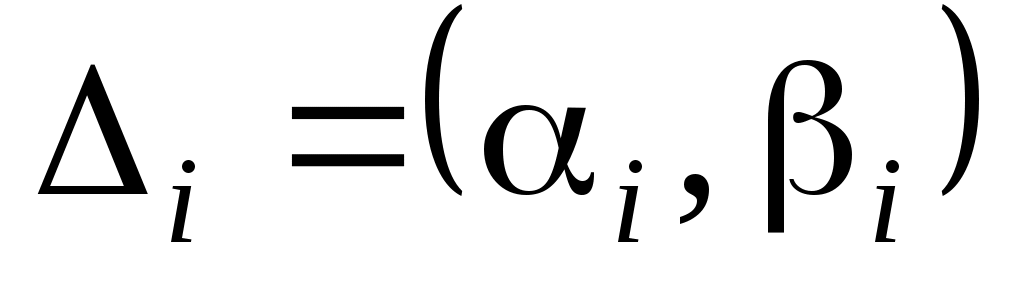 , используя формулу вероятности попадания значений в этот интервал (для нормального распределения с параметрами
, используя формулу вероятности попадания значений в этот интервал (для нормального распределения с параметрами 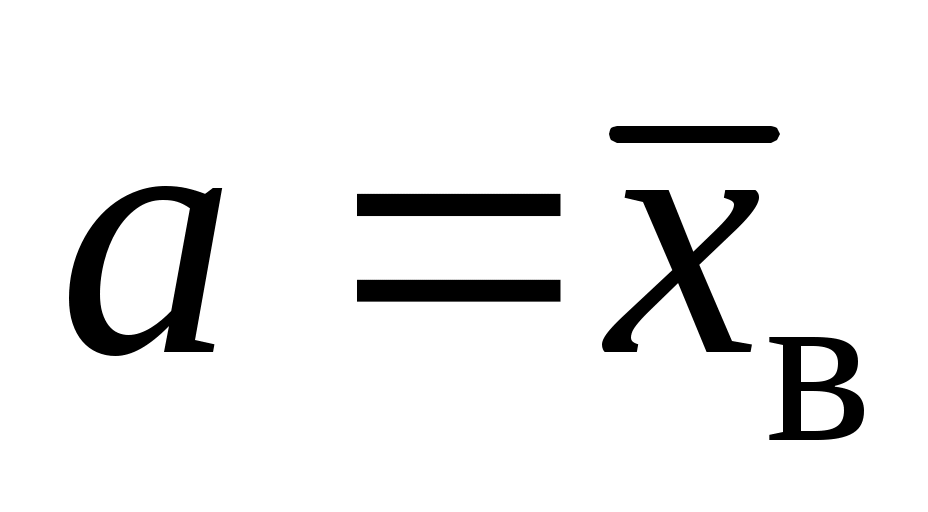 и
и 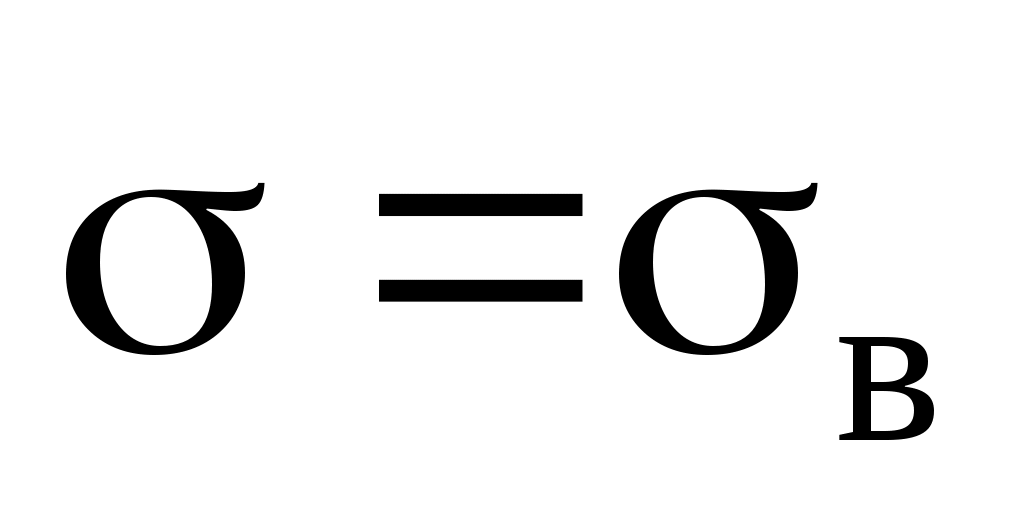 ):
):
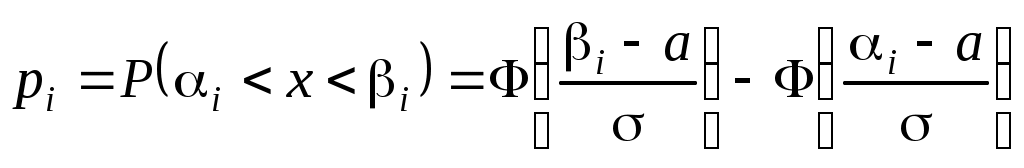 .
.
Таблица 3
Найдем выборочное значение , объединив крайние интервалы для маленьких частот mi (табл.4). Это объединение не является необходимым, но вполне применимо для упрощения в случае маленьких частот.
, объединив крайние интервалы для маленьких частот mi (табл.4). Это объединение не является необходимым, но вполне применимо для упрощения в случае маленьких частот.
Таблица 4
Таким образом, если после объединения число интервалов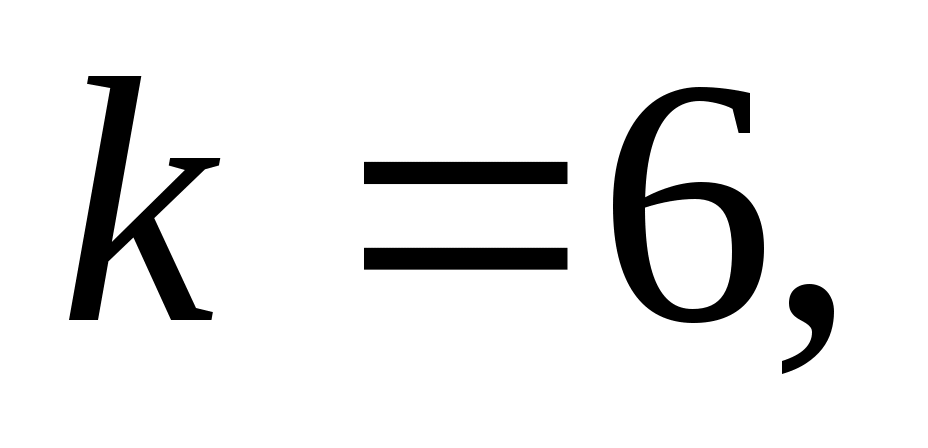 а число наложенных связей
а число наложенных связей  , то число степеней свободы
, то число степеней свободы 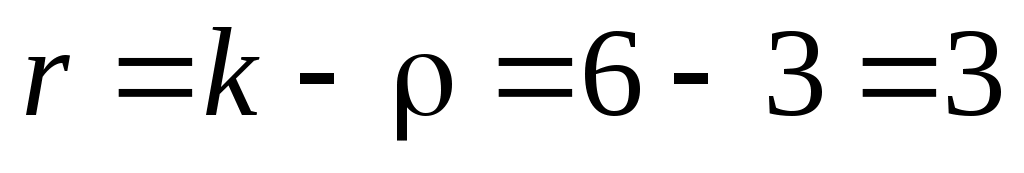 . Поэтому по таблице критических значений
. Поэтому по таблице критических значений
 (прил.3) имеем
(прил.3) имеем 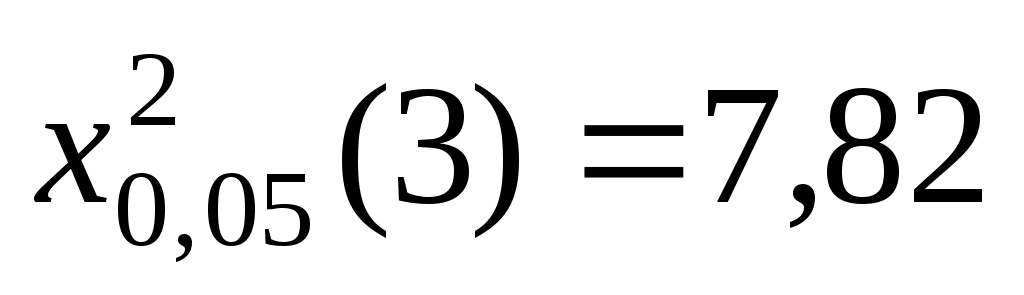 . Сравнивая найденное значение
. Сравнивая найденное значение 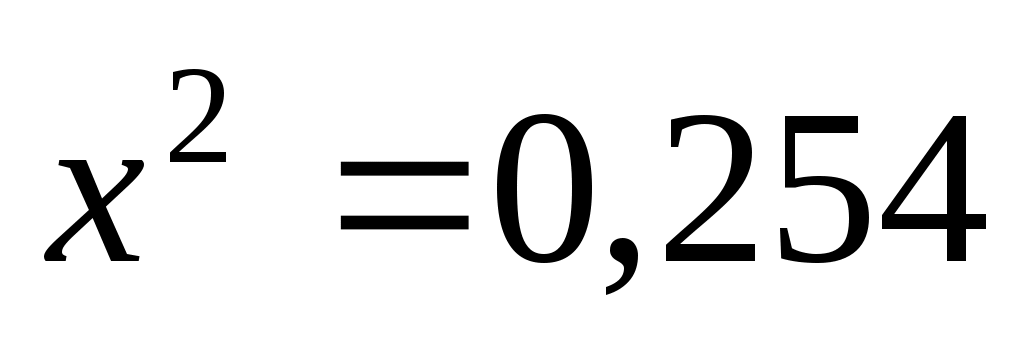 с критическим (0,254 < 7,82), получим, что рассматриваемые данные могут быть из нормально распределенной совокупности.
с критическим (0,254 < 7,82), получим, что рассматриваемые данные могут быть из нормально распределенной совокупности.
Для получения интервальной оценки найдем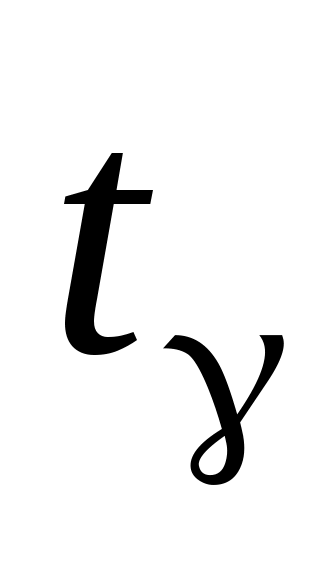 из условия
из условия 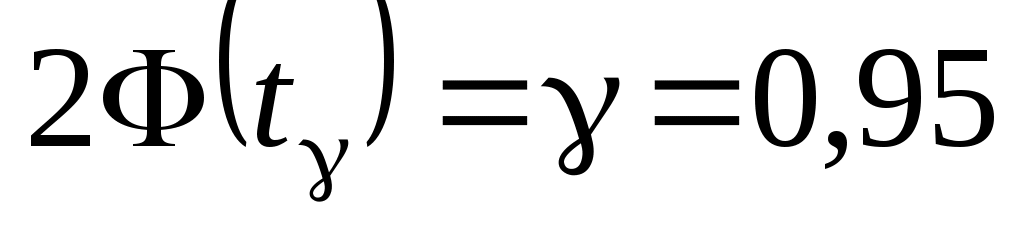 , т.е.
, т.е. 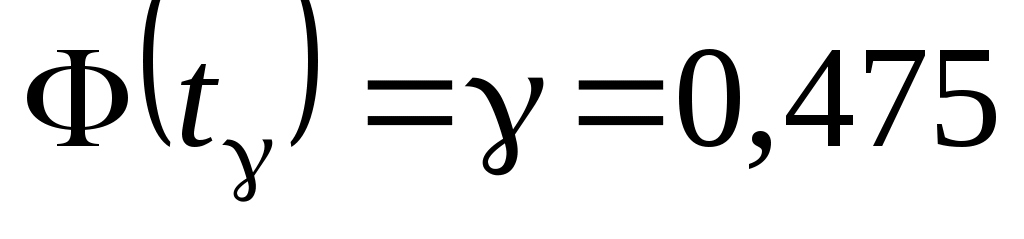 и
и 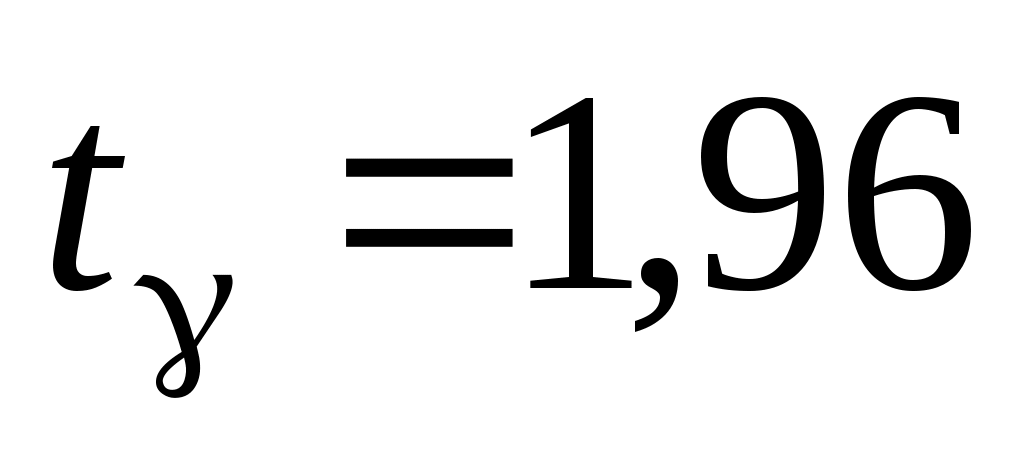 , и радиус интервала
, и радиус интервала 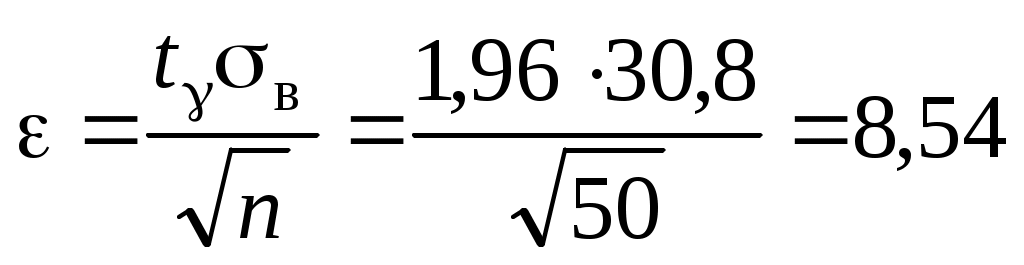 .
.
Вычислим доверительный интервал для параметра с надежностью
с надежностью  :
:
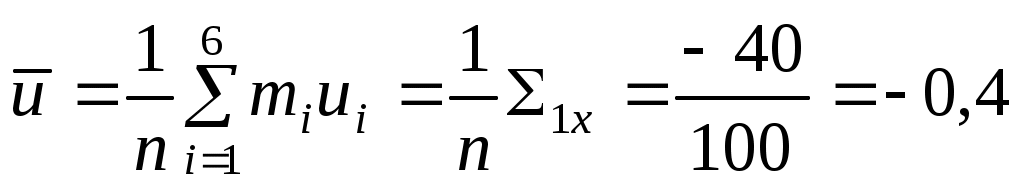 .
.
Пусть для изучаемой системы случайных величин (X, Y) получена выборка значений системы (xi, yi) с соответствующими совместными частотами mij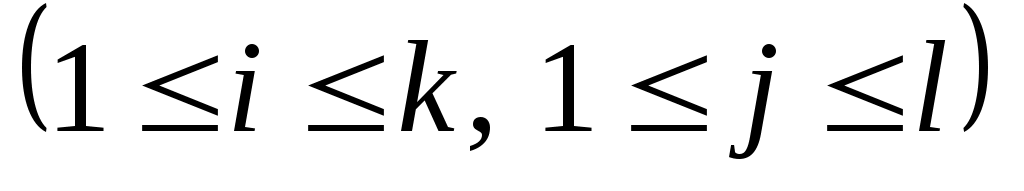 . Объем выборки
. Объем выборки 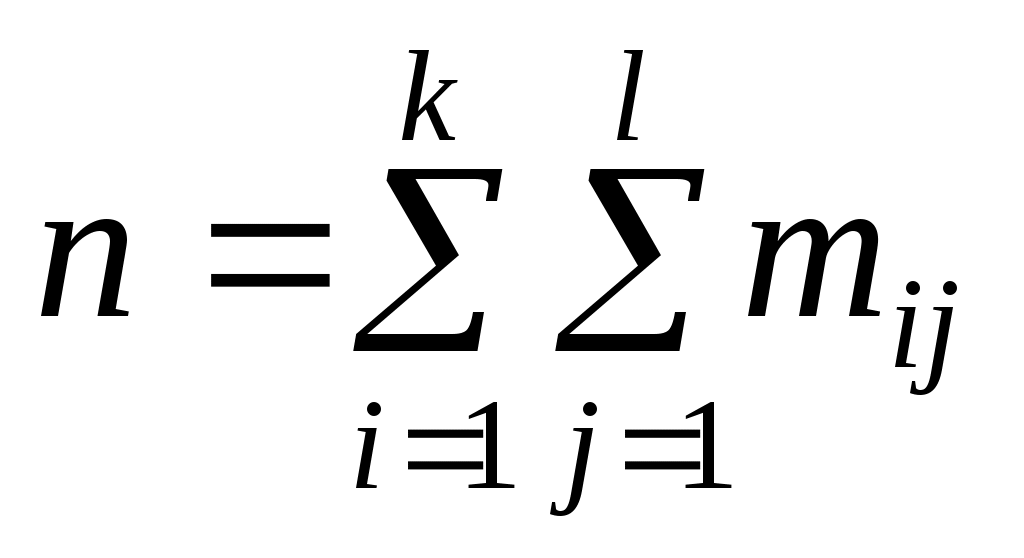 , каждое значение xi встречается с частотой
, каждое значение xi встречается с частотой 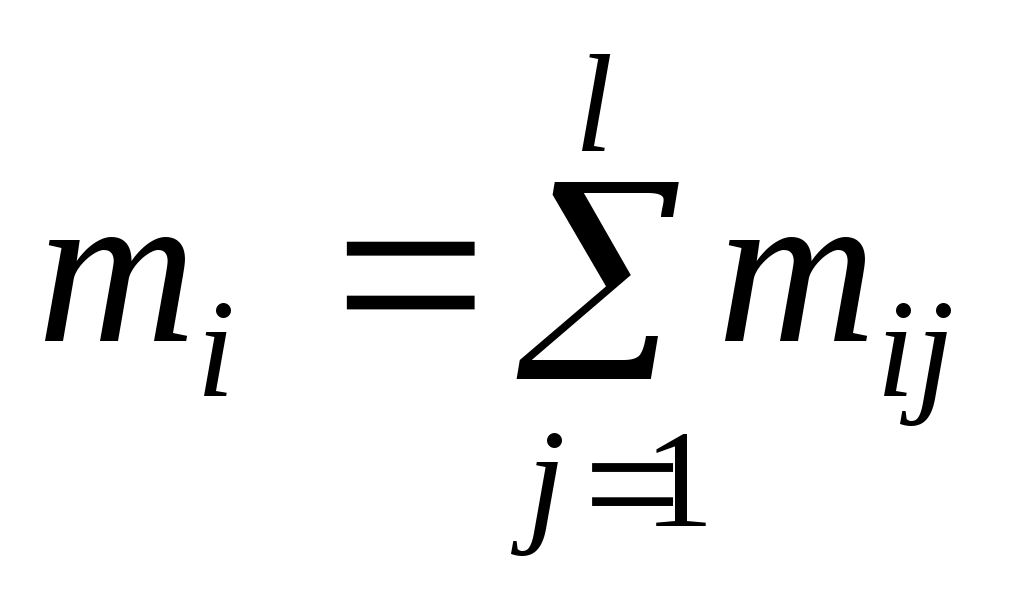 , а каждое значение yj встречается, соответственно, с частотой
, а каждое значение yj встречается, соответственно, с частотой 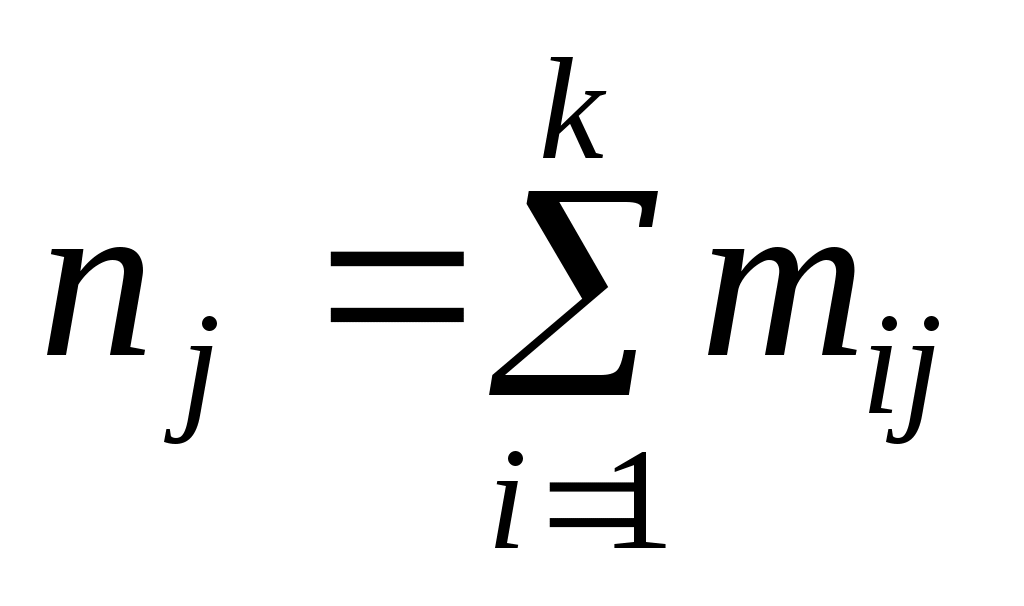 . Условные средние
. Условные средние 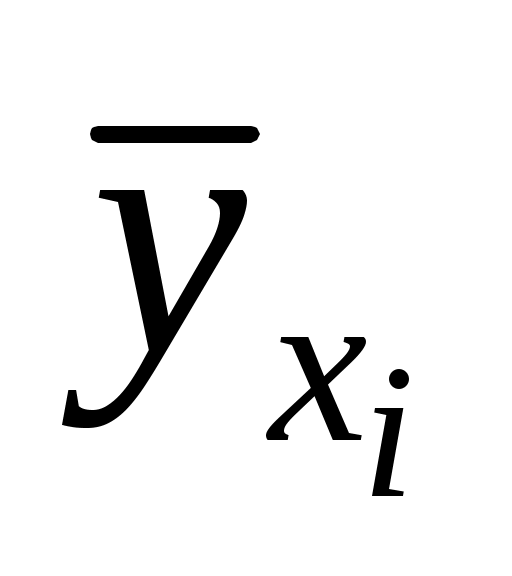 и
и 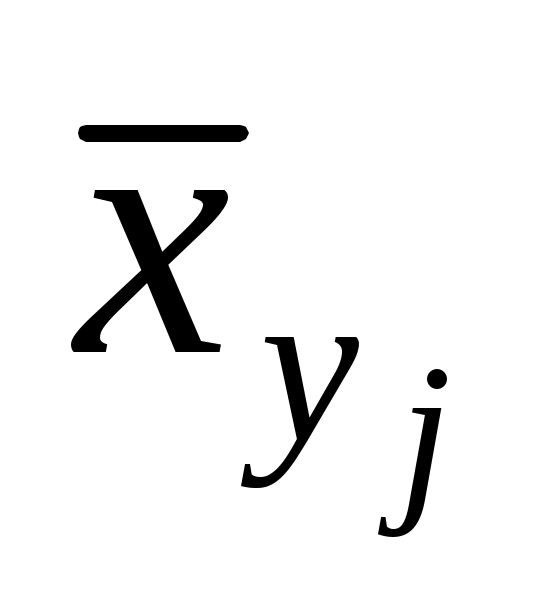 представляют отдельные значения для регрессий соответственно Y на X и X на Y:
представляют отдельные значения для регрессий соответственно Y на X и X на Y:
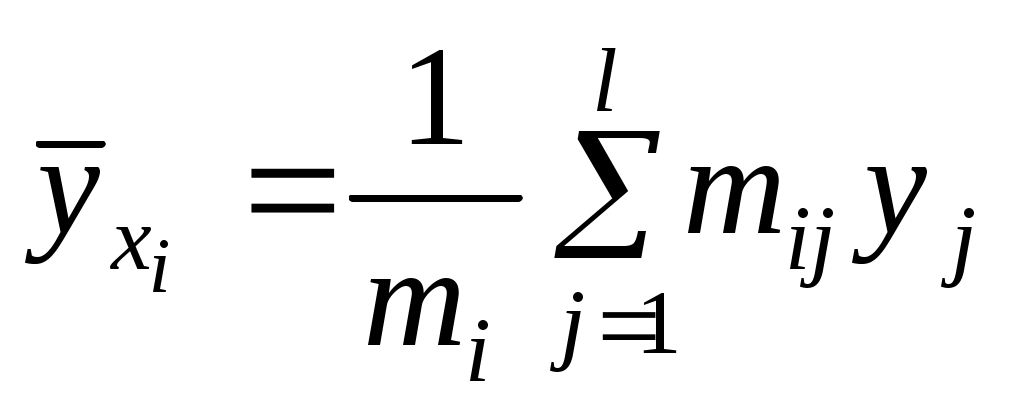 ,
, 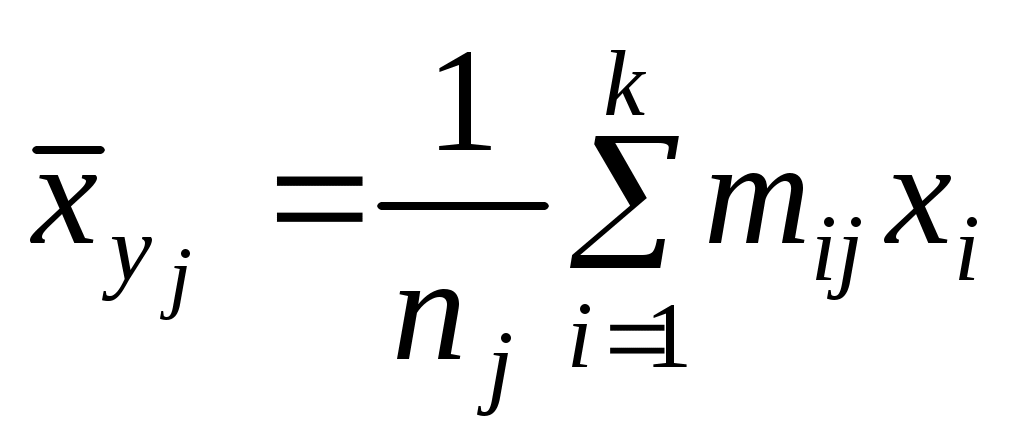 (
(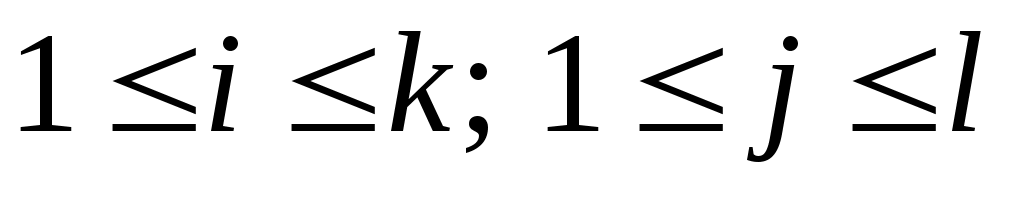
Отметим, что при использовании критерия Пирсона значения, частоты которых малы
Пример 15. При проведении испытаний материала на разрыв получено 50 значений, характеризующих прочность на разрыв. По этим данным составлен сгруппированный вариационный ряд (масштаб 104 Па).
| Интервал i | 120-140 | 140-160 | 160-180 | 180-200 | 200-220 | 220-240 | 240-260 | 260-280 |
| xi | 130 | 150 | 170 | 190 | 210 | 230 | 250 | 270 |
| mi | 2 | 4 | 10 | 13 | 11 | 6 | 3 | 1 |
Оценить согласие полученных данных с нормальным распределением при уровне значимости
Решение. Введем условную варианту, определив шаг h = 20 и выбрав ложный нуль C = 190, и найдем
Таблица 2
| Интервал i | xi | mi | | | | |
| | | | | | | |
| 1 | 130 | 2 | –3 | –6 | 9 | 18 |
| 2 | 150 | 4 | –2 | –8 | 4 | 16 |
| | | | | | | |
| 3 | 170 | 10 | –1 | –10 | 1 | 10 |
| 4 | 190 | 13 | 0 | 0 | 0 | 0 |
| 5 | 210 | 11 | 1 | 11 | 1 | 11 |
| 6 | 230 | 6 | 2 | 12 | 4 | 24 |
| 7 | 250 | 5 | 3 | 9 | 9 | 27 |
| 8 | 270 | 1 | 4 | 4 | 16 | 16 |
| __________ | | 50 | | 12 | | 122 |
По данным табл.2 имеем n = 50 и
Найдем теоретические частоты (табл.3) для интервалов
Таблица 3
| i | | | | | | |
| | | | | | | |
| 120-140 | –2,43 | –1,78 | –0,4924 | 0,4624 | 0,0300 | 1,5 1 |
| 140-160 | –1,78 | –1,13 | –0,4624 | –0,3708 | 0,0916 | 4,58 5 |
| 160-180 | –1,13 | –0,48 | –0,3708 | –0,1844 | 0,1864 | 9,34 9 |
| 180-200 | –0,48 | 0,17 | –0,1844 | 0,0675 | 0,2519 | 12,59 13 |
| 200-220 | 0,17 | 0,81 | 0,0675 | 0,2910 | 0,2235 | 11,17 11 |
| 220-240 | 0,81 | 1,46 | 0,2910 | 0,4279 | 0,1369 | 6,87 7 |
| 240-260 | 1,46 | 2,11 | 0,4279 | 0,4826 | 0,0547 | 2,78 3 |
| 260-280 | 2,11 | 2,73 | 0,4826 | 0,4968 | 0,0142 | 0,71 1 |
Найдем выборочное значение
Таблица 4
| Номер интервала | | mi | npi | mi – npi | (mi – npi)2 | |
| 1 | 120-140 | | 6 | 0 | 0 | 0 |
| 2 | 140-160 | |||||
| 3 | 160-180 | 10 | 9 | 1 | 1 | 0,111 |
| 4 | 180-200 | 13 | 13 | 0 | 0 | 0 |
| 5 | 200-220 | 11 | 11 | 0 | 0 | 0 |
| 6 | 220-240 | 6 | 7 | – | 1 | 0,143 |
| 7 | 240-260 | | 4 | 0 | 0 | 0 |
| 8 | 260-280 |
Таким образом, если после объединения число интервалов
Для получения интервальной оценки найдем
Вычислим доверительный интервал для параметра
Пусть для изучаемой системы случайных величин (X, Y) получена выборка значений системы (xi, yi) с соответствующими совместными частотами mij