ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 172
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
).
По выборке системы СВ определяют выборочные наилучшие линейные регрессии, которые приближенно выражают регрессионную (или корреляционную) зависимость между рассматриваемыми в системе случайными величинами:
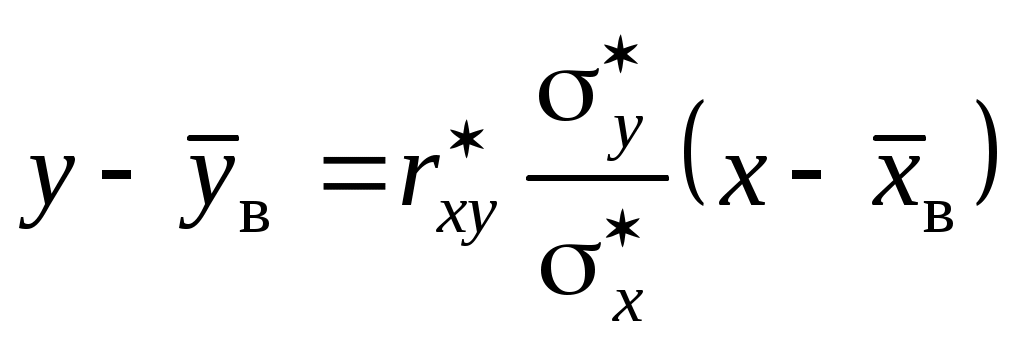 ,
, 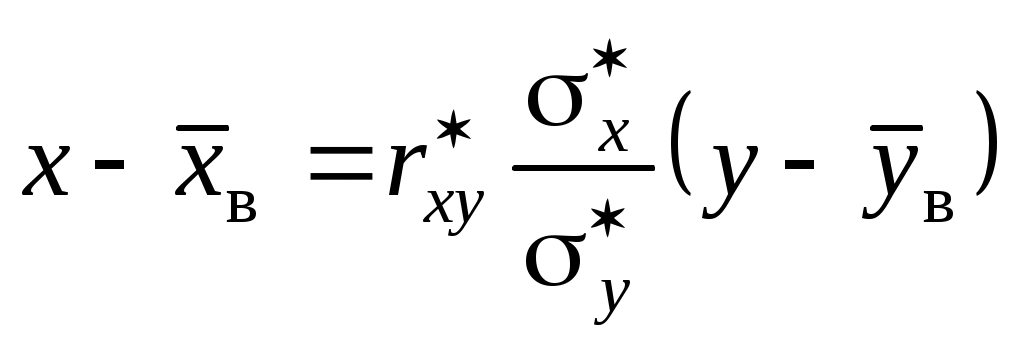 ,
,
где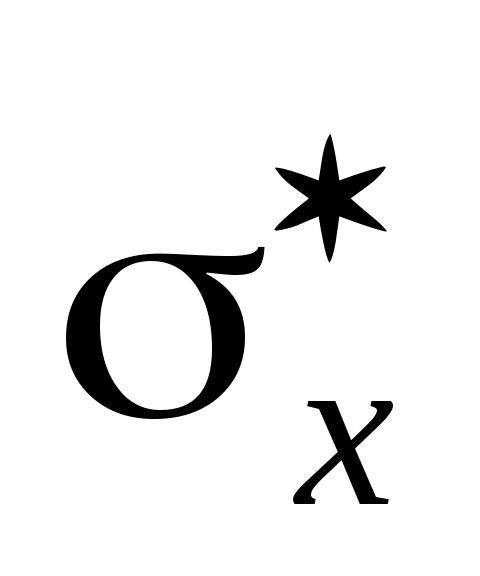 ,
,  – выборочные отклонения для X и Yсоответственно. выборочный коэффициент корреляции
– выборочные отклонения для X и Yсоответственно. выборочный коэффициент корреляции
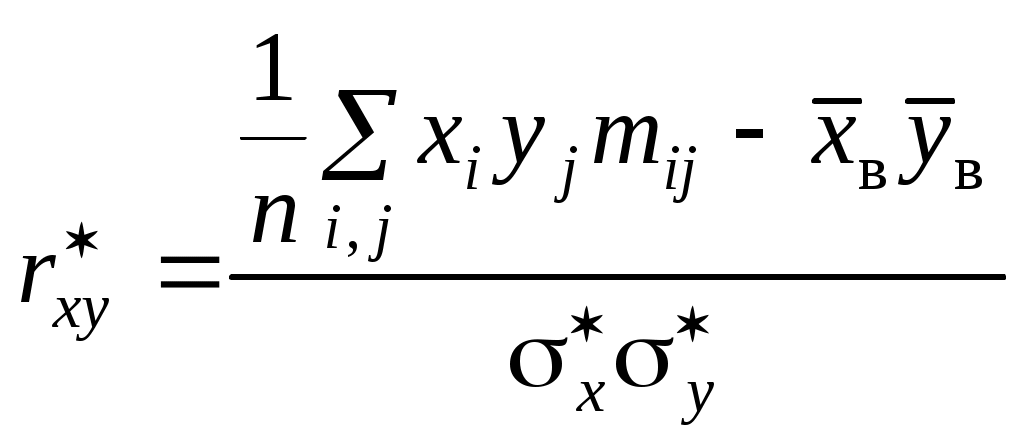 .
.
выборочные регрессии Y на X и X на Y приближают точки (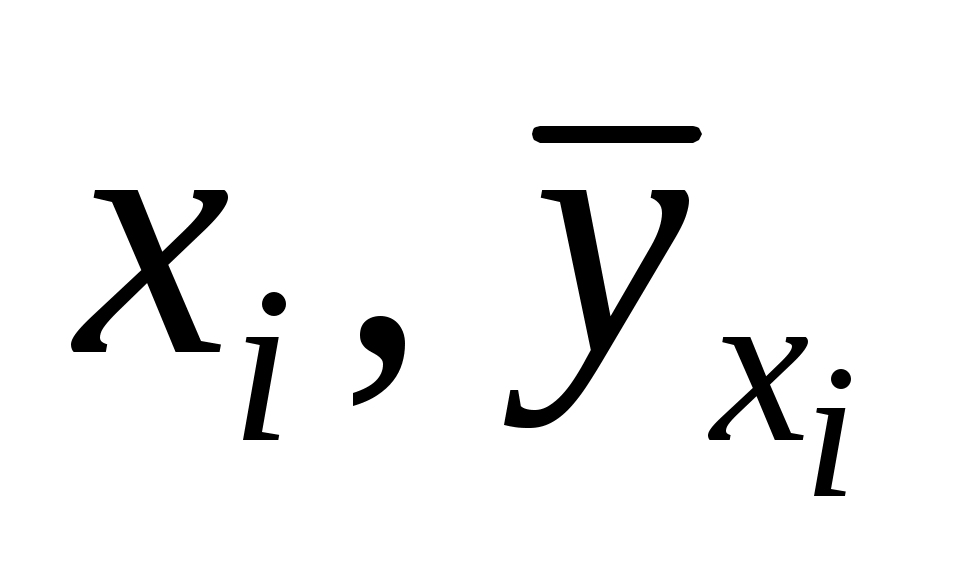 ) и (
) и (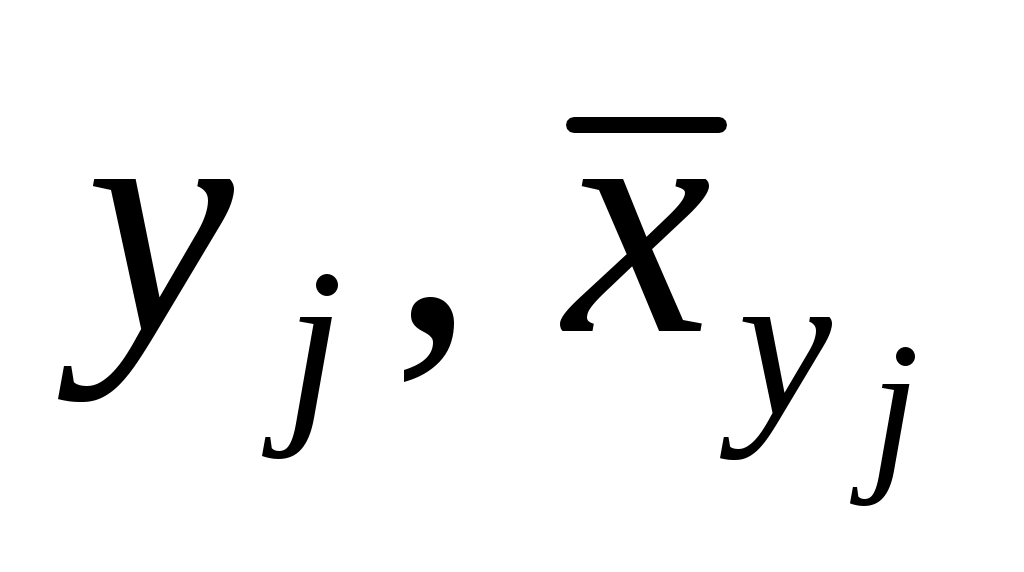 ) соответствующих условных средних
) соответствующих условных средних 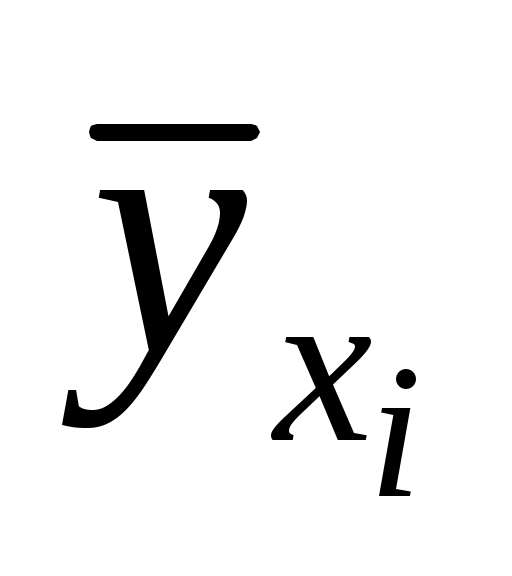 и
и 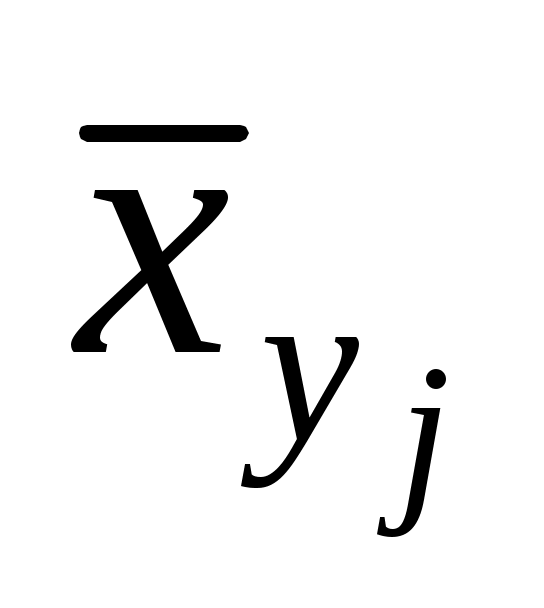 соответственно. По величине коэффициента
соответственно. По величине коэффициента 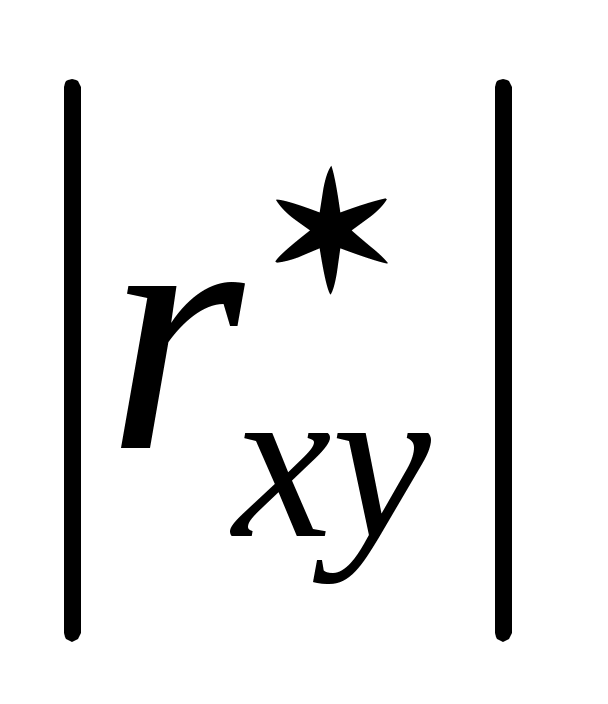 или по значению угла между прямыми выборочных регрессий можно сделать вывод о качестве связи между случайными величинами. Для расчета
или по значению угла между прямыми выборочных регрессий можно сделать вывод о качестве связи между случайными величинами. Для расчета 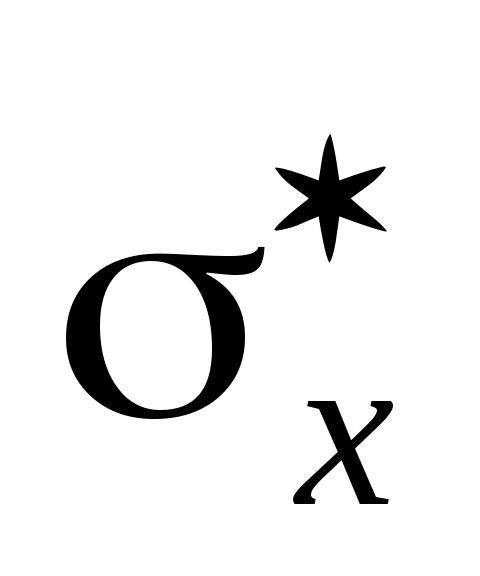 ,
, 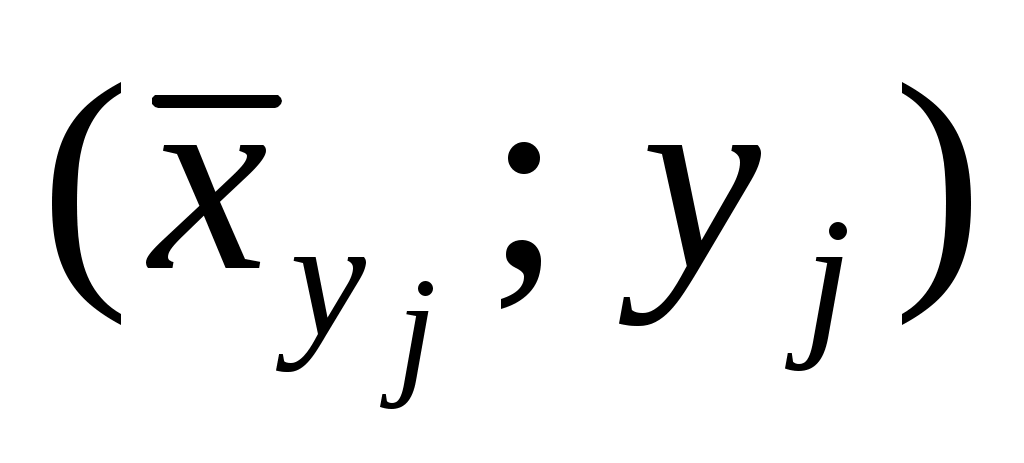 и
и 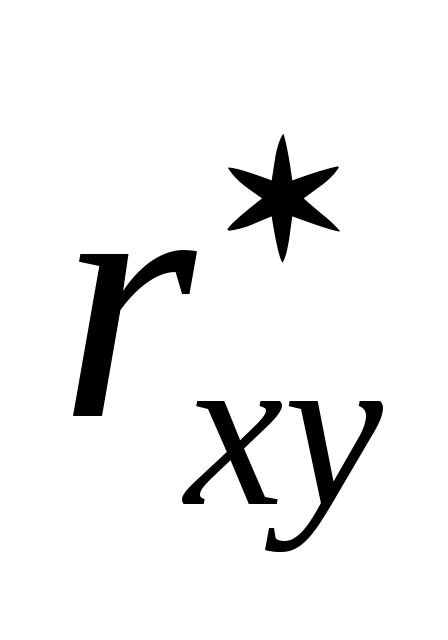 удобно использовать условные варианты для X и Y:
удобно использовать условные варианты для X и Y:
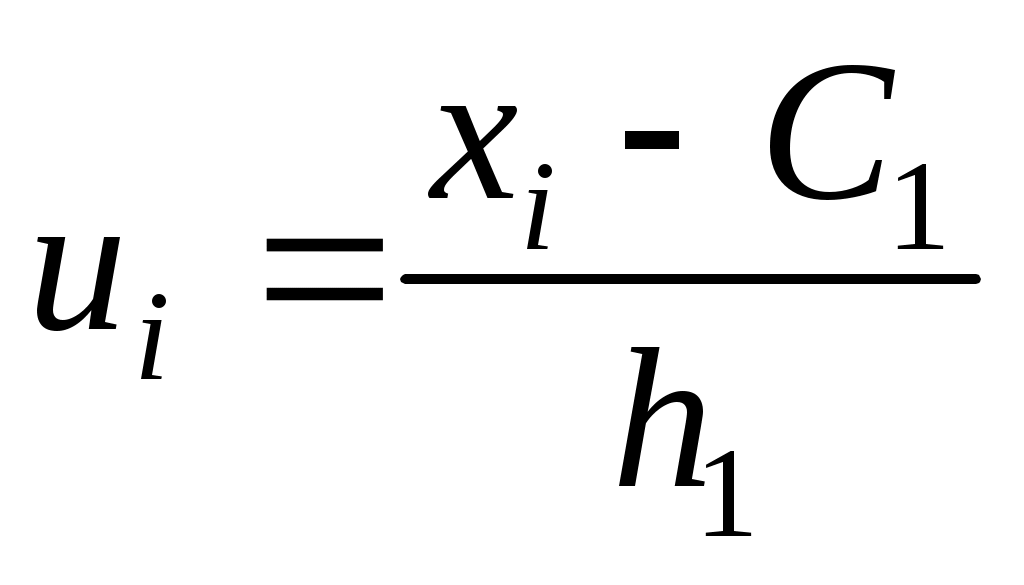 ,
, 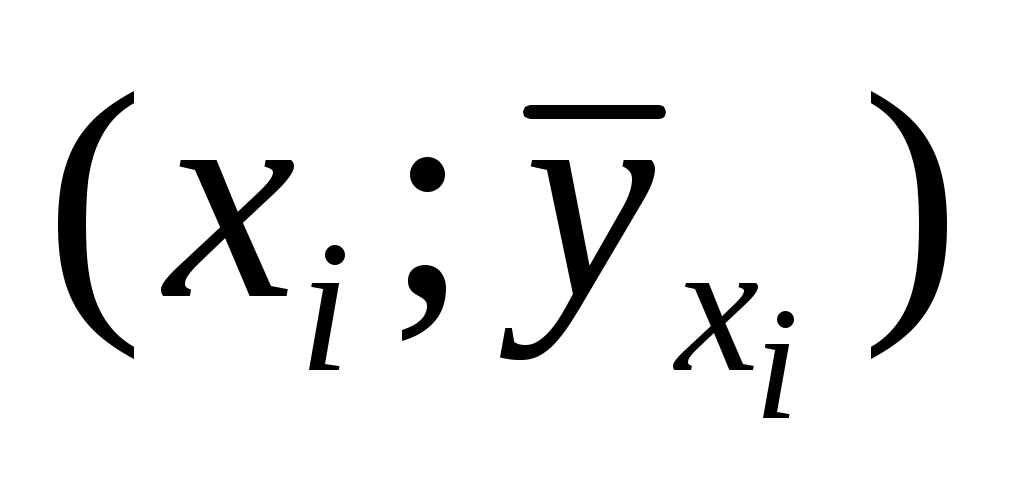 ,
, 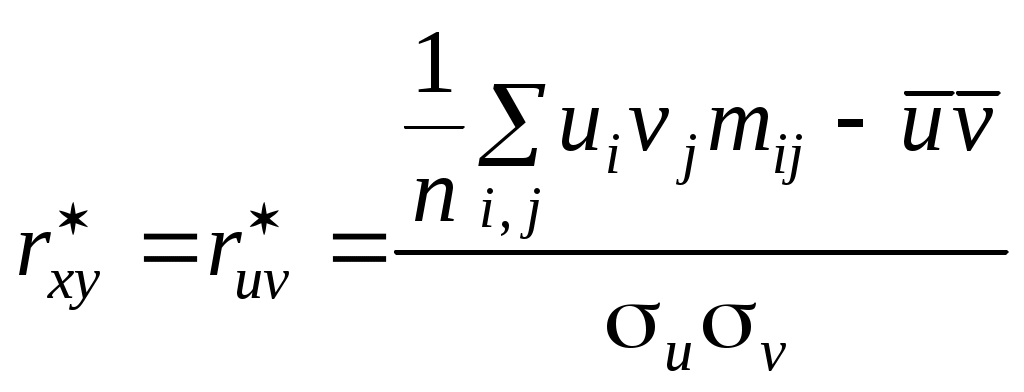 .
.
Пример 16. Пусть имеется 100 сгруппированных наблюдений двух измеримых признаков X и Y, по которым составлена корреляционная таблица (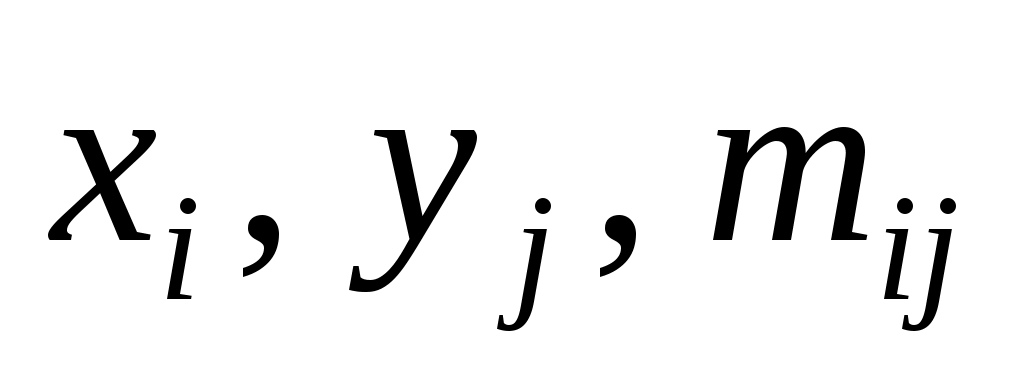 ) (табл.5).
) (табл.5).
Таблица 5
Найти выборочные регрессии и оценить качество связи признаков.
Решение. В табл.5 уже найдены отдельные частоты nj для yj (суммы частот mij по строкам), частоты mi для xi (сумма частот mij по столбцам) и условные средние. Например:
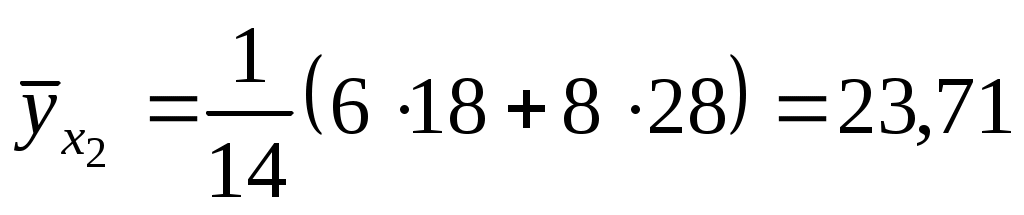 ,
, 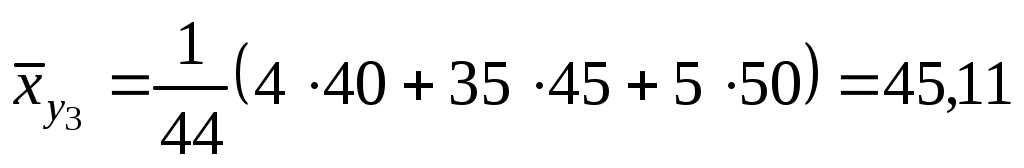 .
.
Соответствующие точки условных средних есть точки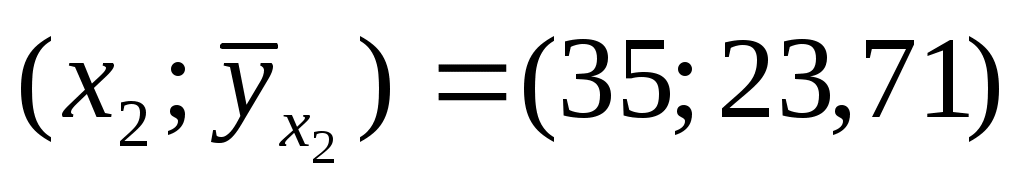 и
и 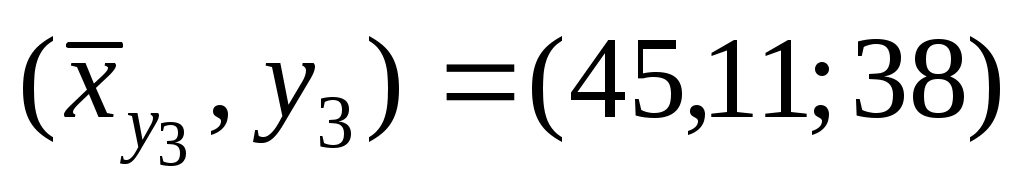 .
.
Для определения выборочных регрессий перейдем к условным вариантам.
Наибольшая частота, ближайшая к центру таблицы,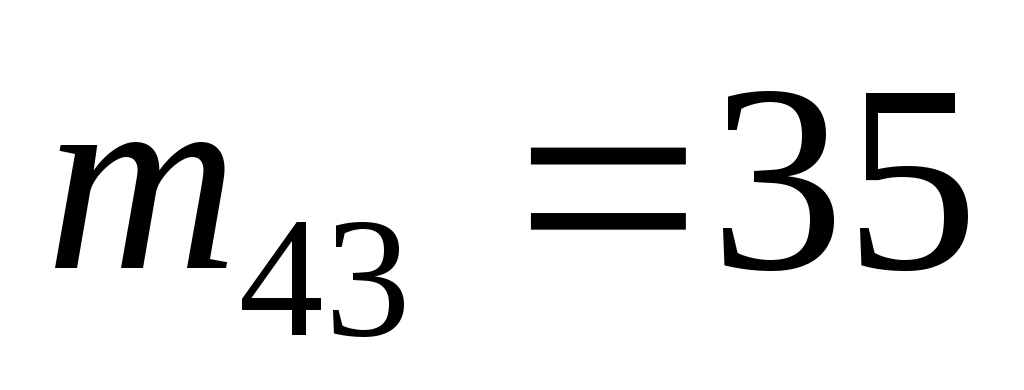 и, следовательно, соответствующие ложные нули
и, следовательно, соответствующие ложные нули 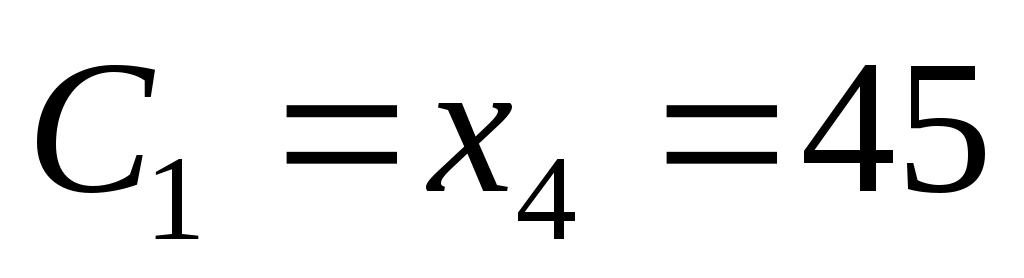 и
и 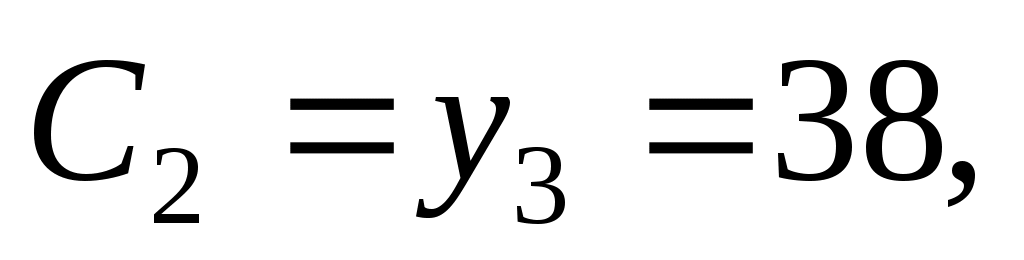 шаг
шаг 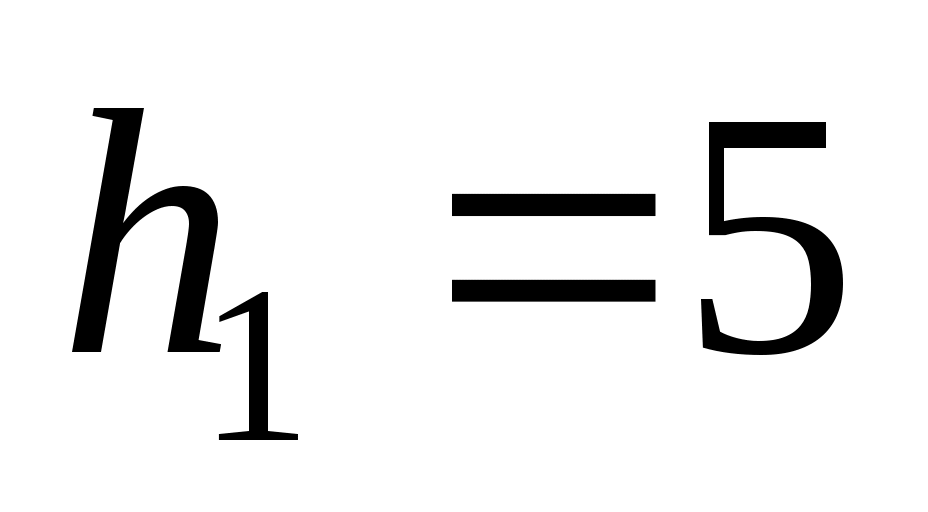 (для xi) и
(для xi) и 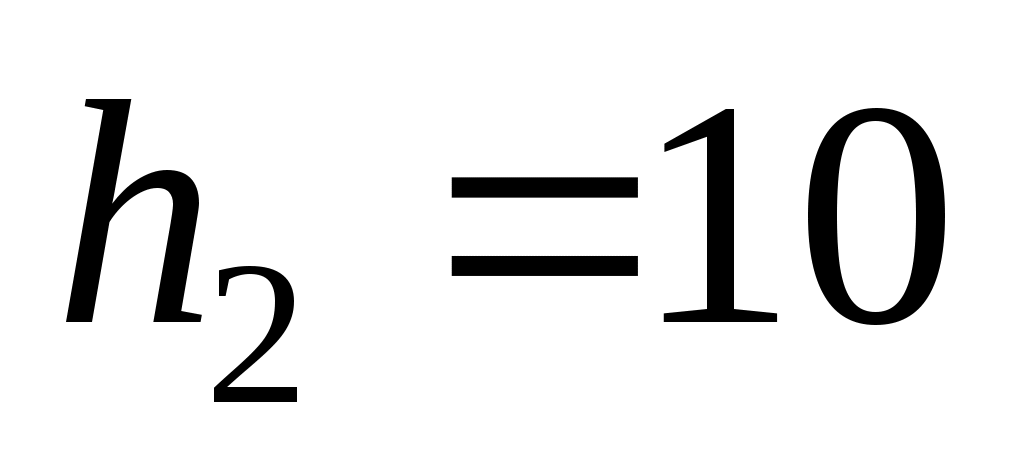 (для yj).
(для yj).
Составим новую таблицу в условных вариантах для расчета характеристик (табл.6).
Таблица 6
По данным табл.6 получим выборочные характеристики:
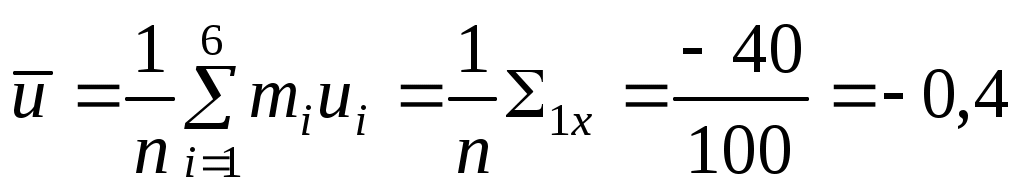 ;
;
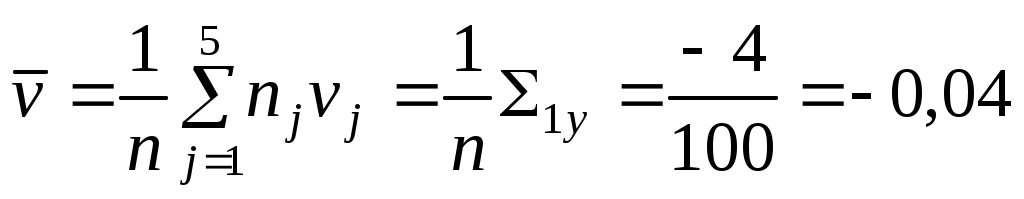 ;
;
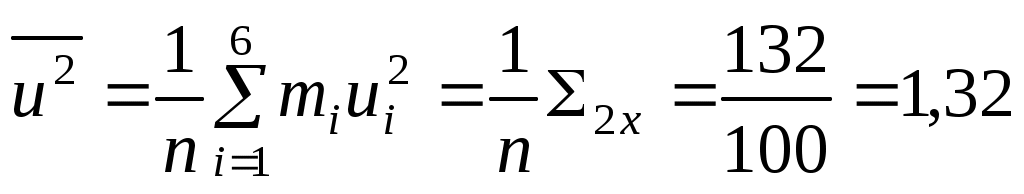 ;
;
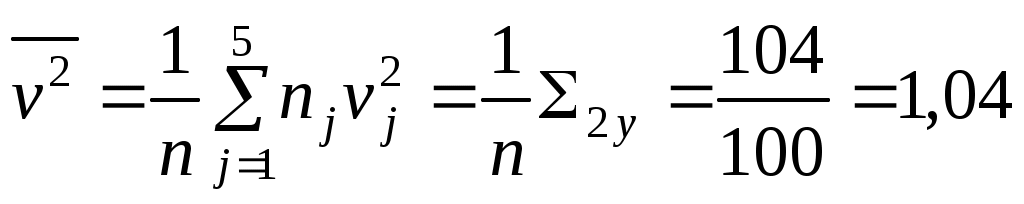 ;
;
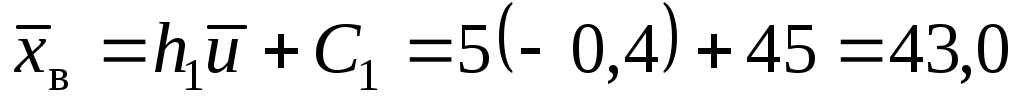 ;
;
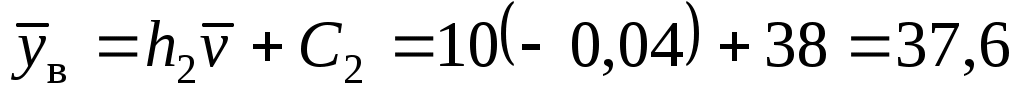 ;
;
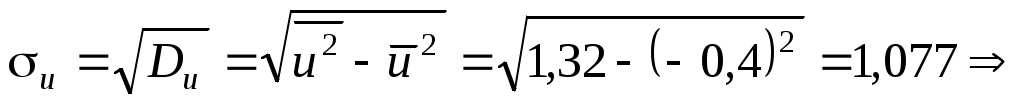
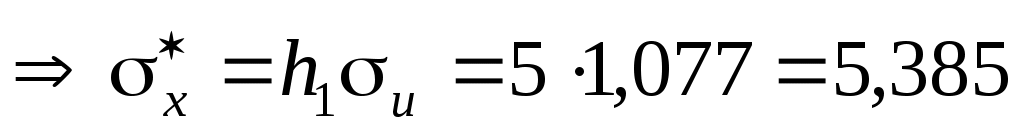 ;
;
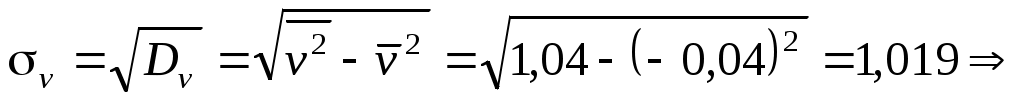
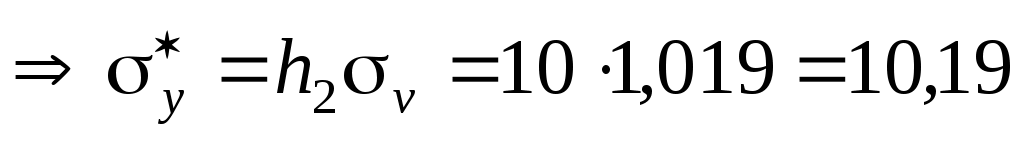 .
.
Для вычисления найдем средние суммы всех произведений uivjmij:
найдем средние суммы всех произведений uivjmij:
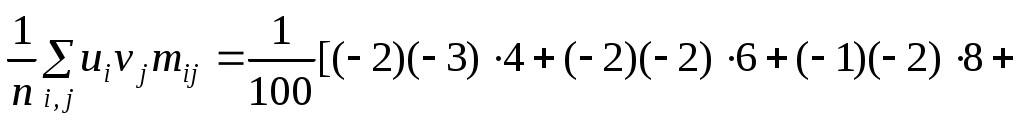
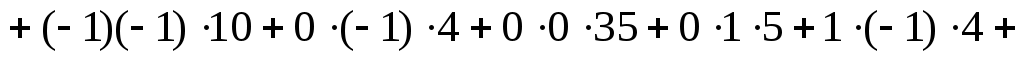
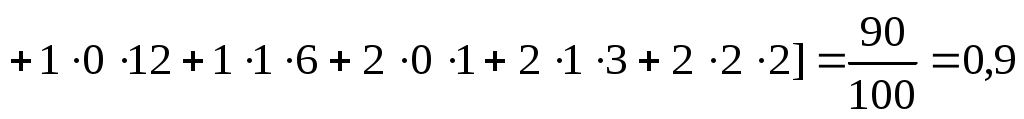 .
.
Выборочный коэффициент корреляции
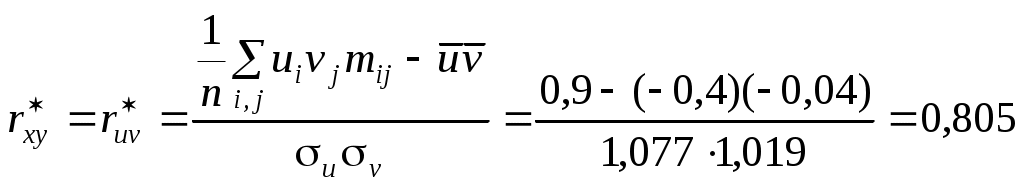 .
.
Уравнения выборочных регрессий имеют вид
для регрессии Y на X
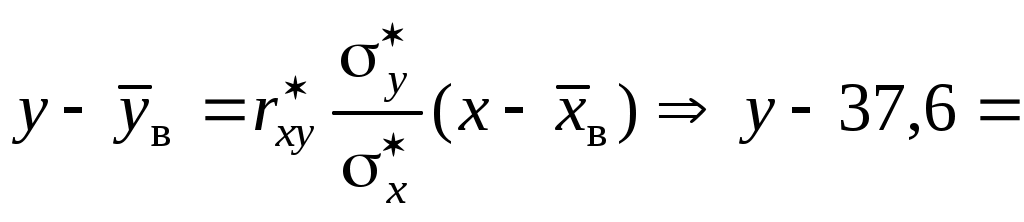
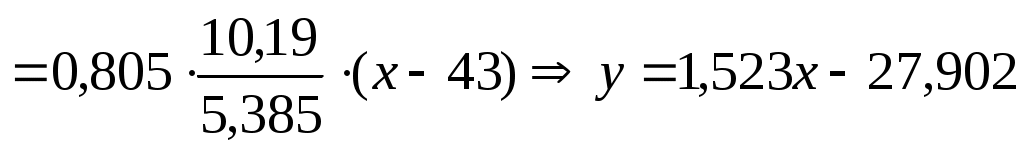 ;
;
для регрессии X на Y
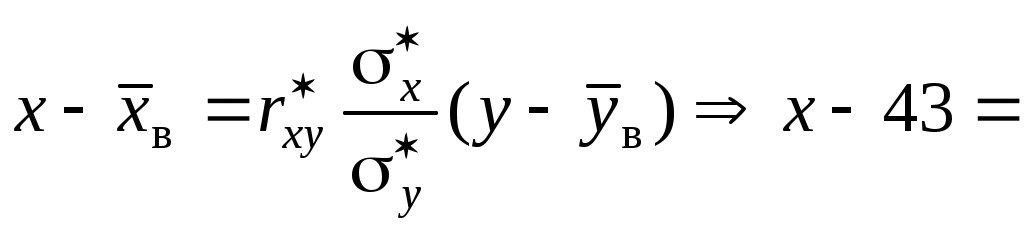
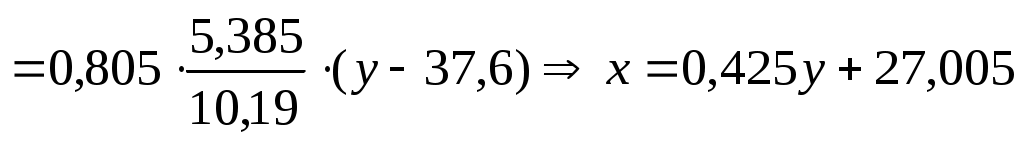 .
.
Обе прямых регрессий проходят через точку средних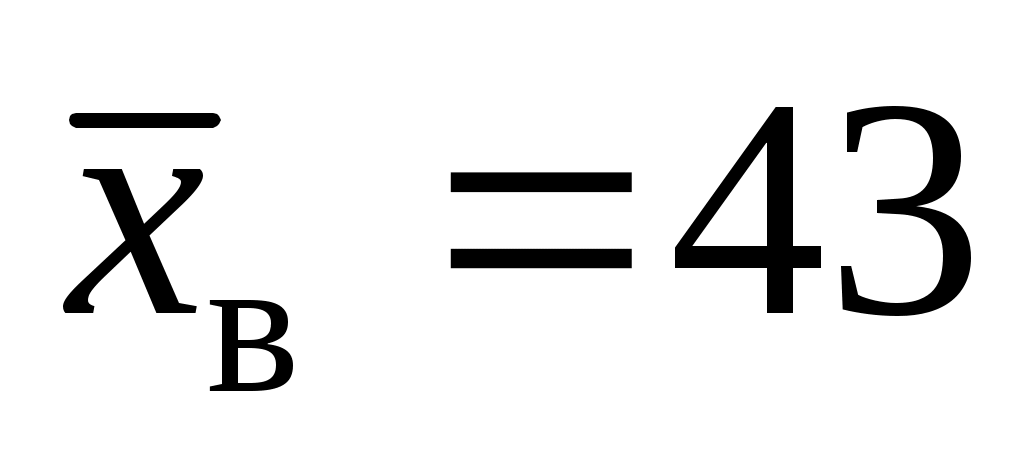
;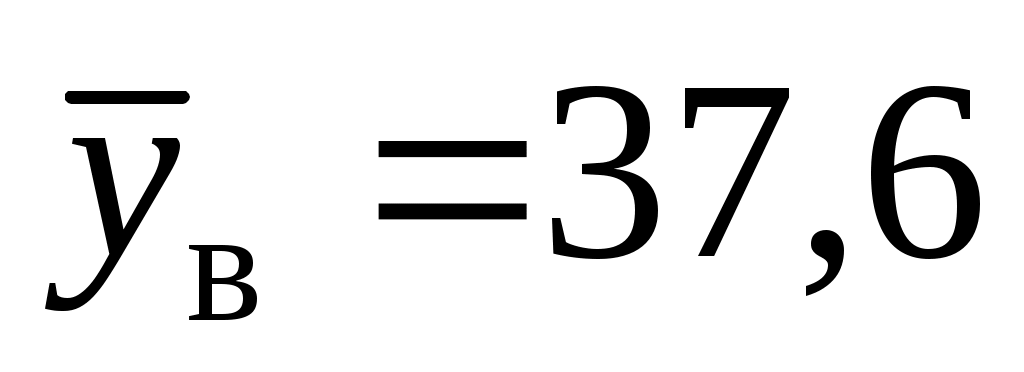 и для построения последних достаточно найти еще по одной точке для каждой прямой.
и для построения последних достаточно найти еще по одной точке для каждой прямой.
Так как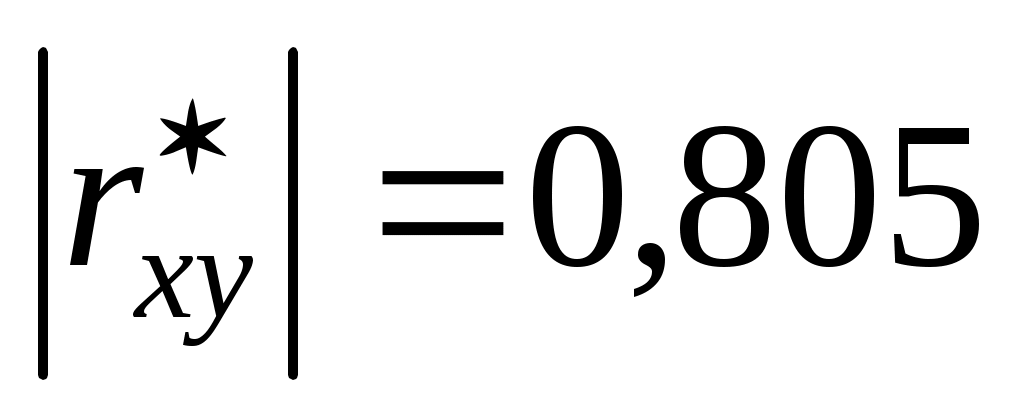 значительно отличаются от нуля, то связь между изучаемыми случайными величинами достаточно сильная, а так как это значение еще не близко к единице, связь нелинейная. Аналогичные выводы можно сделать и по величине угла между прямыми регрессий.
значительно отличаются от нуля, то связь между изучаемыми случайными величинами достаточно сильная, а так как это значение еще не близко к единице, связь нелинейная. Аналогичные выводы можно сделать и по величине угла между прямыми регрессий.
Для наглядности все точки условных средних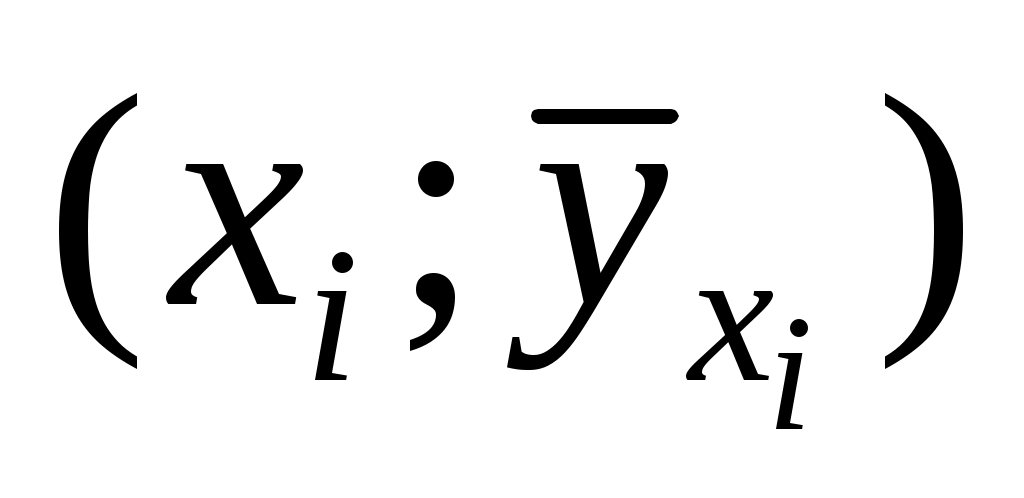 и
и 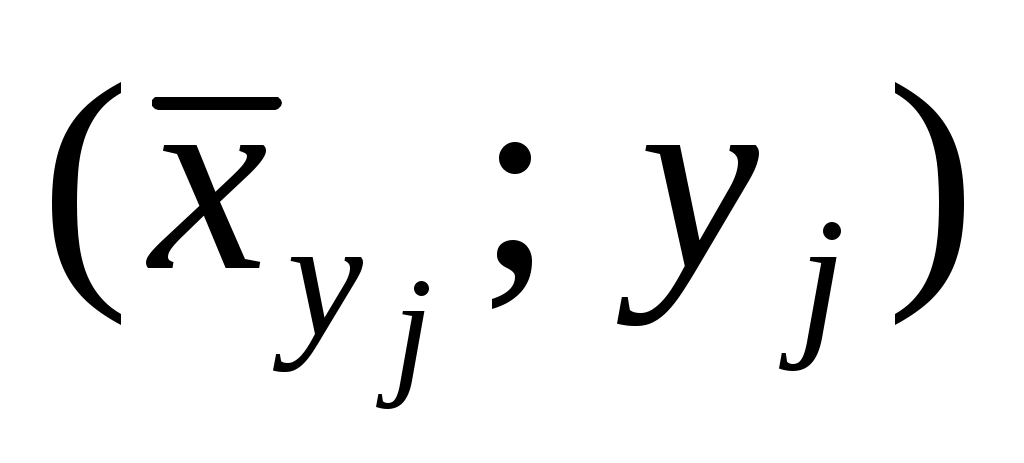 следует нарисовать на одном чертеже вместе с прямыми регрессий, причем масштаб на осях координат должен быть одинаков (чтобы избежать искажений).
следует нарисовать на одном чертеже вместе с прямыми регрессий, причем масштаб на осях координат должен быть одинаков (чтобы избежать искажений).
Задача1. В ящике имеются a белых и b черных шаров. Найти вероятность того, что:
а) первый вынутый из ящика шар будет белым;
б) все вынутые из ящика kшары будут черными.
Значения a,b и k по вариантам следующие:
Вариант 1. В ящике имеются 5 деталей, изготовленных на станке № 1, и 10 деталей, изготовленных на станке № 2. Сборщик последовательно вынимает из ящика детали одну за другой. Найти вероятность того, что во второй раз будет извлечена деталь, изготовленная на станке № 1.
Вариант 2. Из трех орудий одновременно произведен залп по цели. Вероятность попадания в цель при одном выстреле из первого орудия равна 0,9, для второго и третьего орудия эти вероятности соответственно равны 0,8 и 0,7.
Найти вероятность того, что:
а) только одно орудие попало в цель;
б) только два орудия попали в цель;
в) все три орудия попали в цель.
Вариант 3. Три автомата производят детали
По выборке системы СВ определяют выборочные наилучшие линейные регрессии, которые приближенно выражают регрессионную (или корреляционную) зависимость между рассматриваемыми в системе случайными величинами:
где
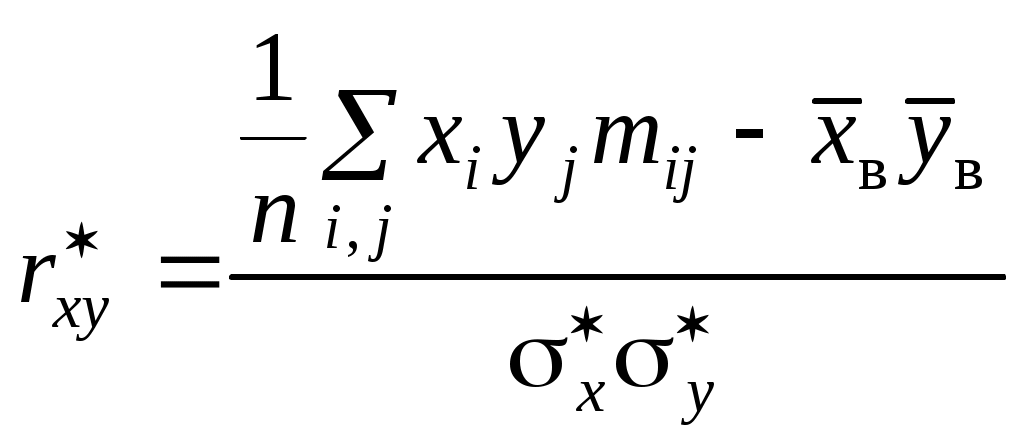 .
.выборочные регрессии Y на X и X на Y приближают точки (
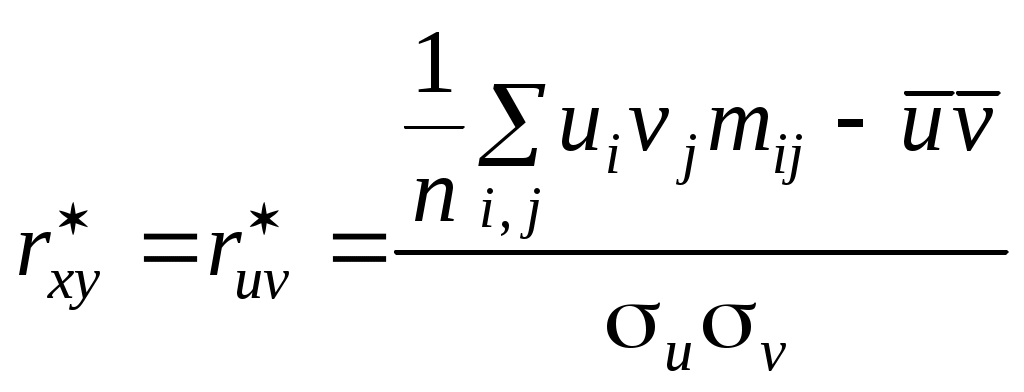 .
.Пример 16. Пусть имеется 100 сгруппированных наблюдений двух измеримых признаков X и Y, по которым составлена корреляционная таблица (
Таблица 5
| Y | X | nj | | |||||
| 30 | 35 | 40 | 45 | 50 | 55 | | | |
| | | | | | | | | |
| 18 28 38 48 58 | 4 | 6 8 | 10 4 4 | 35 12 1 | 5 6 3 | 2 | 10 18 44 22 6 | 33,0 37,78 45,11 45,45 50,83 |
| mi | 4 | 14 | 18 | 48 | 14 | 2 | n = 100 | |
| | 18,00 | 23,71 | 34,67 | 40,92 | 46,57 | 58,0 | | |
Найти выборочные регрессии и оценить качество связи признаков.
Решение. В табл.5 уже найдены отдельные частоты nj для yj (суммы частот mij по строкам), частоты mi для xi (сумма частот mij по столбцам) и условные средние. Например:
Соответствующие точки условных средних есть точки
Для определения выборочных регрессий перейдем к условным вариантам.
Наибольшая частота, ближайшая к центру таблицы,
Составим новую таблицу в условных вариантах для расчета характеристик (табл.6).
Таблица 6
| | | ||||||||
| –3 | –2 | –1 | 0 | 1 | 2 | | | | |
| –2 | 4 | 6 | | | | | 10 | –20 | 40 |
| –1 | | 8 | 10 | | | | 18 | –18 | 18 |
| 0 | | | 4 | 35 | 5 | | 44 | 0 | 0 |
| 1 | | | 4 | 12 | 6 | | 22 | 22 | 22 |
| 2 | | | | 1 | 3 | 2 | 6 | 12 | 24 |
| | 4 | 14 | 18 | 48 | 14 | 2 | n = 100 | | |
| | –12 | –28 | –18 | 0 | 14 | 4 | | | |
| | 36 | 56 | 18 | 0 | 14 | 8 | | | |
По данным табл.6 получим выборочные характеристики:
Для вычисления
Выборочный коэффициент корреляции
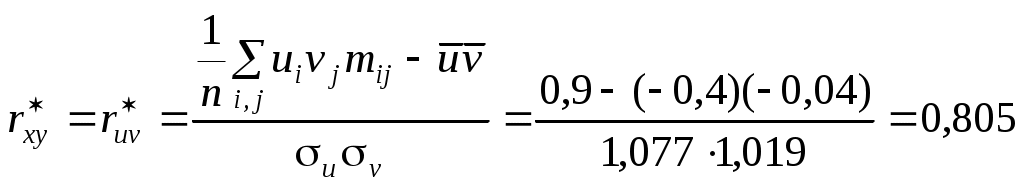 .
.Уравнения выборочных регрессий имеют вид
для регрессии Y на X
для регрессии X на Y
Обе прямых регрессий проходят через точку средних
;
Так как
Для наглядности все точки условных средних
КОНТРОЛЬНАЯ РАБОТА 6
Задача1. В ящике имеются a белых и b черных шаров. Найти вероятность того, что:
а) первый вынутый из ящика шар будет белым;
б) все вынутые из ящика kшары будут черными.
Значения a,b и k по вариантам следующие:
| Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| a | 6 | 3 | 5 | 10 | 4 | 6 | 3 | 5 | 8 | 7 |
| b | 5 | 7 | 8 | 5 | 66 | 8 | 7 | 10 | 4 | 5 |
| k | 3 | 4 | 2 | 3 | 4 | 5 | 3 | 4 | 3 | 3 |
Задача 2.
Вариант 1. В ящике имеются 5 деталей, изготовленных на станке № 1, и 10 деталей, изготовленных на станке № 2. Сборщик последовательно вынимает из ящика детали одну за другой. Найти вероятность того, что во второй раз будет извлечена деталь, изготовленная на станке № 1.
Вариант 2. Из трех орудий одновременно произведен залп по цели. Вероятность попадания в цель при одном выстреле из первого орудия равна 0,9, для второго и третьего орудия эти вероятности соответственно равны 0,8 и 0,7.
Найти вероятность того, что:
а) только одно орудие попало в цель;
б) только два орудия попали в цель;
в) все три орудия попали в цель.
Вариант 3. Три автомата производят детали