Файл: Дипломнаяработа по специальности 031200 педагогика и методика начального образования.doc

В тесной связи с изучением нумерации и арифметических действий формируется понятие о величинах и их измерении, ведется работа над простыми и составными задачами, рассмат­риваются числовые равенства и неравенства, простейшие урав­нения и неравенства с одной переменной. Учащиеся знакомятся с буквой как символом переменной, начинают оперировать бук­венными выражениями. Продолжается работа над геометрическим материалом: вводится прямой угол, прямоугольник, обозначение буквами точек, отрезков, углов, многоугольников, рас­сматривается ломаная, длина ломаной, периметр многоугольни­ка, решаются задачи с геометрическим содержанием. Всё это способствует овладению ими операцией сравнения и классификации.

Задача учителя при изучении этой темы - научить детей считать до 20, показать, как образуются числа из десятков и единиц, научить, читать и записывать двузначные числа на основе твердого знания о том, что единицы пишутся на первом, а десятки - на втором месте, считая справа налево. Необходимо также добиться усвоения учащимися новых понятий и терминов: единицы первого и второго разряда, разрядное число, сумма разрядных слагаемых, однозначное и двухзначное число, сформировать оперативное умение сравнивать и классифицировать.

В изучении нумерации выделяются две ступени: сначала изучается нумерация чисел 11 - 20. При написании только чисел второго десятка порядок называния составляющих их разрядных чисел и порядок записи не совпадает: сначала называются единицы (тринадцать), а пишется первым десяток (13). Эти особенности нумерации требуют того, чтобы числа второго десятка были рассмотрены отдельно.

Подготовительная работа к изучению нумерации чисел вто­рого десятка проводится при повторении материала по теме «Десяток». С этой целью включаются упражнения в счете пред­метов с выходом за десяток к примеру, сколько учеников в пер­вом ряду, во втором ряду? Так, например, можно предложить детям упражнения на развитие операции классификации и закрепления материала по теме «Десяток»: посмотрите на рисунок и определить общие признаки и свойства изображённых на нём предметах, чтобы получилось верным действие сложения.



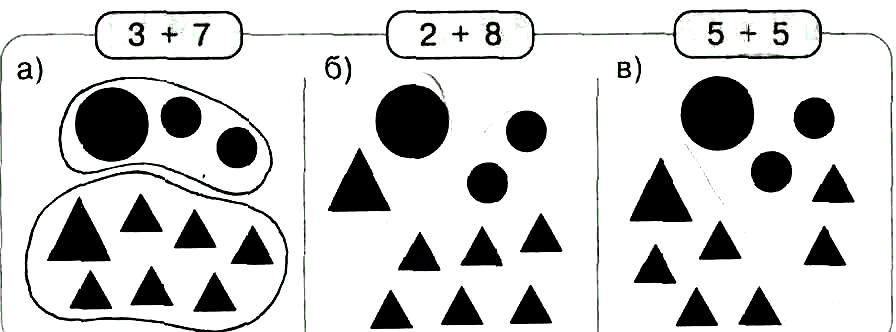
рис. 1

Изучение устной нумерации чисел второго десятка начинается с формирования у детей понятия о десятке. Отсчитывая по 10 палочек и завязывая их в пучки, учащиеся узнают, что десять единиц образуют десяток. Затем, выполняя упраж­нения в счете десятков палочек, сложении и вычитании десят­ков с использованием палочек, дети убеждаются, что десятки можно считать, складывать и вычитать как простые единицы.

---

Далее рассматривается образование чисел от 11 до 20 из десятков и единиц и поясняются их названия.

Например, упражнение: глядя на рис. 2, классифицировать по общему признаку изображённые на нём предметы: по цвету, форме, размеру.

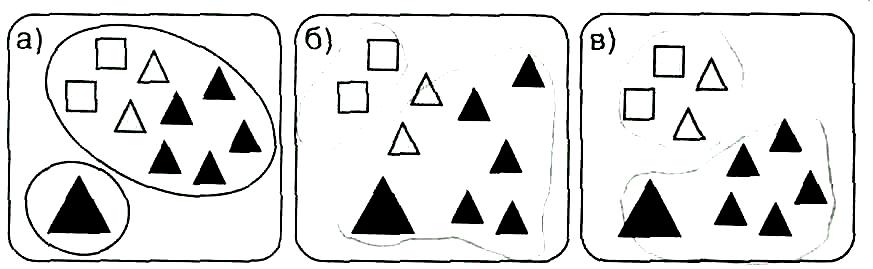Рис. 2

Мы предлагали учащимся положить 1 палочку на пу­чок-десяток палочек и посчитать, сколько всего палочек ста­ло. Затем, опираясь на иллюстрацию, дети устанавливали деся­тичный состав полученного числа. Далее вспоминали, как по­лучить следующее число, присоединяли к 11 палочкам еще 1 палочку и объясняли, что «две на десять» — это двенадцать, что число 12 состоит из 1 десятка и 2 единиц.

Так же мы рассматривали образование и название других чи­сел второго десятка и одновременно порядок их следования при счете.

Помимо палочек, в качестве наглядного пособия мы использовали полоски, на каждой из которых по 10 кружков (десятки), и по­лоски с 1, 2, 3, …, 9 кружками (единицы). При этом мы сравнивали их и классифицировали.

Натуральное следование чисел удобно иллюстрировать с по­мощью самодельных бумажных полосок длиной 20 см. Используя «ленту двадцати», дети устанавливают, ка­кое число за каким следует, какому предшествует, между каки­ми числами находится. Это формирует у них операцию сравнения. Например, каждый раз мы предлагали детям сравнить пучок-десяток и одну палочку с одиннадцатью отдельными палочками (двенадцатью, тринадцатью и т.д.).

Для закрепления знаний десятичного состава и натурального следования чисел в пределах 20 предлагают учащимся - сначала с опорой на наглядные пособия, а потом без них - такие упражнения: «Отсчитайте 15 палочек; узнайте, сколько это со­ставляет десятков палочек и сколько отдельных палочек; возьмите 1 десяток палочек и еще 4 палочки. Сколько всего палочек взяли? Сколько десятков и единиц в числе 17? Какое число состоит из 1 десятка и 9 единиц? Положите 13 палочек, придви­гайте теперь по одной палочке и называйте, сколько палочек ста­новится (до 20—25); положите 17 палочек; откладывайте в сто­рону по одной и называйте, сколько палочек остается (до 7—8); начиная с числа 10 присчитывайте по одному и называй­те полученные числа; отсчиты­вайте от 20 по одному, пока не получится 10».

Далее учащиеся знакомятся со второй единицей длины - дециметром как десятком санти­метров. Включаются упражнения в черчении и измерении отрезков, длина которых выражается как в единицах одного наименова­ния (12 см, 15 см и т. п.), так и в единицах двух наименований (1 дм 5 см, 1 дм 8 см и т. п.). Опираясь на сравнение отрезков, дети постепенно овладевают умениями заменять крупные еди­ницы мелкими (1 дм 3 см =13 см) и обратно (20 см =2 дм). При этом закрепляются знания десятичного состава. Например, 1 дм 3 см надо выразить в сантиметрах. Сравнивая, ученик рассуждает так: 1 дм—это 1 десяток сантиметров; 1 десяток и 3 см со­ставляют 13см. Аналогично выражая 15см в дециметрах и сан­тиметрах, в числе 15 см выделяют 1 десяток сантиметров (т.е. 1 дм) и 5 см. подобные приёмы проводились нами на каждом уроке при изучении нового числа в пределах 20.

---

На следующем этапе приступают к изучению письмен­ной нумерации. Чтобы раскрыть поместный принцип записи двузначных чисел, используют абак-таблицу с двумя рядами карманов: один ряд – 6 для палочек, другой - для раз­резных цифр. Знакомя с пособием, учитель показы­вает, как ставят в верхних карманах палочки, когда их 5, 9, 10, 14 штук. Затем ученикам предлагают разложить в карманы, например, 15, 17 палочек.

Переходя к обозначению чисел, обязательно выясняют деся­тичный состав каждого числа и, опираясь на него, записывают, цифрами, сколько в этом числе десятков и сколько, кроме того, единиц. Сразу закрепляют полученные знания о принципе за­писи двузначных чисел: что обозначает цифра 7, которая стоит в записи числа 17 на первом месте справа, и что обозначает циф­ра 1, которая стоит на втором месте справа.

Аналогично рассматривают еще несколько чисел, а затем де­ти записывают числа в своих тетрадях в таблицах с надписями «десятки» и «единицы» и объясняют значение каждой цифры.

Особо рассматривается запись чисел 10 и 20: цифра 1 (2) показывает, что в числе содержится 1 десяток (2 десятка), циф­ра 0 - в числе отсутствуют единицы.

Упражняясь в записи чисел, учащиеся закрепляют знания десятичного состава и натурального следования чисел в преде­лах 20. Например, учитель предлагает записать число, которое состоит и:) 1 десятка и 9 единиц; записать число, которое следует при счете за числом 19 (предшествует числу 11); которое больше (меньше) на 1 числа 15; решить примеры 12+1, 18-1 и записать ответы. Дети записывают ответы и объясняют, поче­му они записали то или иное число. Так, выполняя последнее за­дание, учащиеся поясняют: к 12 прибавить 1, получится 13, по­тому что, прибавляя к числу 1, получаем число, которое следует за ним при счете.

Опираясь на наглядные пособия, учащиеся знакомятся со случаями сложения и вычитания вида: 10+5, 15-5, 15-10. Вы­полняя такие вычисления, учащиеся закрепляют знания деся­тичного состава чисел: например, 10+5, десять - это 1 десяток, 1 десяток и 5 единиц составляют число 15; 15 - 10, пятнадцать - это 1 десяток и 5 единиц, вычтем 10, или 1 десяток, получится 5 единиц.

Сопоставляя и сравнивая числа, учащиеся устанавливают, что для запи­си числа, состоящего из единиц, требуется одна цифра (один знак); для записи числа, состоящего из десятков или десятков и единиц, требуется две цифры (два знака). Вводятся термины «однозначные» и «двузначные» числа. Дети приводят примеры однозначных и двузначных чисел, выполняют упражнения на различение однозначных и двузначных чисел, например: «Выпи­шите из ряда чисел сначала однозначные, а потом двузначные числа: 2, 13, 8, 17» 15, 6, 11, 10; запишите 4 любых однознач­ных числа и увеличьте каждое на 10. Какие числа у вас полу­чились, как можно их назвать?

---

С целью систематизации знаний по нумерации полезно в конце работы над темой включать задания по характеристике заданных чисел. Характеризуя, например, число 13, учащиеся могут назвать его десятичный со­став (в этом числе 1 дес. и 3 ед., или 1 ед. II разряда и 3 ед. I разряда), сказать о месте это­го числа в натуральной последовательности (число 13 называют при счете после 12 и перед 14). Также полезно проводить задания на сравнение этих чисел с рисунками, изображенные на которых предметы соответствуют этому числу.

В результате изучения темы «Сложение и вычитание» уча­щиеся должны научиться осознанно выполнять сложение и вы­читание любых чисел в пределах 100, твердо усвоить табличные случаи сложения и вычитания с переходом через десяток, а так­же ряд теоретических вопросов.

Как и при изучении первого десятка, приемы сложения и вычитания в пределах 20 раскрываются в органической связи с изучением теоретического материала. При таком подходе лучше усваиваются вопросы теории, так как они находят при­менение, и быстрее формируются более осознанные вычислительные навыки.

Анализ приемов сложения и вычитания чисел в пределах 20 показывает, что для их осознанного выполнения учащиеся дол­жны хорошо знать нумерацию чисел в пределах 20, твердо знать таблицу сложения и соответствующие случаи вычитания в пределах 10 и, кроме того, усвоить следующие свойства дей­ствий сложения и вычитания: прибавление числа к сумме, вычи­тание числа из суммы, прибавление суммы к числу, вычитание суммы из числа, прибавление суммы к сумме и вычитание сум­мы из суммы.

Сложение и вычитание рассматриваются в таком порядке.

Рассмотрим подробнее методику изучения свойств и вычи­слительных приемов.

На двух-трех уроках, ученики проговаривают объяснение вслух, а затем про себя. В резуль­тате упражнений у учащихся постепенно вырабатывается навык.

Введению свойства прибавления числа к сумме должна предшествовать специальная подготовительная работа, в результате которой учащиеся знакомятся с мате­матическими выражениями «сумма чисел...» и «разность чисел...», учатся читать и записывать выражения со скобками, за­менять двузначные неразрядные числа суммой их разрядных слагаемых. Эти вопросы рассматриваются при изучении сложе­ния и вычитания чисел в пределах 10 и нумерации чисел в пре­делах 20.

Изучение каждого свойства строится примерно по одному плану: сначала, используя наглядные пособия, надо раскрыть суть самого свойства, затем научить детей применять его при выполнении различных упражнений учебного характе­ра, и, наконец, научить, пользуясь знанием свойства, находить рациональные приемы вычислений с учетом особенностей каж­дого конкретного случая.

---

Рассмотрим, как можно провести ознакомление детей со свойством прибавления числа к сумме.

Раскрывая суть свойства, надо показать детям, что число к сумме можно прибавлять различными способами: можно вычис­лить сумму и к полученному результату прибавить число, можно прибавить число к первому слагаемому и к полученному резуль­тату прибавить второе слагаемое, а можно прибавить число ко второму слагаемому и полученный результат сложить с первым слагаемым. Везде при этом у первоклассников формируется операции сравнения нового числа с другим, ранее изученным.

Покажем, как это можно сделать.

Учитель. Пишет на доске выражение (5+3)+2. Прочитайте пример. (К сумме чисел 5 и 3 прибавить 2.) Назовите сумму. (5 плюс 3.) Назовите первое слагаемое этой суммы. (5.) Назовите второе слагаемое. (3.) Назовите число, которое надо прибавить к этой сумме. (2.) Как найти резуль­тат? (Вычислю сумму, получится 8; прибавлю 2, получится 10.)



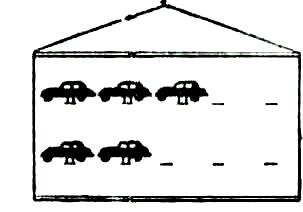
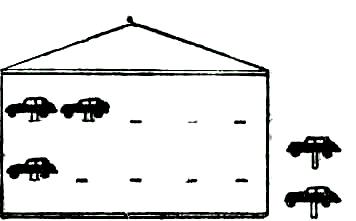
рис.3.

На доске запись: (5+3)+2=8+2=10.

Сегодня вы научитесь прибавлять число к сумме и другими способами.

Учитель. (Вывешивает на доске рисунки двух гаражей и пред­лагает ученикам приготовить прямоугольники голубого, зеле­ного и красного цветов, вырезанные из бумаги). Это гаражи. Число машин в первом гараже будет изобра­жать первое слагаемое. Сколько машин надо поставить в пер­вый гараж? (5.)

Учитель. (Вставляет в прорези 5 машин голубого цвета, выре­занные из картона, а учащиеся раскладывают на партах 5 го­лубых прямоугольников). Число машин во втором гараже будет изображать второе слагаемое. Сколько машин поставим во второй гараж? (3.)

Учитель (ставит во второй гараж 3 зеленые машины, а де­ти раскладывают на партах 3 зеленых прямоугольника). Приехали еще две машины (прикрепляют к доске две крас­ные машины, а учащиеся кладут на парту два красных прямо­угольника).

На доске располагаются рисунки (рис. 1).

Учитель. Красные машины надо поставить в гараж. В какой гараж их можно поставить? (В первый или во второй), доставим их в первый гараж. (Учитель «ставит» машины в первый гараж, а дети придвигают красные прямоугольники к голубым). Как теперь узнаем, сколько всего машин?

Дети. К 5 прибавить 2, полу­чится 7, и еще прибавить 3, получится 10.

Учитель. Да, число 2 мы при­бавили к 5, первому слагаемому, потом к полученному резуль­тату, к 7, прибавили второе слагаемое 3. Сравните ответы.

---