ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 249
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
деп белгілейді. Вектордың координаталары  ={x,y,z} немесе
={x,y,z} немесе
 =xi+yj+zk.
=xi+yj+zk.
Егер А (х1,у1,z1) және В (х2,у2,z2) нүктелері берілсе, онда АВ векторының координаталары оның ұшы В координаталарынан бас нүктеі А-ның сәйкес координаталарын алу арқылы анықталады: ={x2-x1,y2-y1,z2-z1}. Вектордың ұзындығы |
={x2-x1,y2-y1,z2-z1}. Вектордың ұзындығы | | немесе
| немесе 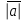 деп белгіленеді және вектордың модулі деп аталады.
деп белгіленеді және вектордың модулі деп аталады.
| |=
|=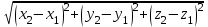
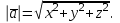
Басы мен ұшы беттесіп келетін вектор нөлдік вектор деп аталады. Ұзындығы бірге тең вектор бірлік вектор деп аталады. Бір немесе параллель түзуде жататын векторлар коллинеар векторлар деп аталады.
 =(x1,y1,z1) және
=(x1,y1,z1) және  =(x2,y2,z2) векторларының коллинеар болу шарты:
=(x2,y2,z2) векторларының коллинеар болу шарты:
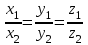
Бір немесе параллель жазықтықта жатса, онда ол векторлар компланар векторлар деп аталады.Егер мен
мен  векторлары бірдей бағытталған және модульдары бірдей болса, онда олар тең векторлар деп аталады.
векторлары бірдей бағытталған және модульдары бірдей болса, онда олар тең векторлар деп аталады.
Векторларды қосу үшін үшбұрыш немесе параллелограмм әдістері қолданылады.
 ={xa,ya,za},
={xa,ya,za},  ={xв,yв,zв} векторлары берілсін. Онда
={xв,yв,zв} векторлары берілсін. Онда
Берілген а векторының OX,OУ,OZ осьтерімен жасайтын бұрыштарын α, β, γ деп белгілейік. Бұл бұрыштар вектордың бағытын анықтайды.Вектордың бағыттауыш косинустары:
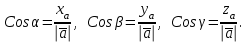
Бағыттауыш косинустары арасындағы байланыс
cos2α + cos2β+ cos2γ=1.
 векторының ОХ осіне проекциясы осы вектордың модулін вектор мен осьтің арасындағы бұрыштың косинусына көбейткенге тең
векторының ОХ осіне проекциясы осы вектордың модулін вектор мен осьтің арасындағы бұрыштың косинусына көбейткенге тең
прох =|
=| |cosφ.
|cosφ.
Екі вектордың скаляр көбейтіндісі деп осы векторлардың ұзындықтары мен олардың арасындағы бұрыштың косинусының көбейтіндісіне тең болатын санды айтады және ·
·  немесе (
немесе (
 ) деп белгіленеді. Анықтама бойынша
) деп белгіленеді. Анықтама бойынша  ·
·  =|
=| | |
| | | cosφ.
| cosφ.
Егер және
және  векторлары перпендикуляр болса, онда олардың скалярлық көбейтіндісі нөлге тең
векторлары перпендикуляр болса, онда олардың скалярлық көбейтіндісі нөлге тең
 ·
·  =0
=0
Егер ={xa,ya,za} және
={xa,ya,za} және ={xв,yв,zв} векторлары берілсе, онда олардың скалярлық көбейтіндісі
={xв,yв,zв} векторлары берілсе, онда олардың скалярлық көбейтіндісі
 ·
·  =xa xb+ya yb+za zb
=xa xb+ya yb+za zb
Егер екі вектор арасындағы бұрышты φ деп белгілесек, онда
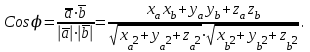
 мен
мен  векторларының векторлық көбейтіндісі деп келесі түрде анықталған
векторларының векторлық көбейтіндісі деп келесі түрде анықталған  векторын айтамыз.
векторын айтамыз.
1. =
= 
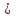
 вектордың ұзындығы |
вектордың ұзындығы |
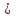
 |=|
|=| |
|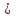 |
| | sin φ=|
| sin φ=| |. а мен в векторларынан салынған параллелограмм ауданына тең.
|. а мен в векторларынан салынған параллелограмм ауданына тең.
2. =
= 
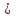

→

 ,
, 

 , яғни
, яғни  мен
мен  векторлар жазықтығына перпендикуляр
векторлар жазықтығына перпендикуляр
3. [

 ] векторлары ұшынан қарағанда
] векторлары ұшынан қарағанда  дан
дан  -ға бұрылу бағыты сағат тіліне қарсы болуы керек.
-ға бұрылу бағыты сағат тіліне қарсы болуы керек.
Егер және
және  векторлары координаталары арқылы берілсе, яғни
векторлары координаталары арқылы берілсе, яғни
 =
= 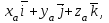
 =
= 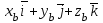
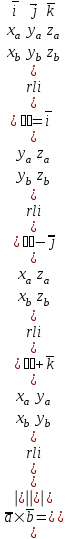

Үш ,
, ,
, векторлардың аралас көбейтіндісі деп
векторлардың аралас көбейтіндісі деп  және
және  векторлық көбейтіндісін
векторлық көбейтіндісін  векторымен скаляр көбейткендегі санды айтады. Векторларды аралас көбейту (
векторымен скаляр көбейткендегі санды айтады. Векторларды аралас көбейту (

 ) ·
) · немесе
немесе
1) Vпарал/пед= ·
·  ·
· Vпр/да=
Vпр/да=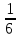 |
| ·
·  ·
· |
|
2) Көбейткіштерді айнала ауыстырудан аралас көбейтіндінің шамасы өзгермейді.


 ·
· =
=

 ={x,y,z} немесе
={x,y,z} немесе  =xi+yj+zk.
=xi+yj+zk.Егер А (х1,у1,z1) және В (х2,у2,z2) нүктелері берілсе, онда АВ векторының координаталары оның ұшы В координаталарынан бас нүктеі А-ның сәйкес координаталарын алу арқылы анықталады:
 ={x2-x1,y2-y1,z2-z1}. Вектордың ұзындығы |
={x2-x1,y2-y1,z2-z1}. Вектордың ұзындығы | | немесе
| немесе 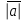 деп белгіленеді және вектордың модулі деп аталады.
деп белгіленеді және вектордың модулі деп аталады.|
 |=
|=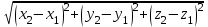
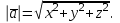
Басы мен ұшы беттесіп келетін вектор нөлдік вектор деп аталады. Ұзындығы бірге тең вектор бірлік вектор деп аталады. Бір немесе параллель түзуде жататын векторлар коллинеар векторлар деп аталады.
 =(x1,y1,z1) және
=(x1,y1,z1) және  =(x2,y2,z2) векторларының коллинеар болу шарты:
=(x2,y2,z2) векторларының коллинеар болу шарты: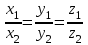
Бір немесе параллель жазықтықта жатса, онда ол векторлар компланар векторлар деп аталады.Егер
 мен
мен  векторлары бірдей бағытталған және модульдары бірдей болса, онда олар тең векторлар деп аталады.
векторлары бірдей бағытталған және модульдары бірдей болса, онда олар тең векторлар деп аталады.Векторларды қосу үшін үшбұрыш немесе параллелограмм әдістері қолданылады.
 ={xa,ya,za},
={xa,ya,za},  ={xв,yв,zв} векторлары берілсін. Онда
={xв,yв,zв} векторлары берілсін. Онда-
 +
+ =
=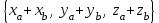
-
 -
- =
= 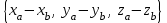
-
R =
= 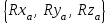
Берілген а векторының OX,OУ,OZ осьтерімен жасайтын бұрыштарын α, β, γ деп белгілейік. Бұл бұрыштар вектордың бағытын анықтайды.Вектордың бағыттауыш косинустары:
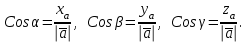
Бағыттауыш косинустары арасындағы байланыс
cos2α + cos2β+ cos2γ=1.
 векторының ОХ осіне проекциясы осы вектордың модулін вектор мен осьтің арасындағы бұрыштың косинусына көбейткенге тең
векторының ОХ осіне проекциясы осы вектордың модулін вектор мен осьтің арасындағы бұрыштың косинусына көбейткенге тең прох
 =|
=| |cosφ.
|cosφ.Екі вектордың скаляр көбейтіндісі деп осы векторлардың ұзындықтары мен олардың арасындағы бұрыштың косинусының көбейтіндісіне тең болатын санды айтады және
 ·
·  немесе (
немесе (
 ) деп белгіленеді. Анықтама бойынша
) деп белгіленеді. Анықтама бойынша  ·
·  =|
=| | |
| | | cosφ.
| cosφ. -
 ·
·  =
= ·
·
-
 ·
·  =|
=| |·пр
|·пр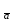
 =|
=| | пр
| пр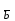

-
( +
+ )·
)·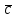 =
= ·
·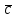 +
+ ·
·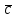
-
(λ
 )=λ(
)=λ( ·
·  )
)
Егер
 және
және  векторлары перпендикуляр болса, онда олардың скалярлық көбейтіндісі нөлге тең
векторлары перпендикуляр болса, онда олардың скалярлық көбейтіндісі нөлге тең  ·
·  =0
=0Егер
 ={xa,ya,za} және
={xa,ya,za} және ={xв,yв,zв} векторлары берілсе, онда олардың скалярлық көбейтіндісі
={xв,yв,zв} векторлары берілсе, онда олардың скалярлық көбейтіндісі  ·
·  =xa xb+ya yb+za zb
=xa xb+ya yb+za zbЕгер екі вектор арасындағы бұрышты φ деп белгілесек, онда
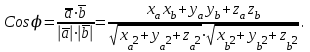
 мен
мен  векторларының векторлық көбейтіндісі деп келесі түрде анықталған
векторларының векторлық көбейтіндісі деп келесі түрде анықталған  векторын айтамыз.
векторын айтамыз.1.
 =
= 
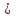
 вектордың ұзындығы |
вектордың ұзындығы |
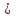
 |=|
|=| |
|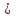 |
| | sin φ=|
| sin φ=| |. а мен в векторларынан салынған параллелограмм ауданына тең.
|. а мен в векторларынан салынған параллелограмм ауданына тең.2.
 =
= 
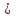

→


 ,
, 

 , яғни
, яғни  мен
мен  векторлар жазықтығына перпендикуляр
векторлар жазықтығына перпендикуляр3. [


 ] векторлары ұшынан қарағанда
] векторлары ұшынан қарағанда  дан
дан  -ға бұрылу бағыты сағат тіліне қарсы болуы керек.
-ға бұрылу бағыты сағат тіліне қарсы болуы керек.-
Егер және
және  коллинеарлы болса, онда
коллинеарлы болса, онда 

 =0
=0 -


 =-
=-


-
(λ )
)
 = λ
= λ


-
( +
+ )
)
 =
=

 +
+


Егер
 және
және  векторлары координаталары арқылы берілсе, яғни
векторлары координаталары арқылы берілсе, яғни  =
= 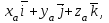
 =
= 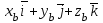
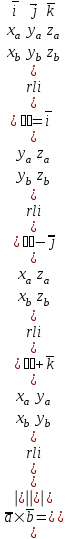

Үш
 ,
, ,
, векторлардың аралас көбейтіндісі деп
векторлардың аралас көбейтіндісі деп  және
және  векторлық көбейтіндісін
векторлық көбейтіндісін  векторымен скаляр көбейткендегі санды айтады. Векторларды аралас көбейту (
векторымен скаляр көбейткендегі санды айтады. Векторларды аралас көбейту (

 ) ·
) · немесе
немесе 1) Vпарал/пед=
 ·
·  ·
· Vпр/да=
Vпр/да=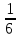 |
| ·
·  ·
· |
|2) Көбейткіштерді айнала ауыстырудан аралас көбейтіндінің шамасы өзгермейді.


 ·
· =
=
