· = ·
3) Кез келген екі көбейткішті ауыстырып қоюдан аралас көбейтіндінің таңбасы кері өзгереді.

=-

4) Егер көбейткіш векторлар компланарлы болса, онда аралас көбейтінді нөлге тең:

· =0

Егер , , векторлары координаталары арқылы берілсе, ={x_a,y_a,z_a}, ={x_в,y_в,z_в}, = {x_c, y_c, z_c}, онда осы векторлардың аралас көбейтіндісі келесі формуламен анықталады · 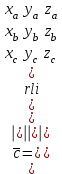. , , векторларының компланарлы болу шарты

---

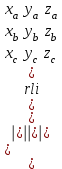=0.

Ұсынылатын әдебиеттер

1.Дүйсек А.К., Қасымбеков С.Қ. Жоғары математика. Алматы, 2004.

2.Ефимов Н.В. Краткий курс аналитической геометрии. М.: Наука, 1969.

3.Письменный Д. Конспект лекций по высшей математики. ч. 1., М.: Айрис пресс, 2004.

4.Лунгу К.Н. Сборник задач по высшей математики. 1 курс. М.: Айрис пресс, 2005.

СӨЖ-ге арналған бақылау тапсырмалары

ЖҮТ 2.1; ЖҮТ 2.2; [10, том 1, беттер 69-85]

Есептер: АЗ-2.1; АЗ-2.2; АЗ-2.3; [10, том 1]

---

III бөлім. Жазықтықтағы және кеңістіктегі аналитикалық геометрия

4-тақырып. Жазықтықтағы түзу теңдеулері. Екінші ретті қисықтар

Лекция жоспары:

1. 
   Жазықтықтағы координаталар жүйелері. Жазықтықтағы аналитикалық геометрияның қарапайым есептері.
   
2. 
   Түзудің әртүрлі теңдеулері. Түзудің қалыпты теңдеуі, екінші ретті қисықтар: эллипс, гипербола, парабола және олардың канондық теңдеулері.
   
3. 
   Декарт координаттарын түрлендіру. Екінші ретті сызықтарды канондық түрге келтірудің ең қарапайым есептері. Шеңбер теңдеуі, Эллипс, гипербола жане парабола теңдеулері
   

Лекцияның қысқаша жазбасы

Жазықтықтағы координаталар жүйесі – жазықтықтағы нүктені сандық тұрғыдан суреттеу ұғымын білдіреді. Мұндай жүйелердің бірі тікбұрышты координаталар жүйесі болады. 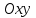координаталар жүйесіндегі 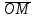радиус-векторының координаталары М нүктесінің координатасы деп атайды. Егер 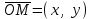болса, онда М нүктесінің координаталары 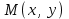деп жазылады. Мұнда х-саны М нүктесінің абсцисса, ал у-саны М нүктесінің ординатасы болады.

Бұл екі х және у сандары М нүктесінің жазықтықтағы орналасуын анықтайды. х және у –тің әрбір қос сан сандар мәніне бір ғана М нүктесі сәйкес келеді.

Координаталар жүйесінде аса маңызды орын алатын жүйе полярлық координаталар жүйесі.

Координаталар жүйесін түрлендіру. Бір координаталар жүйесінен басқа координаталар жүйесіне ауысуын координаталар жүйесін түрлендіру деп атайды.

Тікбұрышты координаталар жүйесінің басқа координаталар жүйесіне ауысуын екі жағдайын қарастырайық.

Алынған формулалар әр түрлі координаталар жүйесінде жазықтықтан алынған кез-келген нүктенің координаталарының тәуелділігін анықтайды.

Координаталар осьтерін параллель көшіру. Жазықтықта 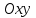тікбұрышты координаталар жүйесі берілсін. 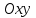координаталары жүйесінің жаңа 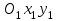координаталар жүйесіне параллель көшіруде координаталар басы өзгеріп, масштаб бірліктері мен ось бағыттары өзгермейді.

---

Жазықтықтағы түзудің теңдеулері. Сызықтардың ішінде ең қарапайымы ол – түзу. Тікбұрышты координаталар жүйесінде

Бұрыштың коэффициентпен берілген түзудің теңдеуі Түзу бойынан кез-келген 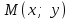нүктесін аламыз

,

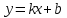теңдеуін аламыз, ол кез-келген 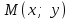нүктесінің координаталарын қанағаттандырады. 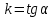саны түзудің бұрыштық коэффициенті, ал (10.2) теңдеуі – бұрыштық коэффициенті, ал (10.2) теңдеуі бұрыштық коэффициентімен берілген түзудің теңдеуі деп аталады. Түзудің жалпы теңдеуі. 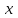пен 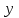-ке қатысты бірінші дәрежелі түзудің теңдеуін қарастырайық.

,

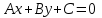мұндағы 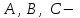тұрақты шамалар, 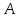және 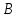бірдей нөлге тең болмайды. Берілген бағытпен берілген нүктеден өтетін түзудің теңдеуі.

Түзу 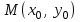нүктесі арқылы өтетіндіктен, нүктенің координаталары түзудің теңдеуін қанағаттандырады: 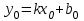. Бұл теңдеуде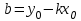н . мәнін 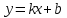теңдеуіне апарып қойсақ, онда іздеп отырған 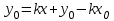теңдеуін аламыз, яғни

.

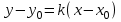Екі нүкте арқылы өтетін түзудің теңдеуі. Түзу

---

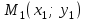және 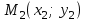нүктелері арқылы өтеді. 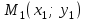нүктесі арқылы өтетін түзудің теңдеуі

.

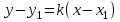мұндағы 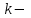әзірше белгісіз коэффициент.

Түзудің нормаль теңдеуі. Түзу р және 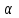арқылы анықталатын болсын. 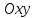тікбұрышты координаталар жүйесін қарастырайық. Бірақ тікбұрышты және полярлық координаталар жүйесін байланыстыратын 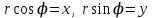формулалары белгілі.

.

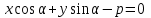теңдеуі түзудің нормаль теңдеуі деп аталады.

Шеңбер. Екінші ретті қисықтардың ішіндегі ең қарапайым қисық – шеңбер. Радиусы 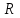, центрі 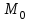нүктесінде болатын шеңбер деп 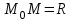шартын қанағаттандыратын, жазықтықтың барлық 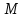нүктелер жиынын айтатынын еске салайық. Тікбұрышты координаталар жүйесінде 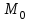нүктесінің координаталары 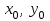болсын, ал 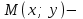шеңбердің бойынан алынған кез-келген нүкте 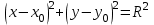теңдеуі шеңбердің канондық теңдеуі деп аталады.

Эллипс. Фокустар деп аталатын берілген екі нүктеден қашықтарының қосындысы әрқашан тұрақты шама болатын нүктелердің геометриялық орындарын эллипс деп аталады .

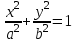Гипербола. Фокустар деп аталатын берілген екі нүктеден қашықтықтарының айырымы әрқашанда тұрақты шама болатын нүктелерінің геометриялық орындарын гипербола деп аталады

---

Смотрите также файлы

• Расчет режимов электроконтактной сварки вводная часть.docx

• Заымдану, сыну, жаралану, буыны шыусоып алу, кйік, су кезіндегі алашы кмек.docx

• Если у человека есть заранее сформированная предрасположенность реагировать на чтото определённым образом, то и делать это он будет в соответствии с ней.docx

• Стихи о родине.docx

• Лабораторная работа 1 Изучение устройства и работы сцеплений и их приводов по курсу Конструкция автомобилей 1 Тема Трансмиссия Цели и задачи работы изучить устройство и работу сцеплений и их приводов.docx