ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 252
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
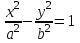
Парабола. Фокус деп аталатын берілген нүктеден және директриса деп аталатын берілген түзуден арақашықтықтары бірдей болатын нүктелердің жиынтығын парабола деп атайды.
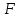 фокусынан директрисаға дейінгі қашықтық параметр деп аталады және
фокусынан директрисаға дейінгі қашықтық параметр деп аталады және 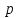 әрпімен белгіленеді. (
әрпімен белгіленеді. (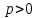 ).
).Параболаның теңдеуін қорытып шығару үшін
 координаталар жүйесін алайық. Ал координаталар басы фокус пен директрисаның дәл ортасына орналастырып, директрисадан
координаталар жүйесін алайық. Ал координаталар басы фокус пен директрисаның дәл ортасына орналастырып, директрисадан 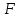 фокусына қарай бағытталған, директрисаға перпендикуляр
фокусына қарай бағытталған, директрисаға перпендикуляр 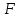 фокусы арқылы өтетін
фокусы арқылы өтетін 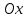 осін алайық. Қарастырып отырған жүйеде
осін алайық. Қарастырып отырған жүйеде 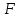 фокусының координаталары
фокусының координаталары 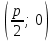 , ал директриса теңдеуі
, ал директриса теңдеуі 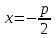 немесе
немесе 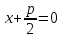 түрінде беріледі.
түрінде беріледі. 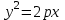 теңдеуі параболаның канондық теңдеуі деп аталады. Парабола екінші ретті сызық болып табылады.
теңдеуі параболаның канондық теңдеуі деп аталады. Парабола екінші ретті сызық болып табылады. Ұсынылатын әдебиеттер
1.Дүйсек А.К., Қасымбеков С.Қ. Жоғары математика. Алматы, 2004.
2.Ефимов Н.В. Краткий курс аналитической геометрии. М.: Наука, 1969.
3.Письменный Д. Конспект лекций по высшей математики. ч. 1., М.: Айрис пресс, 2004.
4.Лунгу К.Н. Сборник задач по высшей математики. 1 курс. М.: Айрис пресс, 2005.
СӨЖ-ге арналған бақылау тапсырмалары
ЖҮТ 3.2; [10, том 1, беттер 69-85]
Есептер АЗ-3.3; [10, том 1]
ЖҮТ 4.1; [10, том 1, беттер 137-142]
Есептер АЗ-4.1; [10, том 1]
5-тақырып. Кеңістіктегі жазықтықтың және түзудің теңдеулері. Екінші ретті беттер
Лекция жоспары:
-
Кеңістіктегі жазықтық теңдеулері -
Кеңістіктегі түзу теңдеулері -
Екінші ретті беттер.
Лекцияның қысқаша мазмұны:
Кеңістіктегі жазықтық теңдеуі
Қарапайым беттердің бір түрі жазықтық.
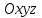 кеңістіктегі жазықтықты әр түрлі түрде беруге болады. Олардың әрқайсысына сәйкес теңдеулері болады.
кеңістіктегі жазықтықты әр түрлі түрде беруге болады. Олардың әрқайсысына сәйкес теңдеулері болады.Берілген нүкте арқылы өтетін, берілген векторға перпендикуляр жазықтықтың теңдеуі.
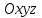 кеңістігінде
кеңістігінде 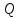 жазықтығы
жазықтығы 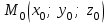 нүктесімен және осы жазықтыққа перпендикуляр
нүктесімен және осы жазықтыққа перпендикуляр 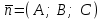 векторымен берілген.
векторымен берілген. 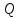 жазықтығының теңдеуін қорытып шығарайық. Жазықтықтан кез-келген
жазықтығының теңдеуін қорытып шығарайық. Жазықтықтан кез-келген 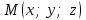 нүктесін алайық және
нүктесін алайық және 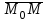 векторын құрайық.
векторын құрайық. 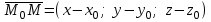
М нүктесі
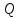 жазықтығында қалай орналассада
жазықтығында қалай орналассада 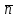 және
және 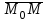 векторлары өзара перпендикуляр болады, сондықтан олардың скаляр көбейтіндісі нөлге тең:
векторлары өзара перпендикуляр болады, сондықтан олардың скаляр көбейтіндісі нөлге тең: 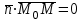 , яғни
, яғни | | 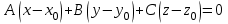 . . | |
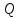 жазықтығының кез-келген нүктесі теңдеуін қанағаттандырады, ал
жазықтығының кез-келген нүктесі теңдеуін қанағаттандырады, ал 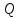 жазықтығында жатпайтын нүктелер қанағаттандырмайды.
жазықтығында жатпайтын нүктелер қанағаттандырмайды.  ,
,  , және
, және 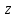 координаталарына байланысты жазықтықтың теңдеуі бірінші дәрежелі болады.
координаталарына байланысты жазықтықтың теңдеуі бірінші дәрежелі болады. 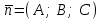
векторы жазықтықтың нормаль векторы деп аталады. Теңдеудегі
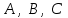 коэффициенттеріне мәндер беріп,
коэффициенттеріне мәндер беріп,  нүктесі арқылы өтетін кез-келген жазықтықтың теңдеуін алуға болады. Берілген нүкте арқылы өтетін жазықтықтар жиынын жазықтықтар байланысы деп, ал (12.3) –жазықтықтар байланысының теңдеуі деп аталады.
нүктесі арқылы өтетін кез-келген жазықтықтың теңдеуін алуға болады. Берілген нүкте арқылы өтетін жазықтықтар жиынын жазықтықтар байланысы деп, ал (12.3) –жазықтықтар байланысының теңдеуі деп аталады. Жазықтықтың жалпы теңдеуі
 ,
,  , және
, және  үш белгісізді бірінші дәрежелі теңдеуді қарастырайық:
үш белгісізді бірінші дәрежелі теңдеуді қарастырайық:| | 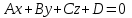 . . | |
Осы теңдеуді
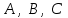 коэффициенттерінің бірдей нөлге тең емес болсын, мысалы,
коэффициенттерінің бірдей нөлге тең емес болсын, мысалы, 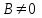 , онда (12.4) теңдеуін былайша жазуға болады:
, онда (12.4) теңдеуін былайша жазуға болады:| | 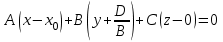 . . | |
теңдеуі
 координаталар жүйесіндегі қандай да бір жазықтықты анықтайды. теңдеуі жазықтықтың жалпы теңдеуі деп аталады.
координаталар жүйесіндегі қандай да бір жазықтықты анықтайды. теңдеуі жазықтықтың жалпы теңдеуі деп аталады. Берілген үш нүкте арқылы өтетін жазықтықтың теңдеуі
Кеңістікте бір түзудің бойында жататын үш нүкте бір ғана жазықтықты анықтайды. Бір түзуде жатпайтын
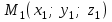 ,
, 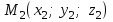 және
және 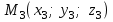 нүктелері арқылы өтетін
нүктелері арқылы өтетін  жазықтығының теңдеуін табайық.
жазықтығының теңдеуін табайық.Жазықтықтан қалауымызша кез-келген
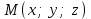 нүктесін алайық және
нүктесін алайық және 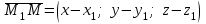 ,
, 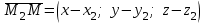 ,
,  векторларын құрайық. Бұл векторлар
векторларын құрайық. Бұл векторлар 
жазықтығында жатады, олар компланарлы векторлар. Векторлардың компланар шартын қолданып (олардың аралас көбейтіндісі нөлге тең),
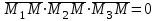 , аламыз, яғни
, аламыз, яғни | | 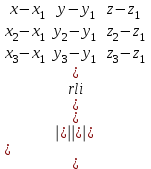 . . | |
теңдеуі берілген үш нүкте арқылы өтетін жазықтықтың теңдеуі.
Жазықтықтың кесінділер арқылы берілген теңдеуі
Жазықтық
 ,
, 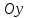 және
және 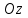 осьтерін
осьтерін  ,
,  және
және 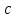 кесінділерін қияды, яғни ол
кесінділерін қияды, яғни ол 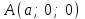 ,
, 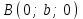
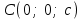 нүктелері арқылы өтеді.
нүктелері арқылы өтеді. Осы нүктелердің координаталарын (12.6) теңдеуіне қойып, келесі анықтауышты аламыз
| | 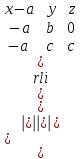 . . | |
Анықтауышты ашып
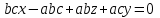 аламыз, яғни
аламыз, яғни 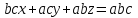 немесе
немесе | | 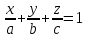 . . | |
теңдеуі координаталар осьтеріндегі жазықтық кесінділер бойынша теңдеуі деп аталады. Бұл теңдеу жазықтықтарды салғанда қолданған ыңғайлы.
Жазықтықтың нормаль теңдеуі
ОК=р болсын, болсын онда
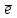 бірлік векторының
бірлік векторының 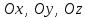 остерімен жасайтын бұрыштары
остерімен жасайтын бұрыштары 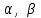 және
және 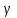 болады. Онда
болады. Онда 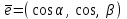
жазықтықпен кез-келген
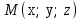 нүктесін алып, оны координаталар басымен қосайық. Сонда
нүктесін алып, оны координаталар басымен қосайық. Сонда 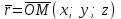 векторын аламыз:
векторын аламыз:| | 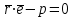 , , | |
(12.8) –теңдеуі векторлық формадағы жазықтықтың нормаль теңдеуі деп аталады.
 және
және  векторларының координаталары белгісіз,
векторларының координаталары белгісіз, | | 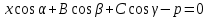 , , | |
теңдеуі координаталық формадағы жазықтықтың нормаль теңдеуі.
Кеңістіктегі түзудің теңдеулері. Түзудің векторлық теңдеуі
Кеңістіктегі түзудің теңдеуі. Түзудің кез-келген
 нүктесі және осы
нүктесі және осы түзуге параллель
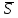 векторымен анықталады.
векторымен анықталады. 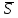 векторы түзудің бағыттауыш векторы деп аталады.
векторы түзудің бағыттауыш векторы деп аталады. 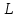 түзуі өзінің
түзуі өзінің 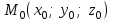 нүктесімен және
нүктесімен және 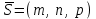 бағыттауыш векторымен берілсін. Түзудің бойынан кез-келген
бағыттауыш векторымен берілсін. Түзудің бойынан кез-келген  нүктесін белгілеп алайық.
нүктесін белгілеп алайық.  және
және  нүктелерінің радиус векторларын
нүктелерінің радиус векторларын 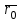 және
және  арқылы белгілейік.
арқылы белгілейік. 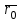 ,
,  ,
,  үш векторы
үш векторы| | 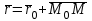 . . | |