қатынасымен байланысты.

түзуінің бойында жатқан векторы бағыттауыш векторына параллель, сондықтан 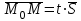, мұндағы 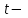параметр деп аталатын скалярлық көбейткіш, ол түзудің М нүктесінен тәуелді әр түрлі мәндер қабылдайды.формуласын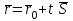

түрінде жазуға болады. Бұл шыққан теңдеуді түзудің векторлық теңдеуі деп аталады.

Түзудің параметрлік теңдеуі

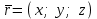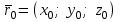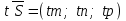, , ескере отырып

.

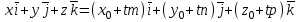түрінде жазуға болады.

Бұдан

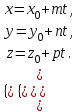теңдігі шығады. Бұл теңдеуді түзудің параметрлік теңдеуі деп атайды.

Түзудің канондық теңдеуі

векторы түзуінің бағытауыш векторы, ал нүктесі осы түзуде жататын нүктесі. түзуінің бойындағы нүктесін нүктесімен қосып, векторына параллель векторын жүргіземіз. Сондықтан, және

---

пропорционал болады:

.

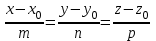теңдеуі түзудің канондық теңдеуі деп аталады.

Екі нүкте арқылы өтетін кеңістіктегі түзудің теңдеуі

және нүктелері арқылы өтетін түзуі берілсін. Бағыттауыш векторы ретінде 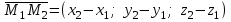векторын алуға болады, яғни 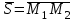(76-суретті қара). Демек, 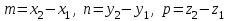. Түзу нүктесі арқылы өтетін болғандықтан, (12.13) теңдеуі бойынша, түзуінің теңдеуі келесі түрде болады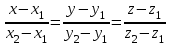

.

теңдеуі берілген екі нүкте арқылы өтетін түзудің теңдеуі деп аталады.

Түзудің жалпы теңдеуі

Кеңістіктегі түзудің теңдеуі параллель емес екі жазықтық қиылсықанда пайда болған сызық арқылы беріледі

,

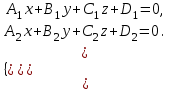теңдеулер жүйесін қарастырайық. Бұл жүйенің әрбір теңдеуі жазықтықты анықтайды. Егер жазықтықтар параллель емес болса ( 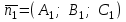және 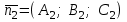) векторларының координаталары пропорционал болмайды.) онда координаталары осы жүйенің әрбір теңдеуін қанағаттандыратын, кеңістіктегі геометриялық орны болатын түзуін анықтайды.

Цилиндрлік беттер

Тұрақты бағытын сақтай отырып және 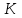қисығын қиятын

---

түзуінің бойымен жылжығанда қозғалысынан пайда болған кеңістікте орналасқан бетті цилиндрлік бет немесе цилиндр деп атайды. қисығын-цилиндрлік бағыттаушысы, ал - цилиндрлік жасаушысы деп атайды Бағыттаушысы координаталар жазықтығының біреуінде, ал жасаушылары координаталар осьтерінде параллель және осы жазықтыққа перпедикуляр орналасқан цилиндрлік бетті қарастырайық.

Теңдеуі 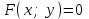болатын, жазықтығында жататын қандай да бір сызығын қарастырайық. Бағыттаушысы болатын және осіне паралллель бағыттауыш бар цилиндрді салайық.

Айналу беттері. Конустық беттер

Егер кеңістікте қандай да бір жазық қисық осьті айналса, оның айналуынан пайда болған бетті айналу беті деп атайды. Қандай да бір қисығы 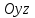жазықтығында жатсын. Бұл қисықтың теңдеуі 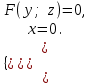түрінде жазылсын.

Берілген Р нүктесі арқылы өтетін және қисық сызығымен қиылсады түзу сызықтармен пайда болған бетті конустық бет немесе конус деп атайды. Мына сызығы – конустың бағыттауышысы, ал Р нүктесі – оның төбесі, ал бетті сипаттайтын түзу жасаушысы деп атайды.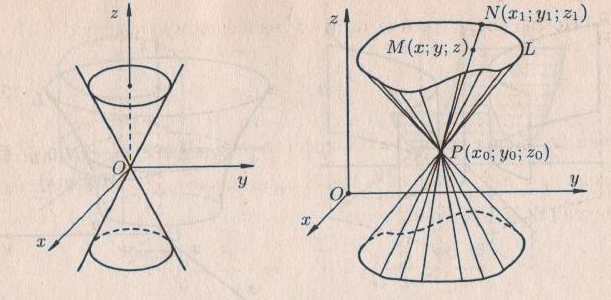



Екінші ретті беттердің конустық теңдеуі

Берілген екінші ретті беттердің теңдеуінен оның геометриялық түрін анықталады. Эллипсоид 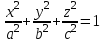теңдеуімен берілген бетті зерттейміз. Бетінің тұйық, сопақ бет болатындығын көрсетеді. (12.28) беті эллипсоид деп аталады. және

---

шамалары эллипсоидтың жарты осьтері деп аталады. Егер олар әртүрлі болса, онда эллипсоид үш осьті деп, ал екі жарты осі тең болса, онда үш осьті эллипсоид айналу эллипсоидына айналады, егер 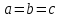, яғни жарты осьтері өзара тең болса, онда ол сфера 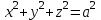деп аталады.

Бір қуысты гиперболоид 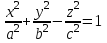. Бұл қиманың сараптамасы 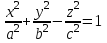теңдеуі мен анықталатын беттің шексіз формасы кеңейтілген түтікше форма тәрізді екенін көрсетеді. 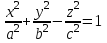бет бірқуысты гиперболоид деп аталады.

Ұсынылатын әдебиеттер

1.Дүйсек А.К., Қасымбеков С.Қ. Жоғары математика. Алматы, 2004.

2.Ефимов Н.В. Краткий курс аналитической геометрии. М.: Наука, 1969.

3.Письменный Д. Конспект лекций по высшей математики. ч. 1., М.: Айрис пресс, 2004.

4.Лунгу К.Н. Сборник задач по высшей математики. 1 курс. М.: Айрис пресс, 2005.

СӨЖ-ге арналған бақылау тапсырмалары

ЖҮТ 3.1; [10, том 1, беттер 69-85]

Есептер АЗ-3.1; АЗ-3.2; [10, том 1]

---

IV бөлім. Талдауға кіріспе
6-тақырып. Сан тізбегі,оның шегі.Функция,оның шегі. Шектер туралы негізгі теоремалар

Лекция жоспары:

1.Жиын ұғымы. Сандық тізбектер. Сандық тізбектердің жинақтылығы. Монотонды шектелген сандық тізбектің шегі. «е» саны. Натурал логарифмдер;

2. Функция. Нүктедегі функцияның шегі. Шексіздіктегі функция шегі. Шектер туралы негізгі теоремалар. Бірінші және екінші тамаша шектер. Шексіз аз және шексіз үлкен функциялар. Шексіз аз функцияларды салыстыру және оларды функцияның шектерін табуда қолдану;

3. Функцияның үздіксіздігі. Үзіліссіз функциялардың негізгі қасиеттері. Негізгі қарапайым функциялардың үздіксіздігі. Функцияның үздікті болатын нүктелерінің классификациясы.
Лекцияның қысқаша жазбасы

1-анықтама. Кез келген ε>0 саны үшін δ= δ (ε) оң саны табылып мына теңсіздікті0<|x-x₀|<δқанағаттандыратын барлық х үшін|f(x)-A|<εтеңсіздігі орындалса, онда А саны х-тің x₀-ге ұмтылғандағы у= f(x) функциясының шегі деп аталады және оны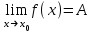 немесе 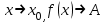символдарымен белгілейді.

2-анықтама. Егер 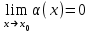болса, онда x₀ нүктесінде 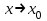ұмтылғанда α=α(x) шексіз аз шама деп аталады.

3-анықтама. Егер 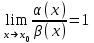болса, онда α(x) және β(х) шексіз аз шамалары х-тің х₀-ге ұмытылғанда эквивалентті шексіз аз шамалар деп аталады және xx₀ұмтылғанда α(x)

β(х) символдарымен белгілейді.

4-анықтама. Егер 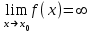болса, онда f (x) функциясы x-x₀-ге ұмытылғанда шексіз үлкен шама деп аталады.Бөлшектің алымы және бөлімі нөлге немесе шексіздікке ұмтылса, онда 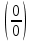немесе 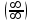анықталмағандықтары деп атайды. Мұндай бөлшектердің шегін анықтау анықталмағандықтарды ашу (айқындау) деп атайды.

---

Смотрите также файлы

• Расчет режимов электроконтактной сварки вводная часть.docx

• Заымдану, сыну, жаралану, буыны шыусоып алу, кйік, су кезіндегі алашы кмек.docx

• Если у человека есть заранее сформированная предрасположенность реагировать на чтото определённым образом, то и делать это он будет в соответствии с ней.docx

• Стихи о родине.docx

• Лабораторная работа 1 Изучение устройства и работы сцеплений и их приводов по курсу Конструкция автомобилей 1 Тема Трансмиссия Цели и задачи работы изучить устройство и работу сцеплений и их приводов.docx