, анықталмағандықтарын ашу үшін келесі теоремалар мен ережелер қолданылады.

1. Теорема.х-тің x₀-ге ұмтылғандағы екі функцияның қатынастарының шегі, х-тің x₀-ге ұмытылғанда функциялардың эквиваленттерінің қатынасының шегіне тең.

α(х) шексіз аз шамасынаң кемімелі дәрежесі бойынша көпмүшесі өзінің соңғы мүшесіне эквивалент болады. α(х) шексіз үлкен шамасының кемімелі дәрежесі бойынша орналасқан көпмүшесі өзінің бірінші мүшесіне эквивалент болады. х 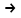х₀ ұмытылғанда рационал бөлшектің алымы және бөлемі 0-ге тең болса, яғни анықталмағандығы шығады. Ол анықталмағандықты ашу үшін бөлшектің алымы мен бөлімін көбейткіштерге жіктеп, онан кейін бөлшекті қысқартып барып шекке көшу керек. Бөлшектің алымы (немесе бөлімі) иррационал болғанда , анықталмағандықтарын ашу үшін алымындағы (немесе бөліміндегі) иррационалдықтан құтылу керек, содан кейін шекке көшу керек.

0·∞, ∞ - ∞, 1^∞ түріндегі анықталмағандықтарды ашу үшін алгебралық түрлендірулер арқылы , анықталмағандықтарына келтіріледі. 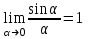шегі бірінші тамаша шек деп аталады.

Шектер туралы негізгі теоремалар

Теорема. Екі функцияның шектерінің қосындысы (айырмасы) олардың шектерінің қосындысына (айырмасына) тең: .

Теорема. Екі функцияның көбейтіндісінің шегі олардың шектерінің көбейтіндісіне тең: .

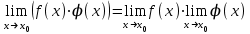Салдар. Тұрақты көбейтіндіні шек таңбасының алдына шығаруға болады

---

.

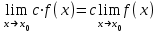
Теорема. Егер бөлшектің бөлімінің шегі 0-ден өзгеше болса, бөлшектің шегі бөлшек алымының шегінің бөлімінің шегіне бөліндісіне тең: .

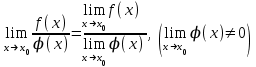Бірінші тамаша шек. Көп жағдайда өрнегі тригонометриялық функциядан құралған шекті есептегенде, бірінші тамаша шек деп аталатын

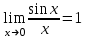шегі қолданылады. Бұл шек былай оқылады: аргументі нөлге ұмтылғандағы синустың аргументіне қатынасының шегі бірге тең.

Екінші тамаша шек

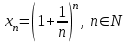сандық тізбегінің шегі е-ге тең (15.6):

.

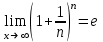Функцияның интервалдағы және кесіндідегі үзіліссіздігі

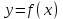функциясы 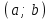интервалында үзіліссіз деп аталады, егер ол осы интервалдың әрбір нүктесінде үзіліссіз болса. 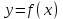функциясы 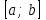интервалында үзіліссіз деп аталады, егер ол 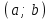интервалында үзіліссіз және 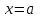нүктесінде оң жақтан, ал 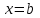нүктесінде сол жақта үзіліссіз болса.

Функцияның үзіліс нүктелері мен олардың жіктелуі

Функция үзіліссіздігі бұзылатын нүктелер функцияның үзіліс нүктелері деп аталады. Егер 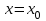нүктесі 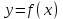функциясының үзіліс нүктесі болса, онда бұл функцияда функция үзіліссіздігінің бірінші анықтамасынан ең болмағанда бір шарты орындалмайды, атап айтқанда:

Функция барлық үзіліс нүктелер бірінші, екінші текті үзіліс нүктелеріне жіктеледі. 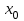нүктесі бірінші текті үзіліс нүктесі деп аталады, егер осы нүктеде функцияның оң, сол нақты ақырлы шектері (бір жақты) бар болса, онда

---

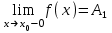және 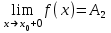. Сонымен қатар,

а) егер 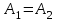болса, онда -қалыпта келтірілетін үзіліс нүктесі, ә) егер 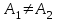болса, онда -ақырлы үзіліс нүктесі деп аталады, егер 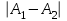шамасын бірінше текті үзіліс нүктесіндегі секіріс деп аталады.

Егер функциясының ең болмағанда біржақты шектерінің (оң және сол жақты) біреуі жоқ болса немесе шексіздікке тең болса, нүктесі функциясының екінші текті үзіліс нүктесі деп аталады.

Үзіліссіз функциялар туралы негізгі теоремалар. Элементар

функциялардың үзіліссіздігі

Теорема. Екі үзіліссіз функцияның қосындысы, көбейтіндісі, бөліндісі үзіліссіз функция (бөлімінің бөлімі 0-ге тең болатын, аргумент мәнінен өзге).

Теорема. 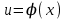функциясы нүктесінде, ал 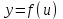функциясы 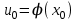нүктесінде үзіліссіз болсын. Сонда үзіліссіз функциядан құралған күрделі 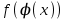функциясы нүктесінде үзіліссіз.
Ұсынылатын әдебиеттер

1.Дүйсек А.К., Қасымбеков С.Қ. Жоғары математика. Алматы, 2004.

2.Ефимов Н.В. Краткий курс аналитической геометрии. М.: Наука, 1969.

3.Письменный Д. Конспект лекций по высшей математики. ч. 1., М.: Айрис пресс, 2004.

4.Лунгу К.Н. Сборник задач по высшей математики. 1 курс. М.: Айрис пресс, 2005.

СӨЖ-ге арналған бақылау тапсырмалары

ЖҮТ 5.1; [10, том 1, беттер 166-176]

Есептер: АЗ-5.1; АЗ-5.2; [10, том 1]

ЖҮТ 5.2; [10, том 1, беттер 178-184]

Есептер: АЗ-5.3; АЗ-5.4; [10, том 1]

IV бөлім.Бір айнымалы функциясын дифференциалдық есептеу(4 сағ.)

---

7-тақырып. Бір айнымалы функцияның дифференциалдық есептеу (2сағ.).

Лекция жоспары:

1. 
   Туынды, туынды ұғымына әкелетін есептер. Туындының геометриялық мағынасы;
   
2. 
   Логарифмдік дифференциалдау, күрделі, дәрежелік және көрсеткіштік функцияларды дифференциалдау формулалары;
   
3. 
   Функцияның дифференциалы, оның туындымен байланысы. Дифференциалдың геометриялық мағынасы. Дифференциалды жуықтап есептеуге қолдану;
   
4. 
   Жоғары ретті дифференциалдар мен туындылар. Маклорен формуласы;
   

Лекцияның қысқаша жазбасы

у=f(x) функциясы х₀нүктесінің қандай да бір маңайында анықталған. Осы функцияның х₀ нүктесіндегі өсімшесі деп 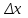айнымалысы функциясын айтады: 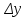=f(x₀+ 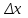)-f(x₀).

Анықтама. Егер 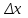нөлге ұмытылғанда функция өсімшесі мен аргумент өсімшесі қатынасының шегі бар болса, онда бұл шек берілген функцияның х₀ нүктесіндегі туындысы деп аталады. Сонымен, егер 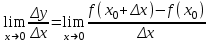бар болса, оны берілген функцияның х₀ нүктесіндегі туындысы деп атайды.

Туындыны мынадай символдармен белгілейді f (x₀), y (x₀) немесе .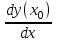

Туындыны табу операциялары дифференциалдау деп аталады.

1. 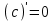2. 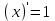3. 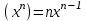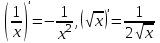4. 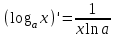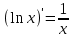5. 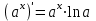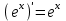6. 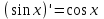7.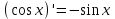

8. 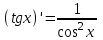9. 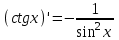10. 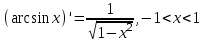11. 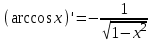12. 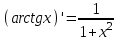13.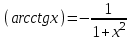

---

Егер u(x) және v(x) функцияларының х₀нүктесінде туындылары бар болса, олардың алгебралық қосындысының, көбейтіндісінің және қатынасының (v(x₀)≠0) x₀ нүктесінде туындылары бар болады және мына формулалар бойынша табылады:



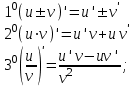
Күрделі функциялардың туындысы:

Егер u=u(x) функцияcының х₀нүктесінде туындысы бар болса: u₀=φ’(х₀) ал у=f(u) функциясының u₀=φ(х₀) нүктесінде туындысы бар болса, онда х₀ нүктесінде y=f(φ(х))=F(x) функциясыныңда туындысы бар болады және мынаған тең 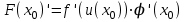немесе .

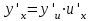Айқындалмаған түрде берілген функция

Егер функция 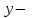ке қатысты шешілген түрінде берілсе, функция айқындалған түрде берілген дейміз.

Айқындалмаған түрде берілген функция деп 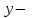ке қатысты шешілмеген, 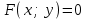түрінде берілген функция түсіндіріледі.

Кез-келген айқындалған функцияны 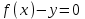теңдеуімен берілген айқындалмаған функция түрінде жаза аламыз, бірақ керісінше жаза алмаймыз. Егер айқындалмаған функция 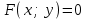түрінде берілсе, 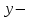тан 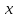бойынша туынды табу үшін теңдеуді 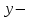ке қатысты шешу қажет емес: ол үшін 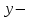ті 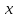-тан тәуелді деп алып, берілген теңдеуді 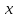бойынша дифференциалдап, алынған теңдеуді

---

Смотрите также файлы

• Расчет режимов электроконтактной сварки вводная часть.docx

• Заымдану, сыну, жаралану, буыны шыусоып алу, кйік, су кезіндегі алашы кмек.docx

• Если у человека есть заранее сформированная предрасположенность реагировать на чтото определённым образом, то и делать это он будет в соответствии с ней.docx

• Стихи о родине.docx

• Лабораторная работа 1 Изучение устройства и работы сцеплений и их приводов по курсу Конструкция автомобилей 1 Тема Трансмиссия Цели и задачи работы изучить устройство и работу сцеплений и их приводов.docx