ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 251
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
қа қатысты шешу жеткілікті.
Параметрлік түрде берілген функция
 аргументі мен
аргументі мен 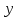 функциясы арасындағы байланыс параметрлік түрде екі теңдеу түрінде берілген болсын:
функциясы арасындағы байланыс параметрлік түрде екі теңдеу түрінде берілген болсын: 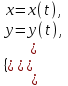 мұндағы
мұндағы  параметр деп аталатын көмекші айнымалы. функциясының туындысы бар деп алып және
параметр деп аталатын көмекші айнымалы. функциясының туындысы бар деп алып және 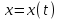 функциясының кері
функциясының кері 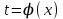 функциясы бар деп алып,
функциясы бар деп алып, 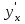 туындысын табайық. Кері функцияны дифференциалдау ережесі бойынша
туындысын табайық. Кері функцияны дифференциалдау ережесі бойынша 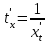 параметрлік түрде берілген
параметрлік түрде берілген  функциясын
функциясын 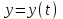 , мұндағы
, мұндағы 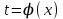 болатын күрделі функция түрінде қарастыруға болады.
болатын күрделі функция түрінде қарастыруға болады.
Туындыны табу үшін бірқатар жағдайларда, алдымен берілген функцияны логарифмдейді. Кейіннен, алынған нәтижені дифференциалдайды. Осылай орындалған амалды – логарифмдік дифференциалдау деп аталады. Туындысы тек логарифмдік дифференциалдау арқылы табылатын функциялар бар. Солардың бірі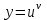 дәреже-көрсеткіштік функциясы, мұндағы
дәреже-көрсеткіштік функциясы, мұндағы 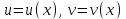 функциялары
функциялары  бойынша дифференциалданатын функциялар. Осы функцияның туындысын табайық:
бойынша дифференциалданатын функциялар. Осы функцияның туындысын табайық:
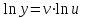 ,
, 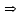
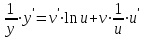 ,
, 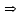
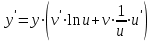 ,яғни
,яғни
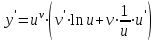 ,
, 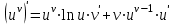 формуласын есте сақтау ережесін тұжырымдайық: дәреже – көрсеткіштік функцияның туындысы
формуласын есте сақтау ережесін тұжырымдайық: дәреже – көрсеткіштік функцияның туындысы 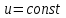
болғандағы көрсеткіштік функцияның туындысы мен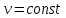 болғандағы дәрежелік функцияның туындысының қосындысына тең.
болғандағы дәрежелік функцияның туындысының қосындысына тең.  функциясының
функциясының 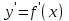 туындысы
туындысы 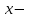 тан тәуелді функция да болып табылады, және бірінші ретті туынды деп аталады. Егер
тан тәуелді функция да болып табылады, және бірінші ретті туынды деп аталады. Егер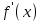 функциясы дифференциал-данатын болса, онда оның туындысы екінші ретті туынды деп аталып,
функциясы дифференциал-данатын болса, онда оның туындысы екінші ретті туынды деп аталып,  арқылы белгіленеді. Сонымен,
арқылы белгіленеді. Сонымен, 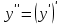 .Екінші ретті туындыдан алынған туынды бар болса, онда ол үшінші ретті туынды деп аталып,
.Екінші ретті туындыдан алынған туынды бар болса, онда ол үшінші ретті туынды деп аталып, 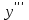 (немесе
(немесе 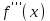 ,
, 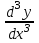 , ...) арқылы белгіленеді. Сонымен,
, ...) арқылы белгіленеді. Сонымен, 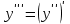 .
. 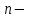 ретті туынды деп
ретті туынды деп 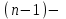 ретті туындыдан алынған туынды аталады:
ретті туындыдан алынған туынды аталады:
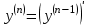 .
.
Анықталмағандықтарды ашу. ,
,  анықталмағандықтарын ашудың тәсілдерінің бірі Лопиталь ережесі болып табылады және ол келесі теоремада негізделген.
анықталмағандықтарын ашудың тәсілдерінің бірі Лопиталь ережесі болып табылады және ол келесі теоремада негізделген.
Теорема:f(x) және φ(х) функциялары х=а нүктесінен басқа х=а нүктесінің маңайындағы нүктелерде дифференциалданатын және анықталған болсын және φ (x)≠0 болсын. Егер х
(x)≠0 болсын. Егер х а ұмтылғанда f(x) және φ(х) функциялары шексіз аз шама немесе шексіз үлкен шамалар болса және х
а ұмтылғанда f(x) және φ(х) функциялары шексіз аз шама немесе шексіз үлкен шамалар болса және х а ұмтылғанда
а ұмтылғанда 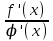
қатынастарының туындысы бар болса, онда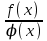 функциялары қатынасытарның шегі де бар болады және мына теңдік орындалады:
функциялары қатынасытарның шегі де бар болады және мына теңдік орындалады: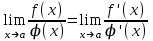 а=∞ болған жағдайда да осы ереже қолданылады.
а=∞ болған жағдайда да осы ереже қолданылады.
1-ескерту: ,
,  анықталмағандықтарын ашу үшін Лопиталь ережесін бірнеше рет қолдануға болады.
анықталмағандықтарын ашу үшін Лопиталь ережесін бірнеше рет қолдануға болады.
2-ескерту: Лопиталь ережесін қолданғанда қатынастарды түрлендіріп қысқартуға және шектерді есептеудің басқа да әдістеріне келтіруге болады.
Ұсынылатын әдебиеттер
1.Дүйсек А.К., Қасымбеков С.Қ. Жоғары математика. Алматы, 2004.
2.Ефимов Н.В. Краткий курс аналитической геометрии. М.: Наука, 1969.
3.Письменный Д. Конспект лекций по высшей математики. ч. 1., М.: Айрис пресс, 2004.
4.Лунгу К.Н. Сборник задач по высшей математики. 1 курс. М.: Айрис пресс, 2005.
СӨЖ-ге арналған бақылау тапсырмалары
ЖҮТ 6.1; ЖҮТ 6.2; ЖҮТ 6.3; [10, том 1, беттер 221-254]
Есептер АЗ-6.1; АЗ-6.2; АЗ-6.3; АЗ-6.4; АЗ-6.5; АЗ-6.6; [10, том 1]
8-тақырып. Функцияны оның туындысы арқылы зерттеу(2 сағ. )
Лекция жоспары:
1.Функцияның монотондық белгілері;
2. Функцияның экстремумының бар болуының жеткілікті шарттары. Қисықтың ойысты және дөңесті бөліктері. Иілу нүктелері. Қисықтың асимптоталары;
3. Функцияны зерттеу мен графигін салудың жалпы схемасы.
Лекцияның қысқаша мазмұны
Функцияның өсуі мен кемуі
Туындының қосымшаларының бірі оның функцияны зерттеуді, оның графигін салуда қолдану болып табылады.
Теорема. Егер интервалында дифференциалданатын
интервалында дифференциалданатын 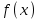 функциясы өсетін (кемитін) болса, онда
функциясы өсетін (кемитін) болса, онда 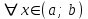 үшін
үшін 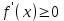 (
(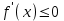 ).
).
Теорема. (жеткілікті шарт). Егер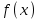 функциясы
функциясы 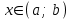 үшін
үшін  интервалында дифференциалданса және
интервалында дифференциалданса және 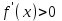 (
(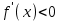 ) болса, онда осы функция
) болса, онда осы функция  интервалында өседі (кемиді).
интервалында өседі (кемиді).
Функцияның максимумы мен минимумы
Егер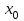 нүктесінің
нүктесінің 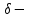 маңайы бар болып, осы маңайдың барлық
маңайы бар болып, осы маңайдың барлық 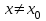 үшін
үшін 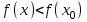 теңсіздігі орындалса,
теңсіздігі орындалса, 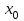 нүктесі
нүктесі  функциясының максимум нүктесі деп аталады.
функциясының максимум нүктесі деп аталады.
Максимум (минимум) нүктедегі функция мәні функцияның максимум (минимумы) деп аталады. Функцияның максимумы (минимумы) функцияның экстремумы деп аталады.
Экстремум ұғымы функцияның анықталу облысында жататын, нүктенің белгілі бір маңайымен байланысты. Сондықтан, функцияның анықталу облысының ішкі нүктесінде ғана экстремумы болуы мүмкін. Функция экстремумының бар болу шартын қарастырайық.
Теорема. (экстремумның қажетті шарты). Егер дифференциалданатын функциясының
дифференциалданатын функциясының  нүктесінде экстремумы бар болса, оның осы нүктедегі туындысы нөлге тең:
нүктесінде экстремумы бар болса, оның осы нүктедегі туындысы нөлге тең:  . Осылайша, үзіліссіз функцияның тек туындысы нөлге немесе туындысы болмайтын нүктелерінде ғана экстремумы болады. Осындай нүктелерді күдікті нүктелер деп атайды.
. Осылайша, үзіліссіз функцияның тек туындысы нөлге немесе туындысы болмайтын нүктелерінде ғана экстремумы болады. Осындай нүктелерді күдікті нүктелер деп атайды.
Теорема 25.9. (экстремумның жеткілікті шарты). Егер функциясы
функциясы  күдікті нүктесінің қандай да
күдікті нүктесінің қандай да  маңайында дифференциалданатын болса, және одан өткенде (солдан оңға)
маңайында дифференциалданатын болса, және одан өткенде (солдан оңға)  туындысы плюстен минусқа ауысса,
туындысы плюстен минусқа ауысса, 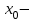 максимум нүкте, минустан плюске ауысса,
максимум нүкте, минустан плюске ауысса, 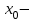 минимум нүкте.
минимум нүкте.
Теорема 25.10. Егер нүктесінде
нүктесінде  функциясының бірінші туындысы нөлге тең
функциясының бірінші туындысы нөлге тең 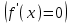 , ал
, ал  нүктесіндегі екінші туындысы бар болса, және нөлге тең болмаса
нүктесіндегі екінші туындысы бар болса, және нөлге тең болмаса 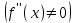 , онда
, онда 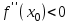 болғанда
болғанда  нүктесінде функция максимумға ие, ал
нүктесінде функция максимумға ие, ал 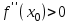 болғанда минимумға ие.
болғанда минимумға ие.
Функция графигінің дөңестігі, иілу нүктелері
Параметрлік түрде берілген функция
 аргументі мен
аргументі мен 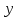 функциясы арасындағы байланыс параметрлік түрде екі теңдеу түрінде берілген болсын:
функциясы арасындағы байланыс параметрлік түрде екі теңдеу түрінде берілген болсын: 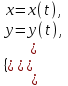 мұндағы
мұндағы  параметр деп аталатын көмекші айнымалы. функциясының туындысы бар деп алып және
параметр деп аталатын көмекші айнымалы. функциясының туындысы бар деп алып және 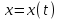 функциясының кері
функциясының кері 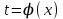 функциясы бар деп алып,
функциясы бар деп алып, 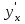 туындысын табайық. Кері функцияны дифференциалдау ережесі бойынша
туындысын табайық. Кері функцияны дифференциалдау ережесі бойынша 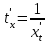 параметрлік түрде берілген
параметрлік түрде берілген  функциясын
функциясын 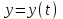 , мұндағы
, мұндағы 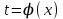 болатын күрделі функция түрінде қарастыруға болады.
болатын күрделі функция түрінде қарастыруға болады. Туындыны табу үшін бірқатар жағдайларда, алдымен берілген функцияны логарифмдейді. Кейіннен, алынған нәтижені дифференциалдайды. Осылай орындалған амалды – логарифмдік дифференциалдау деп аталады. Туындысы тек логарифмдік дифференциалдау арқылы табылатын функциялар бар. Солардың бірі
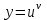 дәреже-көрсеткіштік функциясы, мұндағы
дәреже-көрсеткіштік функциясы, мұндағы 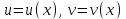 функциялары
функциялары  бойынша дифференциалданатын функциялар. Осы функцияның туындысын табайық:
бойынша дифференциалданатын функциялар. Осы функцияның туындысын табайық: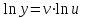 ,
, 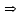
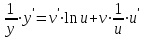 ,
, 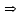
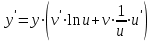 ,яғни
,яғни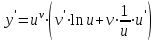 ,
, 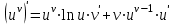 формуласын есте сақтау ережесін тұжырымдайық: дәреже – көрсеткіштік функцияның туындысы
формуласын есте сақтау ережесін тұжырымдайық: дәреже – көрсеткіштік функцияның туындысы 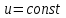
болғандағы көрсеткіштік функцияның туындысы мен
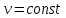 болғандағы дәрежелік функцияның туындысының қосындысына тең.
болғандағы дәрежелік функцияның туындысының қосындысына тең.  функциясының
функциясының 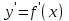 туындысы
туындысы 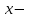 тан тәуелді функция да болып табылады, және бірінші ретті туынды деп аталады. Егер
тан тәуелді функция да болып табылады, және бірінші ретті туынды деп аталады. Егер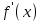 функциясы дифференциал-данатын болса, онда оның туындысы екінші ретті туынды деп аталып,
функциясы дифференциал-данатын болса, онда оның туындысы екінші ретті туынды деп аталып,  арқылы белгіленеді. Сонымен,
арқылы белгіленеді. Сонымен, 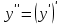 .Екінші ретті туындыдан алынған туынды бар болса, онда ол үшінші ретті туынды деп аталып,
.Екінші ретті туындыдан алынған туынды бар болса, онда ол үшінші ретті туынды деп аталып, 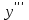 (немесе
(немесе 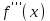 ,
, 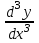 , ...) арқылы белгіленеді. Сонымен,
, ...) арқылы белгіленеді. Сонымен, 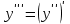 .
. 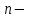 ретті туынды деп
ретті туынды деп 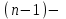 ретті туындыдан алынған туынды аталады:
ретті туындыдан алынған туынды аталады: 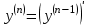 .
.Анықталмағандықтарды ашу.
 ,
,  анықталмағандықтарын ашудың тәсілдерінің бірі Лопиталь ережесі болып табылады және ол келесі теоремада негізделген.
анықталмағандықтарын ашудың тәсілдерінің бірі Лопиталь ережесі болып табылады және ол келесі теоремада негізделген.Теорема:f(x) және φ(х) функциялары х=а нүктесінен басқа х=а нүктесінің маңайындағы нүктелерде дифференциалданатын және анықталған болсын және φ
 (x)≠0 болсын. Егер х
(x)≠0 болсын. Егер х а ұмтылғанда f(x) және φ(х) функциялары шексіз аз шама немесе шексіз үлкен шамалар болса және х
а ұмтылғанда f(x) және φ(х) функциялары шексіз аз шама немесе шексіз үлкен шамалар болса және х а ұмтылғанда
а ұмтылғанда 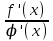
қатынастарының туындысы бар болса, онда
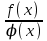 функциялары қатынасытарның шегі де бар болады және мына теңдік орындалады:
функциялары қатынасытарның шегі де бар болады және мына теңдік орындалады: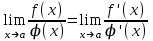 а=∞ болған жағдайда да осы ереже қолданылады.
а=∞ болған жағдайда да осы ереже қолданылады.1-ескерту:
 ,
,  анықталмағандықтарын ашу үшін Лопиталь ережесін бірнеше рет қолдануға болады.
анықталмағандықтарын ашу үшін Лопиталь ережесін бірнеше рет қолдануға болады.2-ескерту: Лопиталь ережесін қолданғанда қатынастарды түрлендіріп қысқартуға және шектерді есептеудің басқа да әдістеріне келтіруге болады.
Ұсынылатын әдебиеттер
1.Дүйсек А.К., Қасымбеков С.Қ. Жоғары математика. Алматы, 2004.
2.Ефимов Н.В. Краткий курс аналитической геометрии. М.: Наука, 1969.
3.Письменный Д. Конспект лекций по высшей математики. ч. 1., М.: Айрис пресс, 2004.
4.Лунгу К.Н. Сборник задач по высшей математики. 1 курс. М.: Айрис пресс, 2005.
СӨЖ-ге арналған бақылау тапсырмалары
ЖҮТ 6.1; ЖҮТ 6.2; ЖҮТ 6.3; [10, том 1, беттер 221-254]
Есептер АЗ-6.1; АЗ-6.2; АЗ-6.3; АЗ-6.4; АЗ-6.5; АЗ-6.6; [10, том 1]
8-тақырып. Функцияны оның туындысы арқылы зерттеу(2 сағ. )
Лекция жоспары:
1.Функцияның монотондық белгілері;
2. Функцияның экстремумының бар болуының жеткілікті шарттары. Қисықтың ойысты және дөңесті бөліктері. Иілу нүктелері. Қисықтың асимптоталары;
3. Функцияны зерттеу мен графигін салудың жалпы схемасы.
Лекцияның қысқаша мазмұны
Функцияның өсуі мен кемуі
Туындының қосымшаларының бірі оның функцияны зерттеуді, оның графигін салуда қолдану болып табылады.
Теорема. Егер
 интервалында дифференциалданатын
интервалында дифференциалданатын 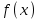 функциясы өсетін (кемитін) болса, онда
функциясы өсетін (кемитін) болса, онда 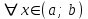 үшін
үшін 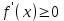 (
(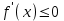 ).
).Теорема. (жеткілікті шарт). Егер
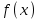 функциясы
функциясы 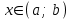 үшін
үшін  интервалында дифференциалданса және
интервалында дифференциалданса және 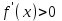 (
(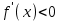 ) болса, онда осы функция
) болса, онда осы функция  интервалында өседі (кемиді).
интервалында өседі (кемиді).Функцияның максимумы мен минимумы
Егер
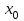 нүктесінің
нүктесінің 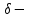 маңайы бар болып, осы маңайдың барлық
маңайы бар болып, осы маңайдың барлық 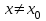 үшін
үшін 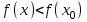 теңсіздігі орындалса,
теңсіздігі орындалса, 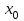 нүктесі
нүктесі  функциясының максимум нүктесі деп аталады.
функциясының максимум нүктесі деп аталады. 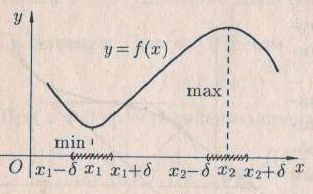 | Функцияның максимум нүктесі де осылай анықталады: егер 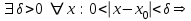 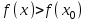 болса, болса, 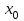 функциясының минимум нүктесі. 146-суретте функциясының минимум нүктесі. 146-суретте 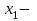 минимум нүктесі, минимум нүктесі, 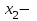  функциясының максимум нүктесі. функциясының максимум нүктесі. |
Максимум (минимум) нүктедегі функция мәні функцияның максимум (минимумы) деп аталады. Функцияның максимумы (минимумы) функцияның экстремумы деп аталады.
Экстремум ұғымы функцияның анықталу облысында жататын, нүктенің белгілі бір маңайымен байланысты. Сондықтан, функцияның анықталу облысының ішкі нүктесінде ғана экстремумы болуы мүмкін. Функция экстремумының бар болу шартын қарастырайық.
Теорема. (экстремумның қажетті шарты). Егер
 дифференциалданатын функциясының
дифференциалданатын функциясының  нүктесінде экстремумы бар болса, оның осы нүктедегі туындысы нөлге тең:
нүктесінде экстремумы бар болса, оның осы нүктедегі туындысы нөлге тең:  . Осылайша, үзіліссіз функцияның тек туындысы нөлге немесе туындысы болмайтын нүктелерінде ғана экстремумы болады. Осындай нүктелерді күдікті нүктелер деп атайды.
. Осылайша, үзіліссіз функцияның тек туындысы нөлге немесе туындысы болмайтын нүктелерінде ғана экстремумы болады. Осындай нүктелерді күдікті нүктелер деп атайды. Теорема 25.9. (экстремумның жеткілікті шарты). Егер
 функциясы
функциясы  күдікті нүктесінің қандай да
күдікті нүктесінің қандай да  маңайында дифференциалданатын болса, және одан өткенде (солдан оңға)
маңайында дифференциалданатын болса, және одан өткенде (солдан оңға)  туындысы плюстен минусқа ауысса,
туындысы плюстен минусқа ауысса, 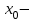 максимум нүкте, минустан плюске ауысса,
максимум нүкте, минустан плюске ауысса, 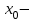 минимум нүкте.
минимум нүкте.Теорема 25.10. Егер
 нүктесінде
нүктесінде  функциясының бірінші туындысы нөлге тең
функциясының бірінші туындысы нөлге тең 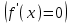 , ал
, ал  нүктесіндегі екінші туындысы бар болса, және нөлге тең болмаса
нүктесіндегі екінші туындысы бар болса, және нөлге тең болмаса 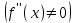 , онда
, онда 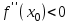 болғанда
болғанда  нүктесінде функция максимумға ие, ал
нүктесінде функция максимумға ие, ал 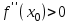 болғанда минимумға ие.
болғанда минимумға ие.Функция графигінің дөңестігі, иілу нүктелері