ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 33
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1'… b2'. Синдромные символы S1,S2, формируются по правилу: S1 = b1Åb1'; S2 = b2Åb2'. Следовательно, синдромный вектор или синдром Sί(x) в данном случае будет содержать два двоичных символа, т.е. S(x)= S1, S2.
12.а. Источник имеет следующие символы алфавита с их вероятностями появления:
Постройте кодовое дерево Хаффмана.
12.б. Запишите код Хаффмана.
Решение:
а) Алгоритм Хаффмана изящно реализует общую идею статистического кодирования с использованием префиксных множеств и работает следующим образом:
1. Выписываем в ряд все символы алфавита в порядке возрастания или убывания вероятности их появления в тексте.
2. Последовательно объединяем два символа с наименьшими вероятностями появления в новый составной символ, вероятность появления которого полагаем равной сумме вероятностей составляющих его символов. В конце концов построим дерево, каждый узел которого имеет суммарную вероятность всех узлов, находящихся ниже него.
3. Прослеживаем путь к каждому листу дерева, помечая направление к каждому узлу (например, направо - 1, налево - 0) . Полученная последовательность дает кодовое слово, соответствующее каждому символу.
Построим кодовое дерево для сообщения со следующим алфавитом:
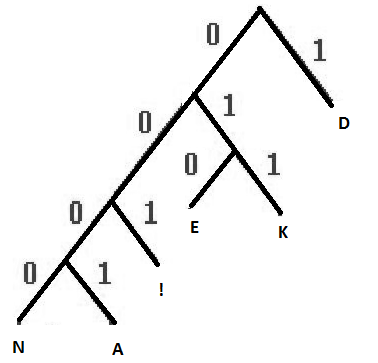
б) Запишем код Хаффмана.
12.а. Источник имеет следующие символы алфавита с их вероятностями появления:
| D | E | K | ! | A | N |
| 0,4 | 0,2 | 0,15 | 0,15 | 0,05 | 0,05 |
Постройте кодовое дерево Хаффмана.
12.б. Запишите код Хаффмана.
Решение:
а) Алгоритм Хаффмана изящно реализует общую идею статистического кодирования с использованием префиксных множеств и работает следующим образом:
1. Выписываем в ряд все символы алфавита в порядке возрастания или убывания вероятности их появления в тексте.
2. Последовательно объединяем два символа с наименьшими вероятностями появления в новый составной символ, вероятность появления которого полагаем равной сумме вероятностей составляющих его символов. В конце концов построим дерево, каждый узел которого имеет суммарную вероятность всех узлов, находящихся ниже него.
3. Прослеживаем путь к каждому листу дерева, помечая направление к каждому узлу (например, направо - 1, налево - 0) . Полученная последовательность дает кодовое слово, соответствующее каждому символу.
Построим кодовое дерево для сообщения со следующим алфавитом:
| символ | D | E | K | ! | A | N |
| вероятность | 0,4 | 0,2 | 0,15 | 0,15 | 0,05 | 0,05 |
| | D | E | K | ! | AN | |
| | 0,4 | 0,2 | 0,15 | 0,15 | 0,1 | |
| | D | !AN | E | K | | |
| | 0,4 | 0,25 | 0,2 | 0,15 | | |
| | D | EK | !AN | | | |
| | 0,4 | 0,35 | 0,25 | | | |
| | EK!AN | D | | | | |
| | 0,6 | 0,4 | | | | |
| | EK!AND | | | | | |

б) Запишем код Хаффмана.
| буква | код |
| D | 1 |
| E | 010 |
| K | 011 |
| ! | 001 |
| A | 0001 |
| N | 0000 |