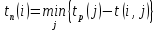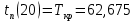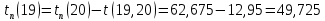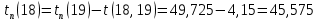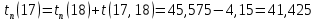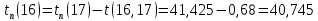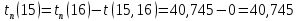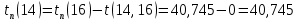Файл: Курсовая работа по дисциплине Математика Тема Математические методы и модели исследования операций.docx
Добавлен: 07.12.2023
Просмотров: 61
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
1.4 Выводы по решению задачи 1.5
Таким образом, для поставленной реальной задачи была составлена универсальная математическая модель, с помощью которой найдено решение, удовлетворяющее всем условиям задачи. Решение представляет собой план распределения производственной нагрузки между станками, использовав который конечная себестоимость продукции будет минимальна. В случае изменения начальных условий задачи, математическая модель может быть скорректирована и использована вновь.
-
Реферативный обзор научной статьи
ОПТИМАЛЬНОЕ УДЕРЖАНИЕ КОСМИЧЕСКОГО АППАРАТА С ДВИГАТЕЛЯМИ МАЛОЙ ТЯГИ НА СОЛНЕЧНО-СИНХРОННОЙ ОРБИТЕ
В статье “Оптимальное удержание космического аппарата с двигателями малой тяги на солнечно-синхронной орбите” Ван Лицзе и А.А. Баранов приводят методы и алгоритмы решения задач по формированию и поддержанию ССО при помощи химической двигательной установки(ХДУ) и электрических реактивных двигателей(ЭРД), которые решаются с помощью метода линейного программирования.
Актуальность данной статьи заключается в том, что ССО имеет большую значимость и интересна тем, что космический аппарат пролетает над одной и той же широтой земной поверхности приблизительно в одно и то же местное солнечное время, из-за чего угол освещения земной поверхности очень хорошо подходит для спутников дистанционного земного зондирования. Именно поэтому важно создать оптимальный и универсальный алгоритм корректировки эллиптических орбит космических аппаратов. На основе метода внутренних точек для решения задач ЛП разработан численный метод расчета оптимальных продолжительных маневров.
В статье «Решение задач оптимизации энергетических систем с несколькими автономными энергоустановками» И. Л. Майков, Л.Б. Директор и В.М. Зайченко приводят методы и алгоритмы решения задач по увеличению эффективности энергетических сетей, который позволит свести задачу оптимизации с несколькими автономными энергетическими установками к задаче линейного программирования.
Для лучшего понимания логики поддержания Солнечно-синхронной орбиты авторы приводят пример формирования и поддержания ССО при помощи ЭРД. Для описания орбитального движения используется геоцентрическая инерциальная система координат OXYZ. Затем выводится уравнение движения центра масс КА. Для решения сформулированной задачи используется теория дискретного терминального управления, и последующий переход к дискретной модели полета. Введя условия и ограничения, получим матрицу, после чего задача коррекции траектории сводится к задаче математического программирования, а именно к нахождению вектора минимизирующего линейный функционал (с ограничениями в виде векторных равенства и неравенства).
Такой подход справедлив для задачи с небольшой размерностью, однако с помощью алгоритма внутренних точек задача линейного программирования эффективно решается.
Для решения задачи использовалась итерационная процедура, далее авторами приведены таблицы и графики, иллюстрирующие наиболее эффективные режимы работы ЭРД
Основной результат применения оптимизационной задачи в решении исследуемой проблемы:
Обоснована постановка задачи математического программирования по формированию и поддержанию ССО
Предложена дискретная математическая модель движения КА, управляемого двигателями малой тяги, допускающая практическое применение при проектировании полетов КА на ССО.
А также разработан численный алгоритм расчета корректирующих импульсов для поддержания ССО, базирующийся на методах задач линейного программирования с ограничениями.
Данная статья опубликована авторами Ван Лицзе и А.А. Барановым в Научном вестнике Московского государственного технического университета имени Н.Э. Баумана в 2015 году.
Литература:
Московского государственного технического университета имени Н.Э. Баумана в 2015 году.
1. Чернов А.А., Чернявский Г.M. Орбиты спутников дистанционного зондирования Земли: Лекции и упражнения. М.: Радио и связь, 2004. 200 c.
2. Колосов Г.Е., Ван Лицзе. Коррекция параметров полета с двигателями малой тяги // Полет. Общероссийский научно-технический журнал. 2012. № 11. C. 27–36.
3. Бахшиян Б.Ц., Назиров Р.Р., Эльясберг П.Е. Определение и коррекция движения: Гарантирующий подход. М.: Наука, 1980. 360 c.
4. Назиров Р.Р., Тимохова Т.А. Оптимальная линейная коррекция эллиптических
орбит // Автоматика и телемеханика. 1993. № 3. С. 93–101.
5. Улыбышев Ю.П. Оптимизация многорежимных траекторий сближения с ограничениями // Космические исследования. 2008. Т. 46. № 2. С. 135–147.
6. Баранов А.А., Де Прадо А.Ф.Б., Разумный В.Ю., Баранов А.А. Оптимальные переходы с малой тягой между близкими околокруговыми компланарными орбитами // Космические исследования. 2011. Т. 49. № 3. С. 278–288.
-
Управление комплексом технологических работ методами сетевого планирования и управления
Монтаж ленточного конвейера
-
Условия и постановка задачи
Для соответствующих варианта и типа задачи в таблице задан комплекс работ. Необходимо:
1)определить ожидаемое время выполнения работы;
2)постройте структурный сетевой график. При необходимости корректно установить нумерацию работ и событий;
3)определить основные характеристики сетевого плана. Рассчитать наиболее ранние и наиболее поздние сроки наступления событий; найти критический путь и критическое время Tкр; определить полные и независимые резервы всех работ, коэффициенты напряженности некритических дуг.
4)провести оптимизацию сетевого плана по критерию «стоимость», т.е. без уменьшения критического времени реализации плана проекта минимизировать общую стоимость работ. Выполнить оптимизацию составив и решив с использованием Microsoft Excel задачу линейного программирования. Предложить способ графического отображения результатов оптимизации сетевого плана и реализовать его.
5)провести оптимизацию сетевого плана по критерию «время», т.е. без уменьшения общей стоимости проекта минимизировать время его реализации. Выполнить оптимизацию, составив и решив с использованием Microsoft Excel задачу линейного программирования.
6)провести оптимизацию сетевого плана по критерию «время – стоимость». Выполнить оптимизацию, составив и решив с использованием Microsoft Excel задачу линейного программирования. Рассмотреть случаи
Tдир=0,9Tкр;Tдир=0,85Tкр;Tдир=0,8Tкр. При вычислении Tдир применять округление с избытком до целых.
3.2 Построение сетевой модели
Для решения поставленной задачи составим математическую модель. Модель представляет из себя сетевой план, который состоит из 20 событий и 28 работ, и ограничений, поставленных в условии задачи.
Для начала построим сетевой график и проведём корректировку шифров работ. Затем, основываясь на входных данных для задачи, а именно минимальное и максимальное время выполнения работы, вычислю ожидаемое
(среднее) время работы.
Таблица 12 – Входные данные для задачи
| № | Работы | Время выполнения работы | Общая стоимость, усл.ед | Маржинальная стоимость, усл.ед | |||
| Исходный шифр | После корректировки | tmin | tmax | tож | |||
| 1 | (0,1) | (0, 1) | 4,8 | 8,1 | 6,45 | 33 | 1,6 |
| 2 | (0, 2) | (0, 2) | 3,8 | 7,1 | 5,45 | 16,6 | 1,74 |
| 3 | (1, 3) | (1, 3) | 0 | 0 | 0 | 0 | -- |
| 4 | (1, 6) | (1, 6) | 4,3 | 7,6 | 5,95 | 27 | 2,7 |
| 5 | (2, 3) | (2, 3) | 13,3 | 17,1 | 15,2 | 1037 | 23 |
| 6 | (3, 4) | (3, 4) | 3,3 | 6,1 | 4,7 | 71 | 5,3 |
| 7 | (3, 5) | (3, 5) | 2,8 | 6,1 | 4,45 | 18 | 3,6 |
| 8 | (3, 6) | (3, 6) | 3,3 | 4,6 | 3,95 | 12,25 | 2,3 |
| 9 | (4, 6) | (4, 6) | 0,33 | 0,66 | 0,495 | 7,6 | 1,65 |
| 10 | (5, 6) | (5, 6) | 0,33 | 0,56 | 0,445 | 4,3 | 0,85 |
| 11 | (6, 7) | (6, 7) | 0,73 | 0,96 | 0,845 | 15,7 | 1,75 |
| 12 | (6, 8) | (6, 11) | 0,53 | 0,73 | 0,63 | 12,7 | 1,45 |
| 13 | (6, 9) | (6, 8) | 0,63 | 0,86 | 0,745 | 14,6 | 1,75 |
| 14 | (6, 10) | (6, 9) | 5,3 | 7,6 | 6,45 | 92 | 2,8 |
| 15 | (6, 11) | (6, 10) | 6,3 | 9,6 | 7,95 | 259 | 3,4 |
| 16 | (7, 8) | (7, 11) | 0 | 0 | 0 | 0 | -- |
| 17 | (8, 12) | (11, 14) | 0,93 | 1,13 | 1,03 | 7,4 | 4,4 |
| 18 | (9, 13) | (8, 12) | 0,63 | 0,83 | 0,73 | 10,9 | 2,8 |
| 19 | (10, 14) | (9, 13) | 6,3 | 10,6 | 8,45 | 88,6 | 4 |
| 20 | (11, 15) | (10, 16) | 3,65 | 6,26 | 4,955 | 56,4 | 6,8 |
| 21 | (13, 16) | (12, 15) | 2,65 | 5,26 | 3,955 | 24,2 | 2,4 |
| 22 | (12, 15) | (14, 16) | 0 | 0 | 0 | 0 | -- |
| 23 | (14, 15) | (13, 16) | 0 | 0 | 0 | 0 | -- |
| 24 | (16, 15) | (15, 16) | 0 | 0 | 0 | 0 | -- |
| 25 | (15, 17) | (16, 17) | 0,63 | 0,73 | 0,68 | 18,4 | 2,8 |
| 26 | (17, 18) | (17, 18) | 3,65 | 4,65 | 4,15 | 26,4 | 4 |
| 27 | (18, 19) | (18, 19) | 3,65 | 4,65 | 4,15 | 20,5 | 1 |
| 28 | (19, 20) | (19, 20) | 11,3 | 14,6 | 12,95 | 431 | 12,8 |
-
Вычислю ранние сроки свершения событий:
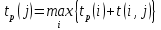
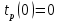
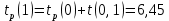
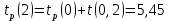
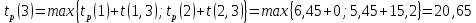
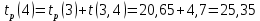
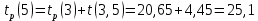
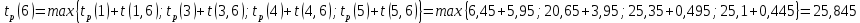
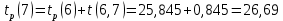
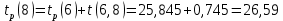
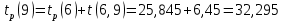
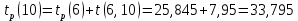
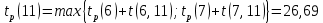
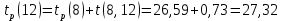
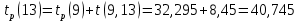
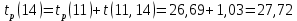
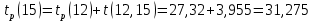
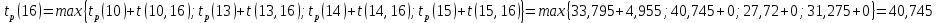
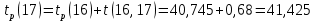
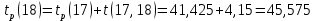
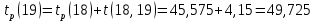
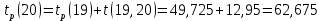
-
Определю критический путь, он будет равен раннему времени свершения последнего события:
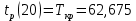
-
Найдём поздние сроки свершения событий: